Bonjour robby

Sens direct: s'ils sont colinéaires, u écris que a'=a et b'=b et tu calcules.

Pour la réciproque: si les 4 coordonnées sont nulles, on a v=v'=0. Sinon, il y a bien une des coordonnées qui est non nulle par exemple a.

Alors de a'=a(a'/a) et de ab'=a'b, tu tires b'=b(a'/a)

merci Camélia

Bonjour,

on peut aussi démontrer ça de manière géométrique en utilisant le théorème de Thalès.

Personnellement, j'aime bien le montrer ainsi, pour que les élèves voient que c'est quelque chose de connu mais écrit sous une autre forme.

quand tu auras un peu de temps,je veux bien voir ça aussi s'il te plait

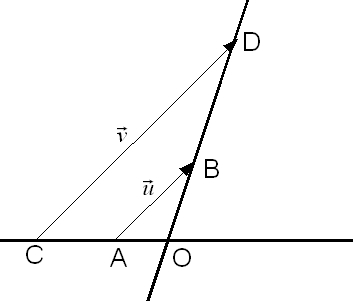
Voilà une petite image vite fait.

Tu prend un repère quelconque d'origine O. (car la formule de colinéarité de vecteurs marche dans tout repère).
Et tu places les deux vecteurs u et v par exemple comme ceci.

Les coordonnées des vecteurs sont données par les longueurs OA, OB, OC et OD.

Un petit coup de Thalès et sa réciproque permet de montrer facilement l'égalité que les droites (AB) et (CD) sont parallèles si et seulement si OA/OC=OB/OD, ce qui revient à x'y-xy'=0.

Attention, il faut traiter à part les cas particuliers où les vecteurs sont parallèles aux axes du repère, mais ça se traite vite fait.

Une autre approche consiste à utiliser les triangles semblables, c'est le même principe !

Super!
Merci Jamo!