Inscription / Connexion Nouveau Sujet
probabilité
Bonsoir
je vous propose l'exercice suivant ;
on se donne les les lettres de l'alphabet A,B,....,Z et on effectue des tirages aléatoires ave remise d'une lettre à la fois ( on note les lettres tirées ) et on arrête les tirages lorsqu'on obtient pour la premiere fois toutes les lettres du mot "MATH", si on note X la variable aléatoire égale au rang pour lequel on obtient pour la premiere fois toutes les lettres du mot "MATH" , quelle est la loi de X et son esperance ?
27,0833...
Bonjour,
Avec remise signifie que l'ordre des tirages n'a pas d'importance.
Si on tire AHMT on a bon...
Cliquez pour afficherBonjour
dans son premier message, Verdurin a indiqué la bonne espérance de la variable X (à savoir 325/6 )
Quant à la loi de probabilité suivie par X, c'est un peu plus compliqué :
pour tout
Par ailleurs, un grand spécialiste illogique pose sa question : "où intervient la théorie des probabilités ?"
Ce serait risible si elle ne montrait pas à quel point il a perdu toute compréhension des mathématiques et des probabilités.
Est-ce la fonction de masse de notre variable peut-être approchée par une loi normale ou une loi exponentielle ?
Un petit dessin :
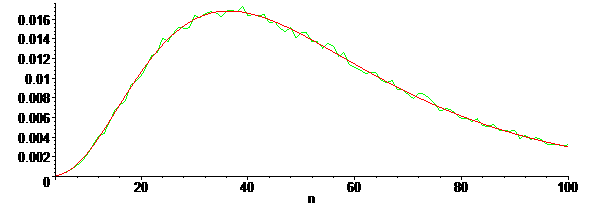
Non, cela ne ressemble pas du tout à une loi normale. Ni même à une loi exponentielle...
Bonsoir,
je suis d'accord avec les résultats donnés par leon1789.
On peut généraliser avec un alphabet de N lettres et un mot de p lettres.
La loi de probabilité de la variable X est donnée par :
Cliquez pour afficherL'espérance vaut
Cliquez pour afficherLa variance vaut
Cliquez pour afficherok Jandri ! 
Même question avec le mots PROBABILITES
Attention, il y a plusieurs fois les mêmes lettres
Je pense que la formule donnant P(X=n) est une somme dont les termes sont des produits du type :
(.../26)^n * polynôme en n (de degré 0 ou 1 ou 2)
J'ai une fomule pour l'espérance dans le cas "PROBABILITES". Le résultat que j'ai donné vient de cette formule.
Bon, j'ai bien une formule de P(X=n) pour le mot PROBABILITES.
En particulier, son espérance est ,
très proche de 90.15 en effet.
P(X=n)
= (25/26)^n *(198/625+2/625*n)
+(24/26)^n *(-10165/3456-15/256*n-1/6912*n^2)
+(23/26)^n *(147800/12167+4528/12167*n+24/12167*n^2)
+(22/26)^n *(-38990/1331-1652/1331*n-14/1331*n^2)
+(21/26)^n *(60140/1323+1108/441*n+40/1323*n^2)
+(16/26)^n *(-445/1024-129/2048*n-5/2048*n^2)
+(20/26)^n *(-1883/40-1309/400*n-21/400*n^2)
+(19/26)^n *(223160/6859+19040/6859*n+392/6859*n^2)
+(18/26)^n *(-10550/729-362/243*n-28/729*n^2)
+(17/26)^n *(18470/4913+2266/4913*n+72/4913*n^2)
Bref, une formule d'ordinateur !
le terme +(16/26)^n *(-445/1024-129/2048*n-5/2048*n^2)
s'est intercalé en plus milieu ! dommage pour la présentation.
Bonjour,
j'ai aussi une formule que j'établis par récurrence.
Je note l'espérance de
égale au nombre de tirages pour obtenir pour la première fois les lettres d'un mot formé avec
lettres dont
sont répétées deux fois, les
autres une seule fois (pour PROBABILITE on a
et
) pour un alphabet de
lettres.
Pour ,
et
on obtient
Je ne suis pas allé jusqu'à !
Je vois par ailleurs que notre grand illogique considère B et B comme deux lettres différentes, idem pour I et I... donc dans un alphabet à 28 lettres ? Bref, il fait "comme il veut dans son mode (quasi) réel".
Apparemment, il semble que les solutions proposées sont assez divergentes, mais c'est normal, puisque chacun peut interpréter l'énoncé différemment.
Bonjour,
visiblement notre Dunning Kruger mathophobe n'a jamais compris que plusieurs personnes peuvent avoir des angles de réflexion différents sur une même question, et pour autant y apporter des réponses... qui coïncident heureusement ! Cela fait partie de la beauté de la réflexion à plusieurs et des échanges d'idées complémentaires.
cet énoncé n'a d'intérêt que parce qu'il s'agit du premier succès après des échecs.
Ben non, ce n'est pas le premier succès. Encore une fois, Dunning Kruger n'arrive pas à formaliser : il s'agit d'une recherche du "rang" du n-ième succès (avec des probabilités des succès différentes au fil des succès passés...).
C'est pour cela que la loi de probabilité suivie n'est pas aussi simple qu'une seule loi géométrique, comme l'a indiqué Verdurin dès la première réponse.
Oui, moi, je suis pas prof, alors je réfléchi.
Réfléchis encore, tu as encore du chemin à faire...
quand il y a des exercices un peu tordus le seule chose que je sache faire est d'écrire une simulation.
D'une part, l'exercice n'est pas tordu. Simplement, Dunning Kruger n'a pas compris la question posée.
Par ailleurs, notre mathophobe n'est pas aussi expert en proba qu'il aime le clamer. On le savait bien... Mais alors comment se permet-il de calomnier tous les matheux ? c'est une honte.
Et pour faire une simulation utile, encore faut-il comprendre le problème. On lui répète pourtant à chaque fois, ça pêche puisqu'il ne comprend pas la question posée. En plus, ses résultats sont incohérents avec son code source... bref, la totale, comme d'hab.
Annuler
connectez vous