bonsoir,

résoudre f(x)=3,6 et g(x)=3,6

utiliser la fonction exponentielle pour faire partir les logarithmes.

Salut

Voilà un problème:
Un promoteur envisage de commercialiser un programme de contruction d'immeubles.

> Le projet P1:
le coût de production de n immeubles est donné en millions d'euros (M€) par
f(x)=ln(3.2x+1)
> Le projet P2:
le coût de production de n immeubles est donné en millions d'euros (M€) par
g(x)=ln(0.4x²+1)

Déterminer le nb maximum d'immeubles dt on peut envisager la production pr chacun des projets si le coût de production est limité à 3.6 M€.

J'ai trouvé graphiment:
> Pr P1: 11 immeubles
> Pr P2: 10 immeubles

Mais comment le démontrer par le calcul ??

*** message déplacé ***

Bonjour.

*** message déplacé ***

ln(3.2x+1)<=3.6
3.2x+1<=exp(3.6)
x<=[exp(3.6)-1]/(3.2)
A+

*** message déplacé ***

Oui ça je sais ^^ mais le problème c'est que je trouve pas 10 ou 11 !!

Salut,

f(x)=ln(3.2x+1)=3.6
<=> 3.2x+1=e^3.6
<=> 3.2x=e^3.6-1
<=> x = (e^3.6-1)/3.2
<=> x 11.12

g(x)=ln(0.4x²+1)=3.6
<=> 0.4x²+1=e^3.6
<=> x²=(e^3.6-1)/0.4
<=> x² 10.47
==> tu es sûr que c'est x² et non x ?

Pookette

Oui s'était x² mais c'est bon j'ai trouvé la réponse enfin...... ^^

Voilà un problème:
Un promoteur envisage de commercialiser un programme de contruction d'immeubles.

> Le projet P1:
le coût de production de n immeubles est donné en millions d'euros (M€) par
f(x)=ln(3.2n+1)
> Le projet P2:
le coût de production de n immeubles est donné en millions d'euros (M€) par
g(x)=ln(0.4n²+1)

Pr chaque projet, le bénéfice réalisable par le promoteur est égal, pour les ventes de n immeubles, au chiffre d'affaires diminué du coût de production.

a) Exprimer en fonction de n les bénéfices B1(n) et B2(n) réalisables avec respectivement les projets P1 et P2

*** message déplacé ***

bonjour

quelle est l'expression du chiffre d'affaire ?

Philoux

*** message déplacé ***

Oups j'ai oublié une partie de l'énnoncé désolée... :/

Dans les 2 cas le prix de vente envisagé pour un immeuble est de 500 000 €, soit 0.5 M€. Le chiffre d'affaires prévisible pour les ventes de n immeubles est donc h(n)=0.5n.

*** message déplacé ***

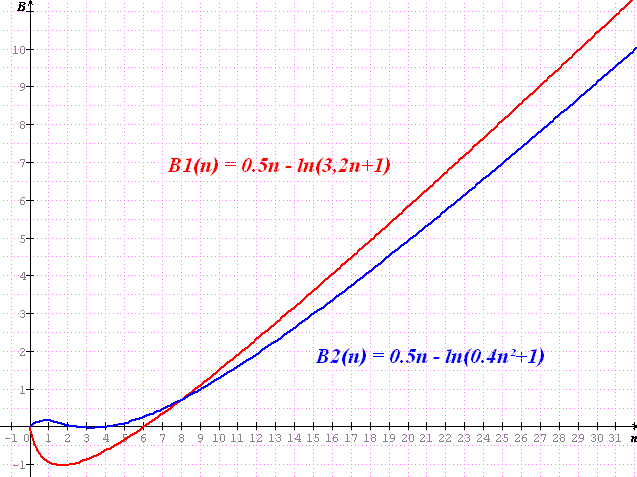
B1(n)= 0.5n - ln(3.2n+1)

B2(n)= 0.5n - ln(0.4n²+1)

fais l'etude de ces fonction dérivées...

Philoux



*** message déplacé ***

ils te demanderont à partir de combien d'immeuble tel projet est-il plus rentable qu'un autre

regardes en n=8...

à démontrer analytiquement cependant

Philoux

*** message déplacé ***