salut

je suppose que les points A, B et C sont distincts et non alignés...

ils définissent donc un plan P et (A, AB, AC) est un repère de ce plan

je note alors n un vecteur normal (et unitaire) à ce plan

alors pour tout point M il existe des réels x, y et z tels que

PS: tu peux même choisir des vecteurs i et j tels que   et  

La suite alors stp

Bonjour,

Peut-être serait-il utile de considérer la hauteur issue de A dans le triangle ABC

Bonjour,

Que se passe-t-il si est sur la droite ?
Ensuite, On peut s'intéresser au cas où n'est pas sur cette droite, et donc et ont un produit vectoriel non nul.

bonjour,
Dans le cas général, en supposant A,B,C non alignés, il est nécessaire que soit colinéaire à , il semble alors évident que M est le sommet d'un tétraèdre trirectangle de base (ABC), ainsi M est à l'intersection de 3 surfaces que je te laisse deviner

Excuse moi GBZM, je n'avais pas vu que tu relançais la question, pas plus que l'aide de Larrech .
à ce  propos on peut indifféremment choisir la hauteur issue de C ou de B dans le triangle ABC

DOMOREA, j'ai bien l'impression que tu induis le questionneur en erreur.

Je ne voyais pas un tétraèdre trirectangle, mais plus modestement bi.

Bonsoir cher tous je lis les réponses mais au finish je ne sais vraiment ce qu'il fait retenir à la fin

Ne peux-tu pas répondre à ma question ? Que se passe-t-il si est sur la droite ?

Pour compléter
J'ai mis à l'écart les cas évidents où l'un des membres ou était nul.
cela , je pense que madiba aurait pu le découvrir si elle connait le produit vectoriel dans son interprétation géométrique

Ce qui fournit une infinité de solutions (c'est le sens de "dans le cas général",(expression malheureuse je l'avoue).
Mais pour ce que j'ai proposé, il me semble bien sauf erreur que cela donne 2  solutions isolées pour M en dehors des solutions déjà trouvées (précision apportée à cause du cas où le triangle ABC est rectangle en A, B ou C). les surfaces dont j'ai parlé sont évidement des sphères.

Pour madiba Intuitivement: Soient 3 demie-droites de même origine M perpendiculaires  deux à deux, on peut ajuster ce système de manière à ce que chacune d'entre elles possède distinctement un unique point parmi A,B ou C

DOMOREA, tu persistes dans l'erreur. Il n'y a aucune raison pour que (MB) soit perpendiculaire à (MC).

en effet, tu as raison
(MA) orthogonal au plan (MBC) suffit, je ne vois pas pourquoi je me suis arrêté à ce cas particulier et donc 2 sphères suffisent.

Bonjour à tous,

Je ne pense pas dévoiler grand chose avec cette épure animée où les points sont dans un plan horizontal et où figurent les projections de l'ensemble cherché en rouge.

Juste pour le "fun" :

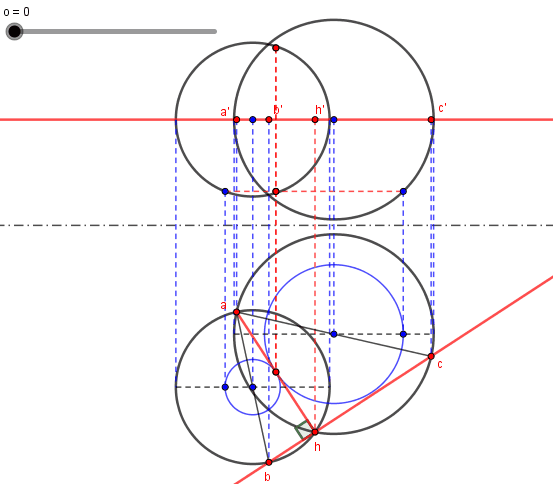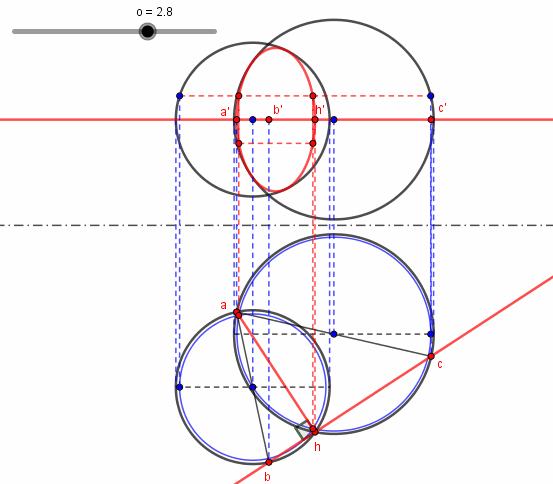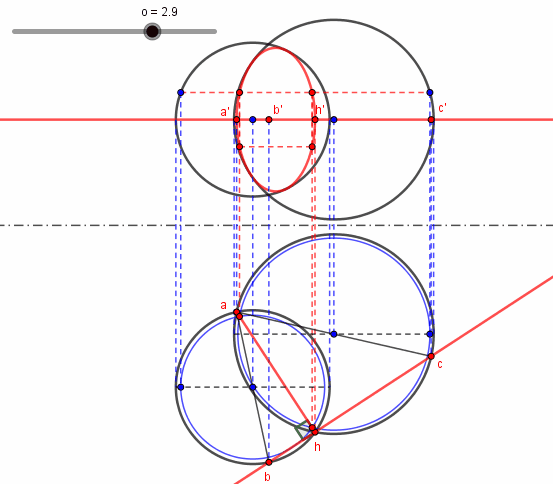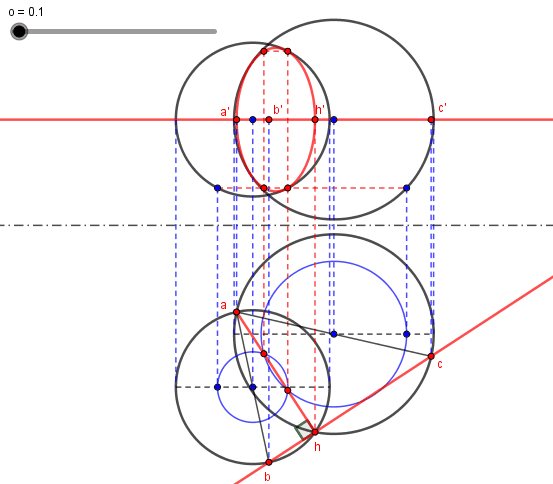
Le diable se cache souvent dans les cas particuliers.

Une question à madiba :

Que se passe-t-il lorsque les points sont alignés ?

L'ensemble chercher est la droite (AB)

L'ensemble chercher est la droite (AB)

Bonsoir madiba,

Je crois que tu n'as pas bien apprécié les différentes réponses :

  Que la droite (et non pas la droite comme tu sembles le suggérer) , fasse partie de l'ensemble cherché, personne ne le conteste.

Mais pas que : il y a aussi l'intersection de deux sphères de diamètres et qui est en général un cercle de l'espace.

Relis attentivement tout ce qui a été écrit.

Ah! Je n'avais pas compris le message de 21h22 comme une réponse à 14h57.

Bonsoir,

Voici une autre façon de chercher les solutions:


Cas 1)
Cas 2) ; posons : (donc ); avec :;

Décomposons :

; (si , on choisi vecteur orthonormal à )
;



Soient:



Donc:


Donc, ceci revient à résoudre le système suivant (qui est facile à résoudre):
    Avec:

Une fois déterminés, on détermine les coordonnées de à partir de l'expression suivante:

Il reste à résoudre le système,

salut Razes : c'est en gros ce que je proposais dès mon premier msg :

distinguer les cas particuliers
prendre une base "adaptée" aux points A, B et C

sachant qu'on peut accélérer les choses lorsqu'on connait son cours ...

Bonjour,

Ces calculs sont assez pénibles, mais la résolution géométrique est simple.

oui bien sûr ...

mais on y tous passé car c'est un bon entrainement au calcul vectoriel "avec des formules", ensuite de montrer tout l'intérêt de s'approprier et maitriser les interprétations et propriétés géométriques qui permettent de substituer les idées au calcul (comme le disait Dirichlet)

Bonjour,
@GBZM, je suis d'accord que le calcul est pénible.

Je suis un adepte de la géométrie depuis mes années college (50 ans) et j'aurais aimé aider avec une solution courte et esthétique avec une interprétation géométrique.

Mais des fois on est obligé de passer par la géométrie analytique et se taper des calculs, et comme à dit carpediem que je salue, l'élève est censé connaître les différentes méthodes.

Mais rien n'empêche d'interpréter les résultats trouvés géométriquement.

@carpediem, effectivement le calcul est très rapproche de l'idée  que tu as propose qui est assez large donc difficile que les différentes façons soient disjointes.

Géométriquement, le plan (P) passant par A orthogonal à (BC) coupe cette droite en H, pied de la hauteur issue de A dans le triangle ABC.

Le lieu de M est  le cercle de diamètre AH dans le plan (P) (en plus de la droite (BC) elle-même).

_{sauf erreur}

Une "solution courte et esthétique avec une interprétation géométrique" a déjà été donnée pour l'essentiel. Je reprends  :

On suppose non alignés

Si est sur la droite , alors et la condition est vérifiée.

Sinon,   est un vecteur non nul orthogonal à et , donc si et seulement si est orthogonal à et , c.-à-d. si et seulement si appartient à l'intersection des sphères de diamètres et .
Cette intersection est le cercle passant par , contenu dans le plan orthogonal à et de centre le pied de la hauteur issue de dans le triangle .

Oups, le pied de la hauteur est bien sûr le point diamétralement opposé à , et pas le centre du cercle.