Niveau Master Maths

Projection orthogonale d'angle

Posté par
Rintaro 10-10-21 à 12:05

Bonjour,

je m'excuse par avance si je ne poste pas dans le bon fil, j'hésite avec l'espace "détente" car ça ne concerne pas mes cours mais plutôt un exercice que je trouve amusant dans le livre de Michel Audin sur la géométrie. L'exercice V.26 a pour objectif de montrer une relation vérifiée par les entiers du symbole de Schläfli d'un polyèdre convexe régulier, et pour cela l'auteur nous demande de démontrer une inégalité. Je ne recopie que la première question qui m'intéresse :

"Soient A, B et C trois points non alignés dans l'espace et P un plan contenant la droite (BC). On appelle a le projeté orthogonal de A sur P. En comparant les produits scalaires $\overset{\rightarrow}{AB} \cdot \overset{\rightarrow}{AC}$ et $\overset{\rightarrow}{aB} \cdot \overset{\rightarrow}{aC}$ , montrer que :

$\cos(\overset{\rightarrow}{AB},\overset{\rightarrow}{AC}) \geq \cos(\overset{\rightarrow}{aB},\overset{\rightarrow}{aC})$

et étudier le cas d'égalité."

Je précise ici que ce sont les cosinus de mesure d'angles géométriques définis par le produit scalaire. Je joins deux images d'une situation "non dégénérée" (où a n'est pas égal à B ou C par hasard), j'espère que ce sera visible et compréhensible.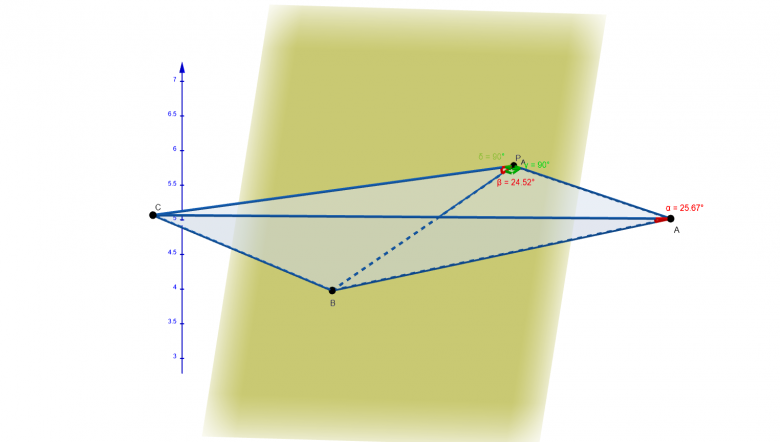

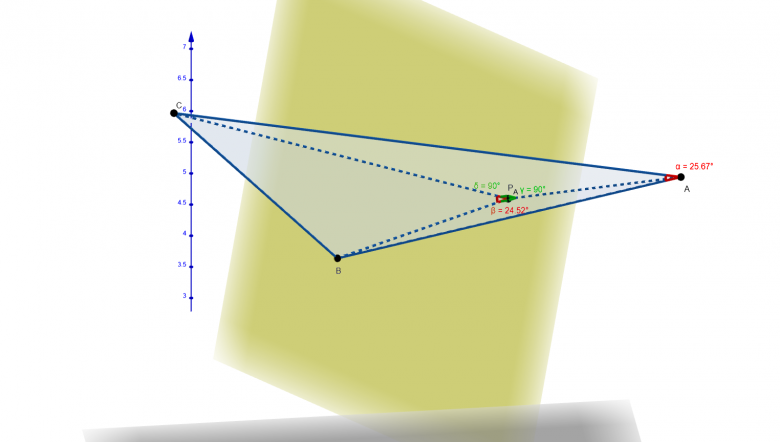
$Projection orthogonale d\'angle$

$Projection orthogonale d\'angle$

En utilisant les relations d'orthogonalité et la relation de Chasles, je trouve :

$\overset{\rightarrow}{AB} \cdot \overset{\rightarrow}{AC} = \|\overset{\rightarrow}{Aa}\|^2 + \overset{\rightarrow}{aB} \cdot \overset{\rightarrow}{aC}$

ce qui donne :

$\|\overset{\rightarrow}{AB}\| \| \overset{\rightarrow}{AC}\|\cos(\overset{\rightarrow}{AB}, \overset{\rightarrow}{AC}) = \| \overset{\rightarrow}{Aa}\|^2 + \|\overset{\rightarrow}{aB}\| \| \overset{\rightarrow}{aC}\|\cos(\overset{\rightarrow}{aB}, \overset{\rightarrow}{aC})$

J'ai fait des études de cas. J'ai réussi à montrer l'inégalité lorsque $\cos(\overset{\rightarrow}{AB}, \overset{\rightarrow}{AC}) \leq 0$ (je peux détailler si vous voulez), puis le cas facile où $\cos(\overset{\rightarrow}{AB}, \overset{\rightarrow}{AC}) > 0$ et $\cos(\overset{\rightarrow}{aB}, \overset{\rightarrow}{aC}) \leq 0$ .

Je bloque sur le dernier cas, à savoir $\cos(\overset{\rightarrow}{AB}, \overset{\rightarrow}{AC}) > 0$ et $\cos(\overset{\rightarrow}{aB}, \overset{\rightarrow}{aC}) > 0$ . Je n'arrive pas à montrer l'inégalité. J'ai tenté par l'absurde mais rien. J'ai aussi tenté d'utiliser que :

$\|\overset{\rightarrow}{AB}\| > \|\overset{\rightarrow}{aB}\| \\ \|\overset{\rightarrow}{AC}\| > \|\overset{\rightarrow}{aC}\| \\ \\ \|\overset{\rightarrow}{AB}\| \geq \|\overset{\rightarrow}{aA}\| \\ \|\overset{\rightarrow}{AC}\| > \|\overset{\rightarrow}{aA}\| ~~\text{par plus petite distance de A avec les points de P}$

mais rien non plus, j'ai l'impression de passer à côté de quelque chose d'évident. Pouvez-vous m'aider ?

Merci.

Posté par Projection orthogonale d'angle 10-10-21 à 17:12

bonjour,
Latex étant en panne, je suis désolé, je ne peux lire ton développement.

En revanche je te propose une solution très élémentaire qui est peut-être la tienne.

Excuses pour l'écriture en l'absence de Latex.

Je pose aB=cet aC=b
La projection orthogonale H de A sur BC est aussi la projection orthogonale de a sur BC (théorème des 3 perpendiculaires)

Soit x la distance Aa, considérons A variable sur la perpendiculaire au plan P passant par a, ce qui implique que les produits scalaires <BA.BC> et <CA.CB> sont des constantes k et k'.

Comme Les distances AB et AC sont des fonctions croissantes de x (pythagore), les angles ABC et ACB sont des fonctions croissantes de x tendant vers PI/2, en effet cos(ABC)=<BA.BC>/(BC.racine(x²+c²)) idem pour l'autre.

Il suffit de considérer leur cosinus respectifs, donc la mesure de l'angle BAC est une fonction décroissante de x.
(somme des angles d'un trngle)
comme pour Aa=x=0 quand A appartient au plan on a les deux angles confondus ...

Posté par re : Projection orthogonale d'angle 10-10-21 à 18:52

Bonsoir DOMOREA,

et désolé pour le temps de réponse. Merci beaucoup pour cette réponse, je m'en sortais absolument pas avec toutes mes inégalités ; votre preuve est incroyable, simple et intuitive avec des dessins.
Vous m'avez totalement dépanné, encore merci !

Bonne fin de soirée

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Fiches de mathématiques

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Projection orthogonale d'angle

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths