Inscription / Connexion Nouveau Sujet
Pythagore
Bonne nuit à tous
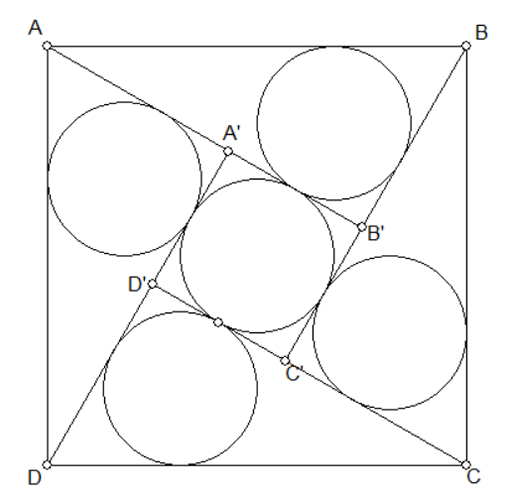
La figure ci-dessous montre une des multiples démonstrations du théorème de Pythagore dont la preuve se limite à dire:
Regarde.
Mais regardez-y d'un peu plus près: tous les cercles de la figure ont le même rayon.
Comment-est-ce possible?
Amicalement
pappus
Mon cher Malou
J'ai trouvé ce problème dans:
Japanese Temple Geometry Problems
San Gaku
Winnipeg, Canada 1989
H.Fukagawa & D.Pedoe
D.Pedoe est un mathématicien de renommée mondiale dont je m'étonne qu'il se soit intéressé à de telles trivialités.
Le livre donne le résultat mais aucune solution.
Pour le moment je dispose de deux méthodes dont l'une devrait beaucoup plaire à Imod que je salue.
Amicalement
pappus
Bonjour
Tout dépend de ce que l'on cherche exactement . On peut construire la figure facilement , les centres des cinq cercles sont les sommets et le centre d'un carré . On obtient des tangentes aux cercles en traçant les droites passant par les milieux de deux côtés consécutifs de ce carré , ...
Imod
Mon cher Malou
....
Amicalement
pappus
Autant le savoir du départ...malou est du genre féminin


Bonne journée à toi
Cher Pappus
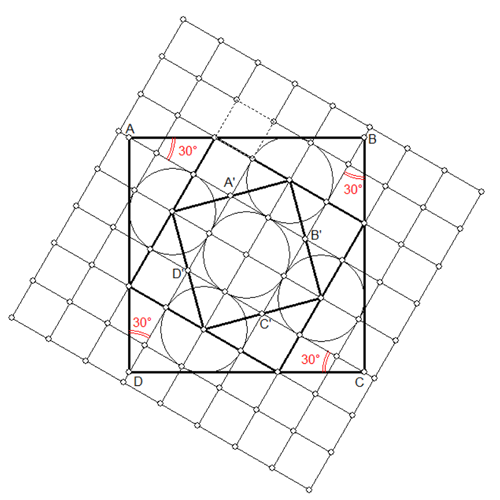
Je pense avoir trouvé la méthode qui devrait me plaire et qui me plait à l'aide d'un simple quadrillage 4X4 . Je laisse chercher les autres 
Imod
Ma chère Malou
Excuse le nouveau que je suis mais avoue que nos discussions sont un peu désincarnées.
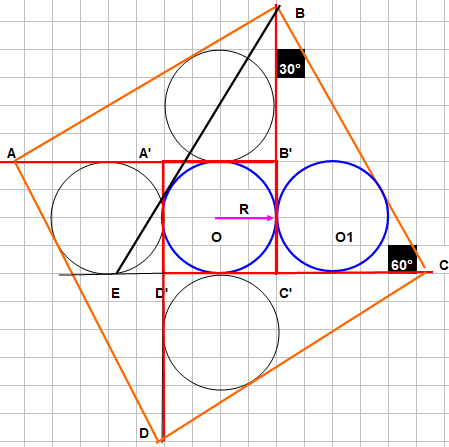
Voici une de mes constructions qui devrait satisfaire Imod.
Amicalement
pappus
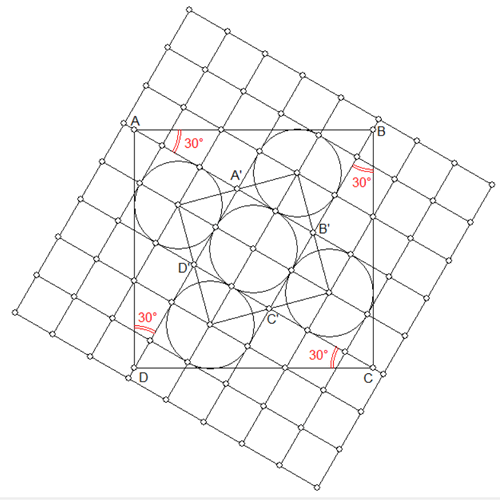
J'étais en train d'illustrer mais je suis un peu long , voilà mon image ( je n'ai pas regardé les angles ) :
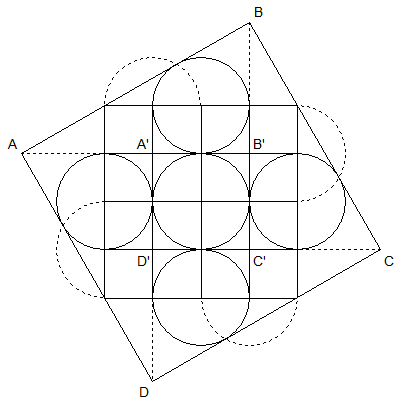
Imod
Bonjour à tous,
Je découvre et je cherche du côté des similitudes (une directe, une indirecte de même rapport)
Je pense pouvoir aboutir mais il me faut un peu de temps ...
Je reste un peu dubitatif sur les angles 30° et 60° construits sur un quadrillage , tout dépend de ce qui est autorisé ou interdit .
Imod
Bonjour à tous
Bien sûr les points ne font pas partie du quadrillage, l'essentiel étant de montrer que
Amicalement
pappus
D'accord pour les angles . Je ne les avais pas indiqués sur mon dessin car je ne les avais pas utilisés mais ils étaient bien là .
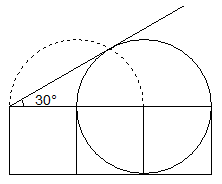
Imod
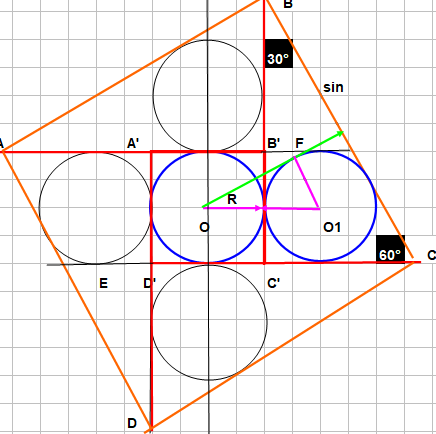
c'est ce que je cherchais avec mon rayon rose
Dans le triangle O O1 F
On a sin(0)= R/2R = 0.5-->asin (O.5) =0.523598...=30° et avec les
triangles semblables on a bon