Inscription / Connexion Nouveau Sujet
Rayon d'une capsule
Bonjour,
Petit exo qui me fait galérer :
Je cherche à connaître le rayon (R) d'une capsule sachant que je connais sa hauteur (H) et son volume V.
Les terminaisons sont sphériques (demi sphères parfaites). En attache, un dessin pour illustrer (à imaginer en 3D bien entendu).
Merci beaucoup !!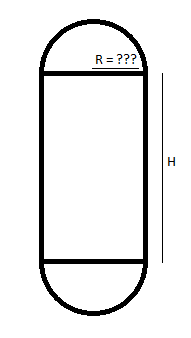
***forum modifié***
Bienvenue, mais.....
quel est ton profil ? pour savoir le niveau auquel on peut t'aider , et aussi pour le changer de forum....
c'est du niveau 3e à peu près
Bonsoir,
il suffit de résoudre l'équation du troisième degré
Mais la résolution exacte n'est pas du niveau troisième.
impossible de donner H et V, ce sont des variables. le but c'est d'avoir l'algo qui me donnera la réponse.
Je me doutais bien que ça serait effectivement un équation du 3ème degré mais je n'ai pas été jusque là dans mes cours de maths en mon "jeune" temps.
et mon profile, c'est ingénieur en informatique. Je bute sur ce problème alors que je dois l'intégrer à un logiciel que je développe 
bon, la demande est plus claire...j'ai modifié le forum...vous pouvez choisir "reprise d'études " dans votre profil (cela indique que vous essayez de résoudre qq chose avec pas nécessairement toutes les connaissances requises, merci )
malou (modérateur)
Bonjour,
comme il s'agit d'une équation du troisième degré, une "formule" donnant R en fonction explicite de H et V est illusoire
(formules de Cardan etc)
pour inclure ça dans un programme, le mieux est de faire un calcul d'approximations numériques (dichotomie ou mieux méthode de Newton)
comme R est plus petit que s'il ne s'agissait que d'un simple cylindre, une valeur de départ pour ces algorithmes est calculable facilement (en résolvant )
la méthode de Newton converge très rapidement vers une solution approchée
le principe de tels algorithmes est trouvable facilement sur le net.
Merci à tous pour votre retour et pour le déplacement du post
Il ne me reste plus qu'à investiguer pour trouver cet algo de la méthode de Newton.
Ca me scie un peu qu'il ne soit pas possible de résoudre cette équation quand on sait qu'il n'y a qu'une réponse possible.
J'ai aussi trouvé cette méthode : ![]()
Est-ce qu'à votre avis elle ne me permettrait pas d'arriver à un résultat?
si h et v sont les paramètres une simple dichotomie avec le couple (0, v) suffit amplement il me semble ...
je ne pense pas que la différence de temps soit perceptible à l'humain entre la dichotomie et Newton ...
puisque 2^3 = 8 et 2^4 = 16 on gagne une décimale à chaque fois qu'on passe de n à n + 4 en gros ...
Bonjour carpediem,
il y a quelque chose qui physiquement me choque dans ta valeur de départ vu que c'est un volume alors qu'on cherche (la variable) une longueur.
selon les unités choisies on pourra donc très bien avoir f(v) et f(0) pas de signe contraire ce qui met en échec la dichotomie.
(la solution est en dehors de [0; V])
il vaut mieux partir comme je le préconisais de ou un majorant grossier de cette valeur avec π = 1 par exemple.
(qui est bien une longueur, et dont on sait que le R solution est forcément inférieur à cette valeur)
Pour la méthode de Newton ça n'a aucune espèce d'importance, on peut partir de absolument n'importe quelle valeur > 0 vu les variations de la fonction pour x > 0.
on peut tout aussi bien partir de R = 1 !
chaque méthode a ses avantages et ses inconvénients...
en 0 on obtient -v donc f(0) < 0 ...
effectivement on ne sait pas quels sont les ordres de grandeur de h et v
et f(v)  4v^3 + 3hv^2 - v peut effectivement être négatif aussi si v et h sont "petits" ....
4v^3 + 3hv^2 - v peut effectivement être négatif aussi si v et h sont "petits" ....
Bonjour à tous.
Pour info, je me suis basé sur cet algorithme de résolution d'équation du 3ème degré : http://codes-sources.commentcamarche.net/source/view/9731/749025#browser
Il fonctionne parfaitement et me renvoie, pour l'équation \frac43\pi R^3+\pi H R^2-V=0 toujours une et une seule solution.
Étant donné que mes entrées sont toujours correctes (j'ai toujours un volume et une hauteur cohérente), j'ai des résultats parfaits.
Du coup, grâce à cela, je peux simuler des taux remplissage de réservoirs de carburant sur des satellites 
Merci à tous pour votre implication dans mon projet.
Autant pour moi, j'ai trouvé des cas à plusieurs solutions, mais j'ai toujours une seule solution positive, donc c'est celle que je cherche.
oui, c'est la seule solution positive qui compte quand il y en a plusieurs.
(il est d'ailleurs inutile de calculer les autres !)
nota : cet algorithme est le même que celui proposé par Lafol en Javascript le 07-07-16 à 16:23
comprendre comment il fonctionne est plus compliqué (formules de Cardan etc niveau math sup en maths) que comprendre un algorithme par dichotomie (niveau première/terminale en programmation),
algorithme qui permettrait de résoudre n'importe quelle équation, pas seulement du 3ème degré. et qu'il est donc extrêmement utile de connaitre (bien plus que la méthode de Cardan pour les équations du 3ème degré)



