Inscription / Connexion Nouveau Sujet
Recherche d'un élément dans une liste
Bonjour à tous
J'ai un problème dans un exercice de programmation, et j'aimerais votre aide parce que je suis vraiment bloqué
On considère deux listes d'entiers tous différents L1 et L2 qui sont triées, et on me demande de trouver le kième plus petit élément de la réunion de ces deux listes, avec une complexité O(log (n)) , où n est le maximum des tailles de liste L1 et L2
Je suis parti sur l'idée d'une dichotomie, mais je n'arrive pas à aboutir...
Si quelqu'un peut me mettre sur la voie, je lui en serais reconnaissant =)
Merci d'avance !
Les entiers sont différents dans une même liste.
Le sont-ils aussi entre L1 et L2 ?
Autrement dit l'intersection entre L1 et L2 est vide, c'est ça ?
Salut.
Alors j'ai un petit souci : qd j'ai lu l'énoncé, j'ai tout de suite pensé à un algo, seulement il n'est pas en log(n)...
Alors voilà mon raisonnement :
- soient i1=0 et i2=0 deux indices de parcours des listes, et 'liste' l'indice de la liste dans laquelle est la dernière valeur triée
- tant que i1+i2<k :
- si L1[i1]<L2[i2] (*)
-si i1<taille(L1)
i1++
liste=1
- sinon
i2++
liste=2
- sinon
-si i2<taille(L2)
i2++
liste=2
- sinon
i1++
liste=1
A la fin de l'algo, si liste vaut 1, alors l'élément recherché est L1[i1-1], sinon L2[i2-1].
Pour le (*), il doit y avoir une subtilité : il ne faut pas que l'indice dépasse la taille du tableau...
J'ai pondu un petit code Python pour valider tout ça :
- je commence par créer UNE liste l, dont je récupère la k-ième valeur pour validation de mon raisonnement
- je "splite" cette liste entre deux listes L1 et L2, puis j'applique l'algo ci-dessus
- je compare la valeur de sortie de l'algo à la valeur de référence : c'est la même !
Voilà le code ci-dessous :
import random
log = False
maxVal = 100
n = 15
for i in range(100):
if log:
print('-'*60)
# Création de la réunion des deux listes
l = []
while len(l)!=n:
val = int(random.random()*maxVal)
if not val in l:
l.append(val)
l.sort()
if log:
print('L =',l)
# Création des deux listes
l1 = []
l2 = []
for i in range(n):
if random.random()<0.5:
l1.append(l[i])
else:
l2.append(l[i])
if log:
print('L1 =',l1)
print('L2 =',l2)
# Calcul du k-ème plus petit élément de l'intersection
k = int(random.random()*(n-2)+1)
if log:
print('Recherche de la ',k,'-ième valeur')
i1 = 0
i2 = 0
liste = 0
while i1+i2!=k:
if l1[min(i1,len(l1)-1)]<l2[min(i2,len(l2)-1)]:
if i1<len(l1):
i1+=1
liste = 1
else:
i2+=1
liste = 2
if log:
print(i1, i2, liste, l1[i1-1])
else:
if i2<len(l2):
i2+=1
liste = 2
else:
i1+=1
liste = 1
if log:
print(i1, i2, liste, l2[i2-1])
if liste==1:
found = l1[i1-1]
else:
found = l2[i2-1]
if log:
print(k,'-ème valeur trouvée :',found)
print('Valeur attendue =',l[k-1])
print(found-l[k-1])
Comme je le marquais plus haut, ce qui me gène c'est que cet algo n'est pas en O(log(n)), mais en O(k) (du moins il me semble, je n'ai jamais été fichu d'évaluer correctement la complexité de mes algo...).
Voilà, j'espère avoir apporté un peu d'eau à ton moulin !
Bonsoir Simpom
Effectivement j'ai déjà pondu un algo de cette sorte, et effectivement il est en O(k). Sinon on peut aussi fusionner les deux listes l1 et l2, mais là c'est en O(n1 + n2) où ni = len(li), ou encore essayer de créer les deux listes de taille n/2 pour faire une dichotomie, mais là c'est en O( n log n) avec mon programme
Du coup la véritable difficulté c'est de trouver un algo en log(n) ... Mais merci pour ta réponse, si jamais tu as une nouvelle idée je suis preneur =)
La je pense que je vais laisser passer cette nuit : on dit souvent qu'elle porte conseil 
Encore merci et bonne nuit !
Un coup de divide and conquer (diviser pour gagner).
Supposons pour simplifier que est une puissance de
, disons
, et que
est inférieur ou égal au minimum des longueur des deux listes triées que je vais appeler
et
.
On sait au début que le -ème plus petit élément, appelons-le
, se situe dans
ou dans
.
Supposons que . Alors
se situe dans
ou dans
. Si au contraire
, alors ...
Je te laisse continuer.
Bonjour.
Une idée d'informaticien (nul n'est parfait)...
A partir des listes L1 et L2, on génère les listes Lbis1 et Lbis2 telles que :
Lbis1[ni] = 1 si l'entier ni est présent dans la liste L1
Lbis1[ni] = 0 si l'entier ni est absent de la liste L1
Lbis2[ni] = 1 si l'entier ni est présent dans la liste L2
Lbis2[ni] = 0 si l'entier ni est absent de la liste L2
Il suffit ensuite de balayer les deux listes indexées Lbis1 et Lbis2 en parallèle avec les tests adéquats.
A+
GaBuZoMeu, bonjour.
En 35 ans de développement en informatique embarquée (je sais, je fais partie de la préhistoire de l'informatique juste après le boulier, la règle à calculs et les tables de log), je n'ai jamais entendu parler de complexité d'un algorithme dans le cadre de mes nombreuses expériences professionnelles...
Au vu de la puissance de calcul des processeurs actuels, est-il valable de perdre du temps à gagner quelques opérations ?
Par contre, taille du processeur (de 1 bit à 128 bits), taille de ses mémoires mortes ou vives, fréquences d'horloge, code sans 'bogues' et surtout le coût d'un processeur et de son environnement (et j'en oublie), ça oui...
Cordialement.
Alors pourquoi interviens-tu sur une question concernant la complexité d'un algorithme ?
Puisqu'ici c'est bien le noeud de l'affaire !
Au vu de la puissance de calcul des processeurs actuels, est-il valable de perdre du temps à gagner quelques opérations ?
Tu devrais pouvoir comprendre qu'il y a une sacrée différence entre un algorithme avec complexité en
bonjour,
je me permet d'ajouter que si on utilise la notation grand O en complexité, c'est pas par paresse, c'est parce que justement on prend en compte l'accélération matérielle. Qu'un processus s'execute en temps ou
, c'est équivalent à un changement de matériel près.
Par contre, entre un algo linéaire et un algo logarithmique, il existera toujours une différence dans le temps d'exécution.
Par contre, entre un algo linéaire et un algo logarithmique, il existera toujours une différence dans le temps d'exécution.
... pour toute entrée suffisamment grande.
Bon, ravinator semble se désintéresser de son fil...
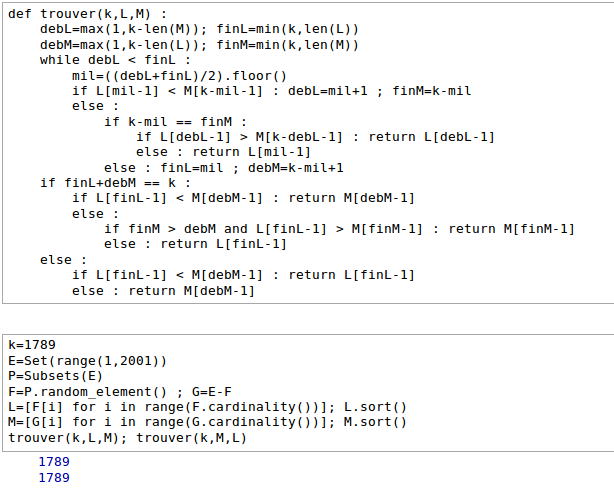
Pour conclure tout de même, voici un petit programme écrit en Sage qui fait le travail (trouver le k-ème à partir de deux listes disjointes L et M triées dans l'ordre croissant). Il n'est pas inutile de savoir que Sage indexe les listes à partir de 0. Le programme fait boucles avec un test dans chaque boucle : on a bien une complexité en
, donc en
puisque
.
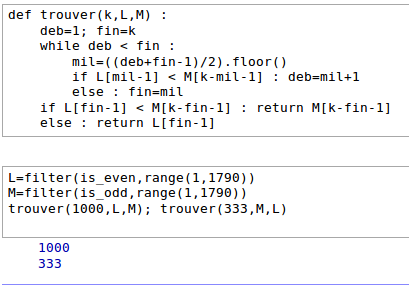
Je n'ai jamais utilisé Sage, mais comme ça je dirais qu'il va y avoir un souci si une des liste a une taille inférieure à k/2. Dans tous les cas j'aime bien l'idée de recycler les bugs en exercices 
(et je suis d'accord avec la précision de Bachstelze, j'ai été un peu rapide dans ma formulation)