Inscription / Connexion Nouveau Sujet
Rectangles semblables
Bonjour à tous 
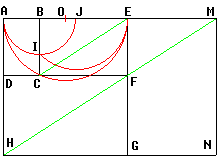
J'ai découpé un rectangle en trois rectangles différents et pourtant semblables au rectangle initial :
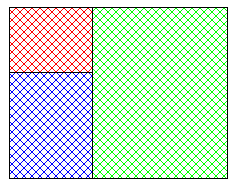
On peut chercher le rapport entre les côtés de ce rectangle mais surtout se demander si le même découpage est possible en quatre , cinq , six , … morceaux .
Amusez-vous bien 
Imod
Salut Imod.
On peut faire un découpage en quatre sans vraiment se fatiguer. Il suffit de tracer les médiatrices des côtés.
On a alors tous les nombres de la forme 4+3n.
Autre méthode
 Cliquez pour afficher
Cliquez pour afficherBonjour,
différents est il dit
(tous les rectangles doivent être différents les uns des autres)
 Cliquez pour afficher
Cliquez pour afficherSans se lancer dans des considérations compliquées , tu remarqueras qu'en partant d'un partage en 3 avec les deux découpages déjà donnés , on peut faire énormément de choses .
Imod
mais il n'est pas possible de "combiner" deux découpages en n et en n' car les rectangles n'ont pas la même forme (Longueur / largeur)
(si on découpe en 3 un des 4 rectangles de la découpe en 4, ça ne marche pas...)
Ok , tu as raison , je me suis emballé .
Il y a tout de même un découpage "universel" du style de celui que j'ai donné en introduction . Après il faut justifier qu'on peut choisir le rapport des côtés de façon à ce que le grand rectangle soit dans les bonnes proportions .
Imod
à mon sens il y a deux cas à considérer, n pair (à partir de la découpe en 4) et n impair (à partir de la découpe en 3)
 Cliquez pour afficher
Cliquez pour afficherOui , il reste à justifier pourquoi on peut aligner les points A , C et U . Il y a certainement une continuité qui traîne .
Imod
Une autre approche . On empile les rectangles sur la longueur du bloc déjà construit , celle-ci devenant sa largeur . On finit avec un rectangle dont la longueur est cette fois-ci la longueur du bloc .
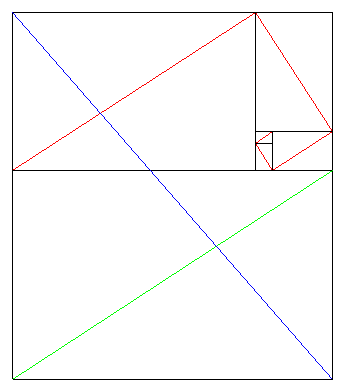
On obtient alors une spirale orthogonale . "On voit" facilement en manipulant les dimensions du rectangle initial que l'on peut donner la même forme au grand rectangle ( segments verts et bleus perpendiculaires ) .
Il reste à donner du sens au "On voit" .
Imod
Bonjour Derny , je ne vois pas de quoi tu parles , la forme du rectangle dépend clairement du nombre et de la disposition des morceaux . Dans les figures déjà proposées le rapport est racine d'un polynôme dont le degré augmente avec le nombre de morceaux . On a par exemple sur les dessins précédents des rapports qui valent :
Imod
pour mes rectangles "avec gnomons" le rapport L/l est différent et il faut le recalculer chaque fois qu'on ajoute deux rectangles
c'est pareil avec la méthode de Imod 23-03-23 à 12:39.
et le rapport est racine d'un polynôme dont le degré augmente avec le nombre de morceaux .
(et la flemme de calculer une formule d'itération sur ces polynomes)
nota : euh ... c'est pour la découpe en 3 que le ratio est
en 4 c'est
Je crois que j'ai réussi à finaliser le truc , la construction de Mathafou se laisse mieux appréhender que la mienne . On a un gros rectangle de côtés a et b auquel on ajoute deux rectangles formant un "L" . Le rapport longueur/largeur de chacun des morceaux est noté k :
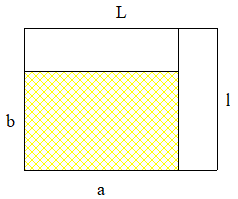
Le rapport est égal à
. Bien sûr a et b dépendent de k mais ce n'est pas grave . Quand k tend vers 1 le rapport est supérieur à 1 et quand k tend vers l'infini il tend vers 0 , il passera donc par 1 et c'est fini .
Imod
Bonjour
Effectivement j'ai écrit n'importe quoi. Pour avoir un rapport de V2 il faut "au départ" 2 rectangles identiques (voir ci-dessous).
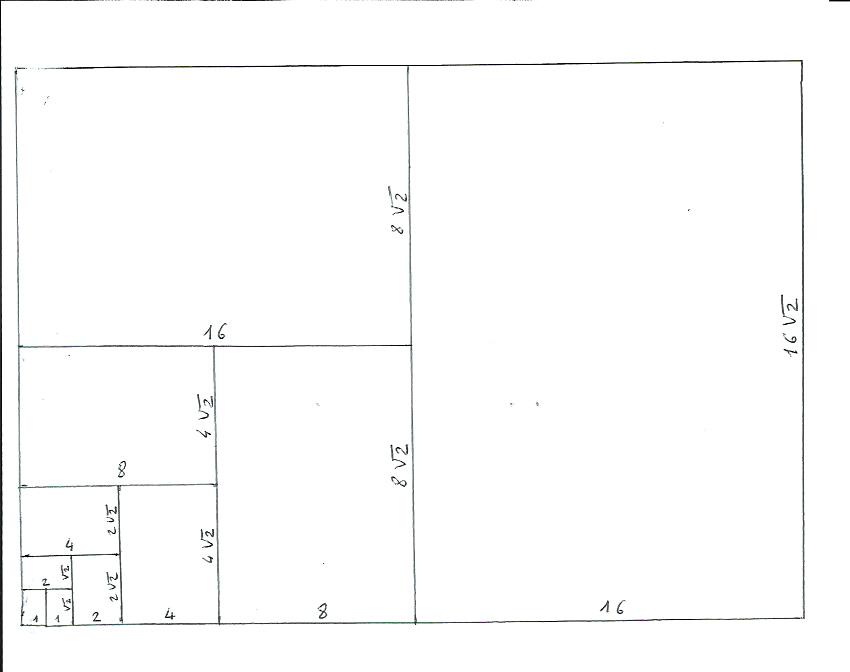
Je me demandais si on était obligé de distinguer les cas pairs et impairs car le "L" peut envelopper un nombre pair ou impair de rectangles mais il y a le problème de l'amorce quand le rectangle de côtés a et b est le plus petit rectangle . On ne peut donc pas échapper au cas de la coupe en trois avec un rapport .
Imod
Bon soir
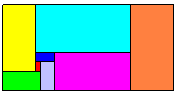
J'aime bien les rectangles de mathafou. du 22 à 17h30. Les colorés sont, comme dit, d'un rapport 1/2. Ce qui fait 9 rectangles semblables en comptant le rectangle extérieur.
Pour les rectangles au-dessus les calculs sont faciles. Le rapport est de 1/V(1+V2.5) soit environ 1/1.606592304... Ce qui fait 7 rectangles semblables en comptant le rectangle extérieur. Le petit bémol est qu'ici, tous les rectangles intérieurs possibles ne sont pas dans ces proportions (quand on peur regrouper certains rectangles intérieurs).
Comment as-tu trouvé ces découpages ? Par tâtonnements ?
La construction de Mathafou est plutôt naturelle en observant les angles droits entre les diagonales de deux rectangles successifs d'orientations différentes . C'est un peu la même idée que la mienne .
Imod
Imod, pour continuer ta spirale rouge (le 23 à 12h39)avec des angles droits, ton dernier rectangle n'est pas bon. il faut poursuivre par une longueur au lieu d'une largeur. Si c'est pour avoir le rectangle extérieur dans les mêmes proportions que les rectangles intérieurs ce n'est pas bon non plus.
il va falloir répéter encore et encore que en ajoutant des rectangles à l'extérieur, il faut obligatoirement changer le rapport ...
c'est dit dès le départ :
en manipulant les dimensions du rectangle initial ...
et c'est dit aussi que le dernier n'est pas "la suite de la spirale" mais dans l'autre sens
(évident que si on le poursuivait en spirale ça ne peut pas marcher)
avec cette disposition et ce nombre de rectangles il est nécessaire de calculer jusqu'au bout pour obtenir une équation dont la solution donne le rapport cherché pour cette disposition, seule valeur qui assure l'angle droit voulu.
poursuivre un tour de plus (ou un tour de moins) nécessite un autre rapport à recalculer
le détail :
le rapport est ici la solution positive de
qui est  1.30739...
1.30739...
au départ "en manipulant" veut dire en ajustant à la main pour avoir l'angle droit
ici je l'ai fait par le calcul.
ce que confirme Geogebra en affichant bien un angle droit.
et pour ma découpe du 22-03-23 à 17:30, en 6 aussi, mais disposition différente, le détail des calculs :
en bleu une construction synthétique de
disposition différente, équation différent et donc valeur différente de la disposition de lmod du 23-03-23 à 12:39, détaillée dans mon dernier message.
(qui elle n'est pas constructible à la règle et au compas : équation degré 3 en l'inconnue x²)
Je pense avoir trouvé une approche plus uniforme du problème :
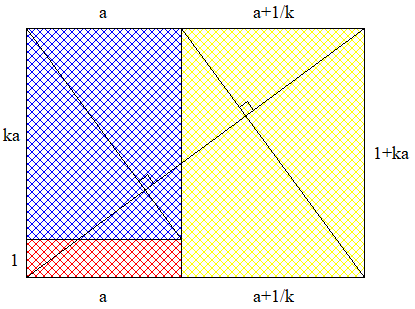
En partant d'un rectangle aX1 construit à partir de rectangle de rapport longueur/largeur=k , on peut toujours choisir k pour que le rapport longueur/largeur du grand rectangle soit aussi k . J'ai longtemps été empoisonné par les possibles inversions longueur<->largeur , quand on fait varier k .
Imod
la difficulté est ici de bien voir que a dépend de k ...
on aboutit à l'équation
a(k)k^3 +k^2 +2a(k)k -1 = 0
dont il ne semble pas franchement simple de dire quoi que ce soit sans connaitre a(k) ...
C'est bien la difficulté , j'avais déjà esquissé le problème lors d'un message précédent . Il me semble qu'il faut voir si le résultat du message précédent est juste . Après en mettant ce qu'il faut dans le rectangle rouge on conclut facilement .
Imod
Ta dernière méthode, si on part du rectangle 1:k lui même, donne ce que l'on savait déja :
on peut découper en un nombre impair quelconque avec toujours le même rapport de
(c'est en fait vu autrement la découpe en 3 dont on subdivise récursivement le plus petit rectangle en 3)
avec ce rapport là, à chaque paire de rectangle que l'on ajoute , les points A, C, H, L, P etc sont alignés
Deux jours sans informatique est idéal pour se remettre les idées en place 
On cherche un rectangle que l'on peut découper en n+1 ( n>1 ) rectangles tous distincts et semblables au rectangle initial . On effectue notre montage de la façon suivante :
On part d'un rectangle 1 X k avec k>1 . La longueur de ce premier rectangle va devenir la largeur du deuxième . La largeur du troisième sera la longueur du bloc formé par les deux premiers et ainsi de suite jusqu'au nième rectangle . La longueur du dernier bloc servira de longueur au dernier rectangle .
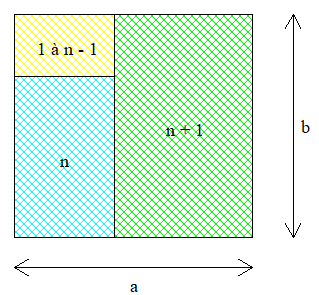
Les premières largeurs se calculent aisément et on obtient les longueurs en multipliant par
. On note que ces largeurs sont de type
avec
qui tend vers 0 quand k grandit . Le dernier rectangle ne suit pas la même logique :
et
. On obtient
et
.
Considérons .
Quand k tend vers 1 , b et a s'approchent de deux termes successifs de la suite de Fibonacci donc R est supérieur à 1 . A l'opposé quand k tend vers l'infini R tend vers 1/2 . Comme R varie continûment en fonction de k , il prendra la valeur 1 et c'est fini .
Imod
Oui, 
ceci est en fait ta construction en spirale du 23-03-23 à 12:39
et complète le "on voit" par une preuve rigoureuse.
on peut en rester là puisque on cherche un découpage en n
Sans aller jusqu'à calculer les différentes dimensions des rectangles , il fallait tout de même regarder les différents polynômes qui ont le bonheur d'être unitaires avec un degré incrémenté de 1 à chaque étape . C'est comme souvent évident après coup .
Merci pour ta participation toujours très efficace 
Imod
Bonjour
J'ai étudié tous les cas jusqu'à 9 rectangles intérieurs en ajoutant chaque fois un rectangle contre la longueur(longueur qui devient longueur du rectangle rajouté) et le rapport des côtés par cette méthode se rapproche de V2 par valeurs alternées. Ci-dessous le cas de 8 triangles intérieurs. Pour n=9 on a 1.41115...
ce n'est pas la méthode de lmod mais une autre
dans la méthode de lmod le 3ème rectangle a pour largeur 1+a² et pour longueur a+a3 etc
cette méthode (de lmod) à comme il le dit l'avantage de simplifier les calculs car la règle de passage au cran suivant est très simple. (que des polynomes unitaires, c'est à dire dont le coefficient de plus haut degré est 1)
alors que la tienne fait intervenir des fractions. (des polynomes généralisés à des exposants négatifs)
comme déja dit il n'y a pas que un seul découpage possible pour un n donné
- découpage en spirale de lmod
- ajout de gnomons (une forme en L formée de deux rectangles, de même orientation) de lmod
- ajout de gnomons (deux rectangles d'orientation différente) de mathafou
- redécoupage récursif à partir d'un découpage en p tel que n = p+k(p-1)
et certainement "etc" (mix de plusieurs de ces méthodes)
Oui l'idée derrière cette construction était de régler le cas "pair" , on pourrait tout aussi bien démarrer les gnomons sur un autre rectangle obtenu avec un aggloméra de rectangle semblables . Après on peut s'intéresser dans ce cas particulier à la limite du rapport L/l pour lequel le grand rectangle est semblable à celui du rectangle initial mais c'est plutôt artificiel .
Imod
la construction en spirale a l'énorme avantage de mettre dans le même sac les cas pairs et impairs
alors que l'ajout de gnomons formés de paires de rectangles va de deux en deux, donc un point de départ différent pour le cas pair et pour le cas impair.
Avec la dernière méthode qui tend vers V2 on a tous les cas pairs et impairs semblables au rectangle initial et au rectangle extérieur bien sûr.
D'un autre côté le cas impair est tellement vite résolu qu'on a envie de trouver un moyen aussi simple pour résoudre le cas pair .
Je n'y crois pas trop 
Même s'il est du coup plus artificiel , le problème de Derny n'est pas inintéressant .
Imod

 A1+A1
A1+A1