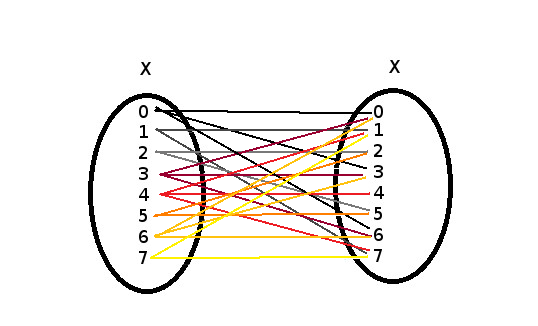
Mince ils me demandent le graphe et j'ai fait un diagramme de Venn bon de toute façon si mon diagramme et juste alors mon graphe le sera aussi ce qui m'intéresse c'est juste de savoir si les relations sont correctes

2) J'ai mal recopié désolé...

0R0, 0R3, 0R6
1R1, 1R4, 1R7
2R2, 2R5
3R0, 3R3, 3R6
4R1, 4R4, 4R7
5R2, 5R5
6R0, 6R3, 6R6
7R7 7R4, 7R1

3) On voit bien qu'il y a une relation d'équivalence car on remarque chaque fois que (par exemple) 7R4 <=> 4R7, 2R5 <=> 5R2 ... mais comment le montrer formellement ?

salut

C'est un R "barré" pour dire "pas en relation" justement.

Dans ce cas 2 éléments en relation on a : 1R4 et 2R5 par exemple

Autant pour moi je voulais faire un R barré obliquement, je reprends :

1) Deux éléments en relation : 1R4 et 2R5

Deux éléments qui ne sont pas en relation : 3Ꞧ2 et 6Ꞧ5

pourquoi abuser inutilement de symboles et ne pas le dire en français correctement ?

Désolé...

Dans ce cas :

x = 1 et y = 4 sont en relation par R, x = 2 et y = 5 sont en relation par R

x = 3 et y = 2 ne sont pas en relation par R, x = 6 et y = 5 ne sont pas en relation par R

Pour la question 2 :

On sait que :

0mod3=0
1mod3=1
2mod3=2
3mod3=0
4mod3=1
5mod3=2
6mod3=0
7mod3=1

Donc toutes les relations entre x et y par R sont :

0R0, 0R3, 0R6
1R1, 1R4, 1R7
2R2, 2R5
3R0, 3R3, 3R6
4R1, 4R4, 4R7
5R2, 5R5
6R0, 6R3, 6R6
7R1 7R4, 7R7

3) Je sais pas comment montrer que pour tout xRy il y a yR⁻¹x

que vient faire ce "puissance - 1" ?

ah oui non c'est la meme relation pardon mais comment le montrer autrement qu'en réécrivant chaque fois : xRy <=> yRx pour tous les x et y ?

x R y <=> x = y [3] <=> y = x [3] <=> y R x

...

Que signifie le "[3]" ?

[3] équivaut à "modulo 3"

ah merci je connaissais pas cette notation

signifie "a congru à b modulo 3"

merci Carpediem du coup... J'étais parti pour montrer la relation d'équivalence pour toutes les valeurs de x et y possibles

Pour la question 4 : j'ai du mal à comprendre la notion de "classe d'équivalence" même après avoir consulté Wikipédia.

Mais d'après ce que je pense avoir compris, il y a 3 classes d'équivalences non?

Je ne sais pas comment les définir... On les définit comme des ensembles ?

tout entier s'écrit 3k ou 3k + 1 ou 3k + 2 ...

D'accord Carpediem donc ça donne :

{∀x∈X ∃pℕ / x = 3p avec p ≤ 2}
{∀x∈X ∃pℕ / x = 3p+1 avec p ≤ 2}
{∀x∈X ∃pℕ / x = 3p+2 avec p ≤ 1}

mais normalement les classes d'équivalences sont censées réaliser une partition de X or les ensembles réalisant une partition sur un autre ensemble sont censés être disjoints et ici ce n'est pas le cas...

Si ils sont disjoints je me trompe une fois de plus ...

Pour la question 5 :

On appelle ensemble quotient de X par R l'ensemble des classes d'équivalence pour relation R.
On le note X/R.

à la question 4 on a vu qu'il y avait 3 classes d'équivalences :

{∀x∈X ∃pℕ / x = 3p avec p ≤ 2}
{∀x∈X ∃pℕ / x = 3p+1 avec p ≤ 2}
{∀x∈X ∃pℕ / x = 3p+2 avec p ≤ 1}

L'ensemble des classes d'équivalences c'est X j'vois pas ce que je dois faire au juste...

Je me trompe ?

X = {0, 1, 2, 3, 4, 5, 6, 7}

X/R = {0, 1, 2} = {1, 2, 3} = ... {5, 6, 7} = {0, 4, 5} = ...

Je comprends pas comment vous trouvez ces ensembles ?

il n'y a qu'un seul ensembles X/R

cl (0) = {0, 3, 6}
cl (1) = {1, 4, 7}
cl (2) = {2, 5}

X = cl (0) U cl (1) U cl (2)

et cl (0) = cl (3) = cl (6)

cl (0) est l'ensemble des éléments de X en relation avec 0 par la relation R

donc X/R = {cl (0), cl (1), cl (2)}

Bonjour
tu n'as absolument pas compris la question 3....
on ne te demande pas de prouver que pour tous x et y, il y a équivalence entre x RY et y Rx, mais on te demande de prouver que R est une relation d'équivalence...
ça contient ce qui précède (qu'on traduit en disant que R est symétrique) mais il te reste à justifier que R est réflexive, et aussi que R est transitive...

relation d'équivalence et équivalence logique (au sens de double implication) ce n'est pas du tout la même chose !

Merci bcp pour toute l'aide que vous m'avez apporté

de rien