Niveau Master Maths

Relation d'équivalence théorème de factorisation généralisé

Posté par
Barjovrille 28-09-23 à 18:36

Bonjour,
Soit $X,Y$ , deux ensemble et $R_X , R_Y$ deux relations d'équivalence (une sur X et l'autre sur Y).
Il est bien connu que si une fonction $f : X \to Y$ vérifie :
pour tout $x,x' \in X$ tel que $x R_X x'$ , alors $f(x) =f(x')$ . Alors on peut passer au quotient, ie : il existe application $f_* : X/R_X \to Y$ qui vérifie $\pi_X \circ f_* =f$ . Où $\pi_X$ est la surjection canonique. L'application $f_*$ est unique il n'y a pas d'ambiguité. (Exemple le plus connu je pense le cas où $f : X \to Y$ est un morphisme de groupe et on quotiente par le noyau pour avoir une fonction $f_* : X/ker(f) \to Y$ )

Est-ce-que si la fonction $f$ vérifie : pour tout $x,x' \in X$ tel que $x R_X x'$ , alors $f(x) R_Y f(x')$ . Alors je peux parler sans ambiguïté d'une fonction $f_* : X/R_X \to Y/R_Y$ . J'ai l'impression qu'il n'y a plus unicité ?

Si quelqu'un a des explications ou même des références.
Merci

Posté par re : Relation d'équivalence théorème de factorisation généralisé 28-09-23 à 18:40

La question est peut être un peu vague, peut être cette formulation est meilleure (ou pas) :
Avec les même notations est ce que la fonction $* : A((X,R_X),(Y,R_Y)) \to A((X/R_X, Y/R_Y)), f \mapsto f_*$ est bien définie ?
Où $A(X,Y)$ est l'ensemble des applications de X dans Y.

Posté par re : Relation d'équivalence théorème de factorisation généralisé 28-09-23 à 18:48

Bonjour,
La réponse est facile : si on a une application $f : X\to Y$ , on peut la composer avec la surjection canonique $p: Y\to Y/R_Y$ . Et bien sûr $(p\circ f)(x)=(p\circ f)(x')$ si et seulement si $f(x)R_yf(x')$ . Maintenant il ne te reste plus qu'à appliquer le premier résultat de passage au quotient que tu cites à la fonction $p\circ f$ , dans le cas où pour tous $x,x'\in X$ , $xR_Xx'\implies f(x)R_Yf(x')$ .

Posté par re : Relation d'équivalence théorème de factorisation généralisé 28-09-23 à 19:54

Effectivement ce n'était pas si dur... Merci GBZM !

Posté par re : Relation d'équivalence théorème de factorisation généralisé 28-09-23 à 20:37

Bonsoir.
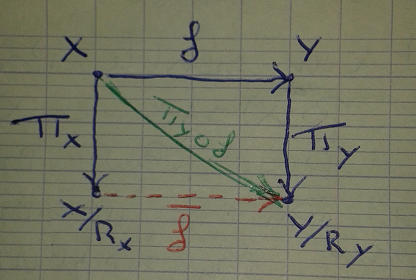
L'application $\pi_Y\circ{}f$ étant compatible avec la relation d'équivalence $R_X$ sur $X$ , l'existence et l'unicité de l'application $\overline{f}$ sont assurées par le premier résultat de passage au quotient que tu cites ; cette unique application est telle que

$\pi_Y\circ{}f=\overline{f}\circ\pi_X$

ce qui revient à dire que le diagramme ci-dessous (à la main) commute. L'explication de GBZM est cependant très claire et suffit largement à ton bonheur.

$Relation d\'équivalence théorème de factorisation généralisé$