Inscription / Connexion Nouveau Sujet
rencontre
Bonjour
je vous propose l'exercice suivant :
sur un parcours graduée de 0 à 10 ,deux mobiles A et B se trouvent sur les extremités de celui ci, A est initialement en 0 et b est initialement en 10. ces mobiles ne peuvent pas sortir des extremités de ce parcours , si A est en 0 il n'aura d'autre choix que de se deplacer en 1 , de même si B est en 10 il n'aura d'autre choix que de se déplacer en 9. les déplacements de ces mobiles de fait de façon aléatoire à droite ou a gauche et d'une unité à la fois et à chaque fois de façon simultanée.
On admet que A se deplace vers la droite avec une proba de 2/3 et Bque B se déplace vers la droite avec une proba de 3/7.
A l'instant t=0 les deux mobiles se lancent , en combien d'etapes en moyenne vont ils se retrouver sur la même graduation?
Bonsoir,
j'ai juste fait une simulation.
 Cliquez pour afficher
Cliquez pour afficherLe calcul exact me semble difficile, mais j'ai peut-être raté une astuce.
Si ça intéresse quelqu'un voici le code python utilisé.
 Cliquez pour afficher
Cliquez pour afficherSuite,
*La situation optimale est 11 (tous les déplacements favorables)
*une importante zone de contacts est comprise entre 12 et 16
* on peut imaginer un scénario défavorable** pour lequel malgré les proba 2/3 ;4/7 il n'y a jamais de contact
** dès les premiers coups
Bonsoir,
si tous les déplacements sont favorables A et B se retrouvent au point d'abscisse 5 en cinq mouvements chacun.
La probabilité de cet événement est
Voici la répartition des valeurs sur un million de parties :
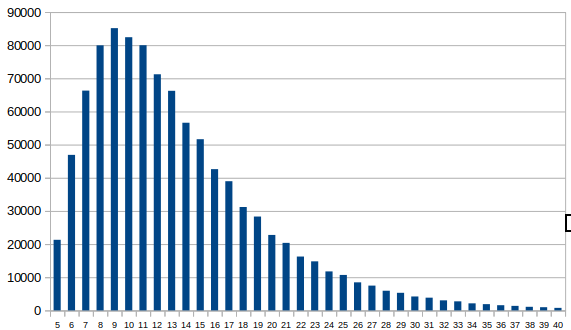
sur l'échelle verticale 10000 correspond à 1%.
J'ai supprimé les valeurs au delà de 40 ce qui fait 4182 parties soit 0,4%. La plus longue partie a 91 mouvements.





