Inscription / Connexion Nouveau Sujet
Représentation infinie d'une courbe .
Bonjour .
Voici un système de représentation d'une courbe qui permet d'avoir la totalité des point d'une courbe et de ses événements sous les yeux . Dans mes exemples , seul le quadrant ++ est représenté . On voit que les courbes classiques prennent des formes remarquables . Ceci n'est que le principe de base et ce système constitue une nouvelle manière de voir les mathématiques . En ce qui concerne la résolution j'avais réussi à obtenir la racine carrée de 2 en une seule opération !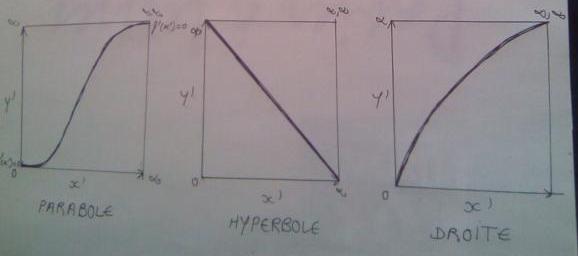
***image recadrée sur la figure***
Comme d'habitude, c'est laconique et imprécis. Pas vraiment faux car pas assez bien énoncé ou doté de sens pour qu'on puisse le réfuter. Et quand on fait un effort pour trouver ce que tu AURAIS PU vouloir dire, ça s'avère décevant, soit trivial soit bien connu, et toujours d'un niveau mathématique objectivement faible.
Bref, ça n'a rien d' "une nouvelle manière de voir les mathématiques".
Ces schémas, bien que visuellement sympathiques, ne veulent rien dire, faute d'explications suffisantes, explications qu'un élève de licence voire de terminale pourrait deviner mais, un il a autre chose à faire, et deux, une fois trouvé, ça ne va pas le nourrir intelectuellement plus de 2 secondes.
En ce qui concerne la résolution j'avais réussi à obtenir la racine carrée de 2 en une seule opération !
Moi aussi :
 2.
2.
J'ai faillit faire un pavé sur les gens dans ton genre, pour résumer : les personnes comme toi posent problème car vous êtes potentiellement dangereux pour le profane qui viendrait à vous lire, mais heureusement chacune de vos interventions est une bonne occasion de rappeler la nécéssité de bien raisonner et d'exercer son sens critique sans modération.
Ré .
Il est vrai que vous présenter les fondements de mon système est aussi abruti que vous decrire le plan euclidien : Ce ne sont que les bases . Vous ne voyez pas l'intérêt d'avoir TOUS les points d'une courbe sous les yeux ? C'est un bon moyen et qui représente une évolution par rapport au plan euclidien . Après vous pouvez jouer avec le point infini,infini en le positionnant à un endroit de la courbe : comme toutes les courbes atteignent ce point , toutes courbes tracées dans mon plan aura même Y pour un X donné , celui de l'infini . On peut donc calculer une racine carrée avec l'équation d'une droite !
Tout ce que vous faites c'est prendre une bijection  de [0,1[x[0,1[ sur R+² et tracer f o
de [0,1[x[0,1[ sur R+² et tracer f o  au lieu de f. Rien de nouveau et rien qui rende
au lieu de f. Rien de nouveau et rien qui rende  rationnel.
rationnel.
, Alain125 ce charabia, comme les précédents, n'a pas sa place sur notre site, ce serait bien de le comprendre...nous n'avons pas le forum adéquat....
(modérateur)
Ré .
Je n'ai pas réussi à me faire entendre ; vos avis sont mitigés . Mes travaux sont partiellement connus ce qui prête à confusion . Je n'ais pas eu d'autres interlocuteurs que vous en mathématiques , ce que je regrette . Il n'y a rien de prévu pour les gens comme moi .
salut
Ré .
Je n'ai pas réussi à me faire entendre ; vos avis sont mitigés . Mes travaux sont partiellement connus ce qui prête à confusion . Je n'ais pas eu d'autres interlocuteurs que vous en mathématiques , ce que je regrette . Il n'y a rien de prévu pour les gens comme moi .
ha mais tu les prêtes à qui tu veux ...

Nos avis ne sont pas mitigés, on est tous d'accord pour te dire que c'est n'importe quoi et tu ne veux pas l'entendre, "tes travaux" ou ce que tu t'appropries comme étant "tes travaux" sont déjà complètement connus dans une version intelligible, sans les bêtises dont tu agrémentes tes propos. Tu peux en parler à autant de matheux un minimum compétents que tu veux, ils te répondront la même chose. D'ailleurs les gens qui t'ont répondu sur ce forum ont des niveaux et des profils différents, ils ne se connaissent pas entre eux, il y a vraiment peu de chances qu'ils fassent partie d'une secte qui s'est jurée de persécuter toutes les personnes se prénommant alain. Il y a bien quelque chose de prévu pour les gens comme toi : leur expliquer que c'est n'importe quoi en sachant bien qu'ils ne l'entendront pas, mais ça aura au moins le mérite de prévenir le lecteur que c'est n'importe quoi et avec un peu de chance l'auteur de ce n'importe quoi se lassera.
Ré .
C'est bien dommage car pour parler des racines ce système est un outil formidable : j'ai fait ça il y a 20 ans de ça et comme les profs de maths n'ont pas donné de suites . Comme je vous dis , vous voyez que les courbes tendant vers + l'infini passent par ce point en X comme en Y . On pouvait jouer sur les coordonnées de ce point et faire passer la fonction racine carrée par le même point qu'une simple droite : le calcul se fesait en une seule fois contrairement aux méthodes classiques qui demandent de répéter la calcul et ne fournissent qu un résultat approximatif .
On pouvait jouer sur les coordonnées de ce point et faire passer la fonction racine carrée par le même point qu'une simple droite : le calcul se fesait en une seule fois contrairement aux méthodes classiques qui demandent de répéter la calcul et ne fournissent qu un résultat approximatif .
Ok, j'attends.
Ré .
Donc voilà , mais ça fait plus de vingt ans que j'ai fait ça et je me souviens à peine des détails . Je voulais surtout insister sur le fait que cette représentation infinie permet d'avoir la totalité des points d'une courbe et de ses événements sous les yeux .
Bonsoir,
moi je m'attendais plutôt à une réponse "à la Fermat" ("la marge est trop petite ..") arguant de développements trop longs pour être exposés ici (mais la comparaison avec Fermat s'arrête là, faut pas pousser  )
)
ou bien un bottage en touche par une digression sans aucun rapport
mais le coup du "j'ai oublié comment j'avais fait" c'est la première fois qu'il nous la sort.
Ré .
C'est malheureusement la vérité . Mais ce n'est pas si compliqué que ça et peut facilement se déduire de ce qu je vous ai déjà dit . Mais il est vrai qu'à l'époque j'étais arrivé à ce résultat , ce qui donc n'est pas impossible .
Et si on arrêtait d'essayer de le convaincre qu'il a tort puisque jamais il ne l'admettra.
Sans réponse, il finira peut être par se lasser de prêcher dans le désert.
Allez on s'octroie juste un message réponse pour prévenir les éventuels lecteurs que c'est du n'importe quoi.
et franchement ça sert à quoi de dire ça sur ce site ? y a 20 ans, j'ai fait quelque chose mais je ne m'en souviens pas ....
nous sommes un site d'aide pour collégiens, lycéens et personnes du supérieur qui étudient les maths ; en aucun cas nous ne voulons héberger le type de messages que tu nous envoies depuis quelques temps. Cherche un site qui te correspond, mais ce n'est pas ici.
(modérateur)
il a dit à quoi servaient ses messages ici : exclusivement à augmenter son page rank sur Google, le contenu n'a aucune importance et peut être une bulle de savon pleine de vide.
remarquer toutefois que la section "expresso" n'est pas consacrée à une aide
mais des sujets quelconques (en rapport avec les maths) : "Forum libre de discussion pour tous les habitués du site..."
mais de là à y mettre des délires, ou annoncer un "résultat" qu'on refuse en fait de donner pour diverses raisons foireuses...
Bonjour .
Je pense qu'à cause de mon personnage vous refusez de reconnaître un intérêt dans mon travail . Quand-même ... Un nouveau système de représentation des courbes qui marche de - l'infini à +l'infini , c'est quand même nouveau et cela mérite votre intérêt .
Quant à moi , il faut vous dire que j'ai été publié 3 fois par les professeurs de mathématiques au niveau national pour des mathématiques dont la complexité, là , mérite bien le second message de Schtompfmol .
Ré .
J'aimerais bien vous faire voir mes publications , mais on a pas le droit dans ce forum de scanner du texte .
@Mathafou .
J'ai survolé le texte que tu m'as soumis . Cela prouve bien l'existence d'autres plans que le plan euclidien et qui fait intervenir les hyperboles , comme dans mon plan .
Cela prouve bien ...
 2 entre autres), ce qu'il y a de novateur dans tes écrits.
2 entre autres), ce qu'il y a de novateur dans tes écrits.
que envoyer les points à l'infini sur des points finis d'un dessin est loin d'être une idée neuve.
mes publications ...

si c'est publié c'est disponible quelque part (comme le document dont j'ai donné le lien) ou avec un numéro de publication ISBN ou une référence dans une archive.
sinon eh bien c'est que ce n'est pas publié...
et puis du texte, à moins que ce ne soit que des gribouillis écrits à la main sur papier, cela se copie en quelques clics de nos jours.
en fait sans définitions précises, tout ce que tu annonces est du blablabla.
mais quand on te demande des précisions tu es incapable de les donner car elles n'existent pas.
Si mon idée était connue , je le saurais . Ce que je vous ai dit sur la racine de de 2 peut se retrouver d'après les éléments que je vous ai donné , moi je ne m'en souviens plus très bien et j'ai décroché des maths il y a 20 ans de ça .
C'est dans le bulletin de l'APMEP ( Association des Professeurs de Mathématiques de l'Enseignement Public ) que j'ai été publié . Octobre 1993 numéro 390 page 500 ; avril-mai 1996 numéro 403 page 203 ( le collègue c'est moi ) et décembre 1996 numéro 407 page 744 dans lequel ils parlent de moi .
Voilà . Peut être les retrouverez-vous ?
Ré .
Non mais vous imaginez ? Tous les points d'une courbe sous les yeux ? Les assymptotes , les limites , les points d'inflexion . Une simple transformation , comme décrite dans l'image redonne les coordonnées réelles X' et UN étangs imaginaires . Quelle révolution pour les calculatrices graphiques ! Pouvoir afficher la totalité d'une courbe sur un petit écran ... On peut faire des choses fantastiques dans ce plan .
et alors ? le plan de Poincaré (Henri Poincaré 1854-1912, et ce n'est même pas lui qui a inventé ça) fait pareil et ce n'est pas nouveau, ni la seule façon de procéder.
rien de révolutionnaire donc, sans avoir le détail précis de ta représentation et de ta façon de "calculer" (sic) des valeurs sur une figure (!)
j'ai décroché des maths il y a 20 ans de ça
ça se voit : le manque de rigueur (que du baratin flou sans définitions précises) de tes écrits actuels le montre à l'évidence.
quant à tes écrits passés ils sont trop anciens pour qu'ils existent en format numérique
et je n'ai pas la collection papier complète du bulletin de l'APMEP ! je n'en dirais donc rien.
je n'en ai trouvé que le titre :
"Une génération géométrique des inverses de naturels (A. Ratomahenina)"
je suppose que c'est en lien avec ta prétendue construction de 1/5 à la règle seule de l'autre discussion
dont j'ai dit ce que j'en pensais (ce n'est pas ce que tu prétends : ce n'est pas à la règle seule, il faut en plus un outil pour tracer des perpendiculaires / parallèles etc ce qui n'est pas possible à la règle seule)
pourquoi j'en parle ici ?
parce que la (une) véritable construction à la règle seule plus un truc donné au préalable va faire intervenir ces fameux points à l'infini ramenés sur la feuille de papier :
données (il est absolument indispensable dans toute construction de définir avant tout précisément ce qui est donné, mais toi et la rigueur ...)
un segment AB
une parallèle Δ à (AB) (en bleu)
qui doit être donnée au préalable (on ne sait pas la tracer à la règle seule à partir du seul segment AB)
à construire à la règle seule : le point Q avec AQ = 1/5 AB
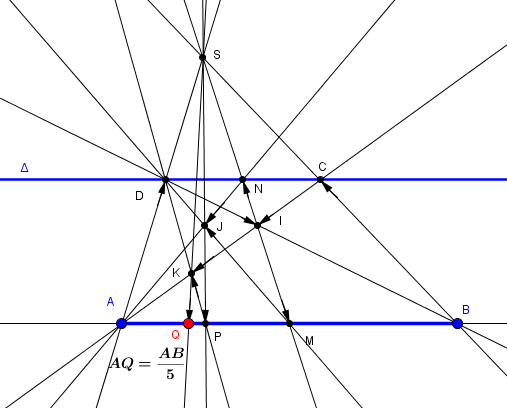
les droites et points sont tracés dans l'ordre en suivant les flèches C, D, I, M, N, J, P, K, Q
le point S est un point arbitraire décrété comme étant "le point à l'infini dans la direction perpendiculaire à (AB)"
ainsi dans cette "image" du plan, ABCD est un rectangle (si si) et on retrouve un truc du genre de ta construction mais sans tracé effectif de parallèles et de perpendiculaires impossibles à la règle seule
et sans lignes de construction planquées (tout est explicitement tracé)
la même technique permet de "construire" n'importe quel nombre rationnel, avec AB comme unité.
et ça n'a rien de nouveau (au moins du siècle dernier, voire de la Renaissance = règles de la perspective, S = "point de fuite")
je n'en ai trouvé que le titre :
"Une génération géométrique des inverses de naturels (A. Ratomahenina)"
je suppose que c'est en lien avec ta prétendue construction de 1/5 à la règle seule de l'autre discussion
dont j'ai dit ce que j'en pensais (ce n'est pas ce que tu prétends : ce n'est pas à la règle seule, il faut en plus un outil pour tracer des perpendiculaires / parallèles etc ce qui n'est pas possible à la règle seule)
Il a posté un scan sur les-maths.net