Annuler
connectez vous
- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
Résolution d'un système de 4 equations à 4 inconnues
Posté par Milkachat
Bonjour!
J'ai un petit problème pour mon DM, j'aimerais savoir si vous pouviez m'aider.
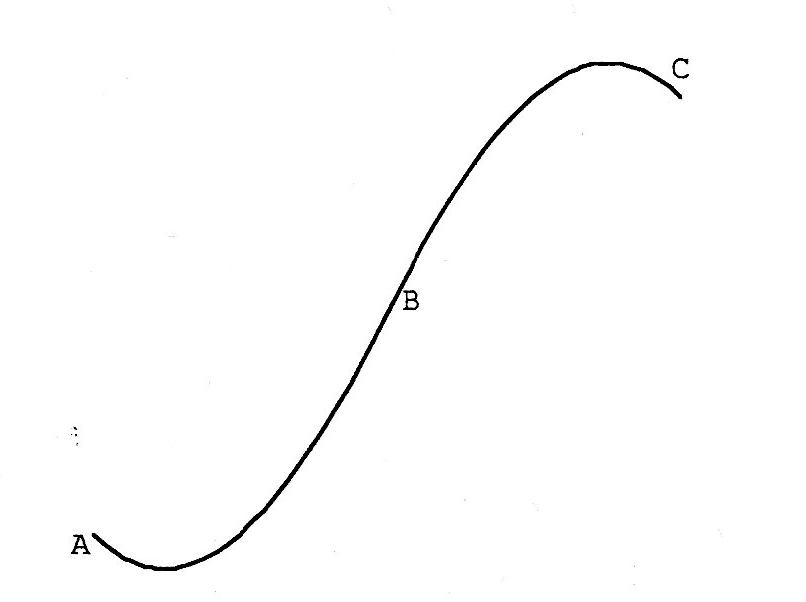
On souhaite réaliser un profil du type de celui-ci ( Voir image. )
Pour l'arc AB: Les points A et B sont imposés ( A (1;0) et B (3;3) ) ainsi que les coefficients directeurs des tangentes en ces points: -1 en A et 1 en B.
Il s'agit de déterminer une fonction f, polynôme du troisième degré satisfaisant à ces contraintes. Pour cela on sera amené à résoudre un système de 4 équations à 4 inconnues, ce qui devra être fait conformément à la méthode décrite page 367 (Il s'agit de résoudre un système linéaire par la méthode de Gauss ) .
Donc mon problème est que je ne comprend pas comment trouver les 4 équations à partir de ce qu'on a déjà, et quelles seraient les 4 inconnues ? Car dans le livre il n'y en a que 3, et les équations sont déjà données.
Donc si vous pouviez m'aider ! 
Merci beaucoup .
Bonjour
f(x) = ax^3 + bx² + cx + d : 4 inconnues
Citation :
Les points A et B sont imposés ( A (1;0) et B (3;3) ) ainsi que les coefficients directeurs des tangentes en ces points: -1 en A et 1 en B.
Les points A et B sont imposés ( A (1;0) et B (3;3) ) ainsi que les coefficients directeurs des tangentes en ces points: -1 en A et 1 en B.
f(1) = 0 (passer par A), f(3)=3 (passer par B),
f'(1)=-1, f'(3)=1 (les coeffs directeurs des tangentes)
voilà pour les 4 équations
Soit f(x) = ax³ + bx² + cx + d avec x compris dans [1 ; 3] la fonction représentant la partie AB de la courbe.
f '(x) = 3ax² + 2bx + c.
Les contraintes de l'énoncé permettent d'écrire:
f(1)=0
f(3) = 3
f '(1) = -1
f '(3) = 1
a + b + c + d = 0
27a + 9b + 3c + d = 3
3a + 2b + c = -1
27a + 6b + c = 1
Système qu'il suffit de résoudre ...
On trouve: a = -0,75 ; b = 5 ; c = -8,75 et d = 4,5
Donc la fonction représentant la partie AB de la courbe est : f(x) = -0,75.x³ + 5.x² - 8,75.x + 4,5 pour x dans [1 ; 3]
-----
Sauf distraction.
Super !!! Merci beaucoup pour la rapidité de vos réponses!
J'ai juste une dernière question, comment faites vous pour trouver f'(1)=-1 et f'(3)=1 ??
Encore merci !
Essaie de retrouver dans ton cours ce qu'implique :
"les coefficients directeurs des tangentes en ces points: -1 en A(1;0) et 1 en B(3;3)".
Et quand tu auras trouvé, tu comprendras d'où viennent:
f'(1)=-1 et f'(3)=1
La méthode de Gauss est une "technique" parmi plein d'autres qui permet de trouver les solutions d'un système d'équations tel que celui trouvé auquel on arrive dans cet exercice.
Je suppose que tu as vu cette "méthode" au cours et il faut donc que tu l'appliques à la résolution du sytème :
a + b + c + d = 0
27a + 9b + 3c + d = 3
3a + 2b + c = -1
27a + 6b + c = 1
Je t'ai donné les solutions ... mais il te reste à les retrouver en utilisant la méthode imposée.
C'est bien le problème : Je n'ai PAS vu encore cette méthode en cours. Notre prof nous donne des DM spéciaux.
Mais merci, tu m'as beaucoup aidé pour cette première partie.
Bonjour. J'ai toujours un problème pour mon DM.
Alors, la question est : "Prouver que la représentation graphique Cf de f sur 
a un centre de symétrie."
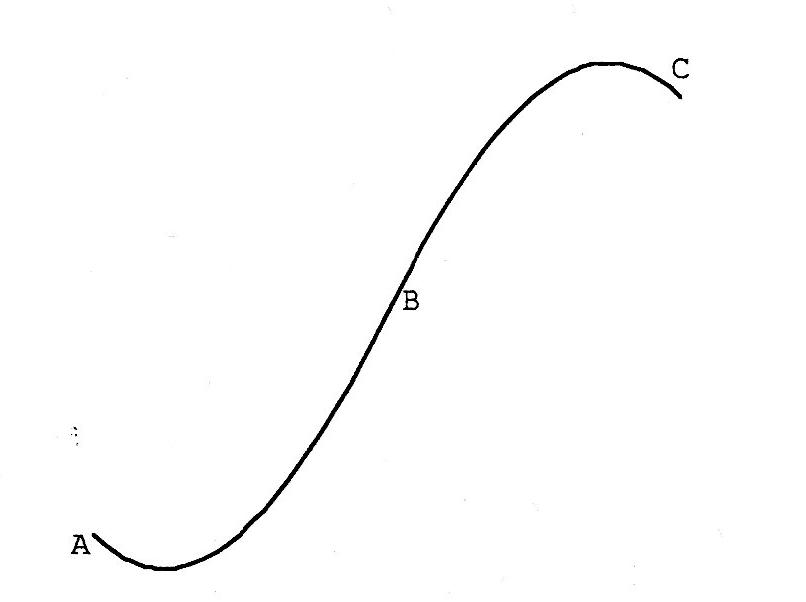
On a une courbe ( voir image ) avec A (1;0) et B (3;3). On a aussi les coefficients directeurs des tangentes en ces points: -1 en A et 1 en B.
Je ne trouve pas quel pourrait être la méthode qu'on pourrait utiliser. Si vous pouviez m'aider svp... Merci !
*** message déplacé ***
Bonjour, ca semble être le même exercice, non ?
Si oui, poursuis dans ce topic. (un topic = un exercice), merci.
On a trouvé f(x) = -0,75.x³ + 5.x² - 8,75.x + 4,5 pour x dans [1 ; 3] pour l'arc AB.
Si on étudie la fonction : f(x) = -0,75.x³ + 5.x² - 8,75.x + 4,5 pour x dans R.
---
f(a+x) = -0,75.(a+x)³ + 5(a+x)² - 8,75.(a+x) + 4,5
f(a+x) = -0,75.(a³+3a²x+3ax²+x³) + 5(a²+2ax+x²) - 8,75.a - 8,75x + 4,5
f(a-x) = -0,75.(a-x)³ + 5(a-x)² - 8,75.(a-x) + 4,5
f(a-x) = -0,75.(a³-3a²x+3ax²-x³) + 5(a²-2ax+x²) - 8,75.a + 8,75x + 4,5
f(a+x) + f(a-x) = -0,75.(a³+3a²x+3ax²+x³) + 5(a²+2ax+x²) - 8,75.a - 8,75x + 4,5 - 0,75.(a³-3a²x+3ax²-x³) + 5(a²-2ax+x²) - 8,75.a + 8,75x + 4,5
f(a+x) + f(a-x) = -0,75.(a³+3ax²) + 5(a²+x²) - 8,75.a + 4,5 - 0,75.(a³+3ax²) + 5(a²+x²) - 8,75.a + 4,5
f(a+x) + f(a-x) = -1,5.(a³+3ax²) + 10(a²+x²) - 17,5.a + 9
f(a+x) + f(a-x) = -1,5.a³ + 10a² + (10- 4,5a)x² - 17,5.a + 9
S'il y a un centre de symétrie, on peut trouver une valeur de a telle que f(a+x) + f(a-x) = K (constante) pour toute valeur de x.
--> il faut 10-4,5a = 0 (pour que f(a+x) + f(a-x) ne dépende pas de x)
a = 10/4,5 = 100/45 = 20/9
Et donc la courbe représentée par f(x) = -0,75.x³ + 5.x² - 8,75.x + 4,5 pour x dans R a un centre de symétrie, ses coordonnées sont (20/9 ; f(20/9))
-----
Sauf distraction.
Bonjour
l'énoncé a-t-il été recopié exactement au mot et à la lettre près ? le graphe de la fonction trouvée correspond tellement peu au profil , la lettre C n'intervient nullement dans les contraintes, je me pose la question !
n'était-ce pas plutôt C(3,3) ? et coeff directeurs des tangentes -1 en A et en C?
Merci beaucoup J-P !!
Citation :
Bonjour
l'énoncé a-t-il été recopié exactement au mot et à la lettre près ? le graphe de la fonction trouvée correspond tellement peu au profil , la lettre C n'intervient nullement dans les contraintes, je me pose la question !
n'était-ce pas plutôt C(3,3) ? et coeff directeurs des tangentes -1 en A et en C?
Bonjour
l'énoncé a-t-il été recopié exactement au mot et à la lettre près ? le graphe de la fonction trouvée correspond tellement peu au profil , la lettre C n'intervient nullement dans les contraintes, je me pose la question !
n'était-ce pas plutôt C(3,3) ? et coeff directeurs des tangentes -1 en A et en C?
Oui, la courbe ne représente pas ma fonction, car c'est un profil type, qui était dans l'énoncé.
Et nous n'avons aucune valeur pour C, tout a bien été recopié.
J-P, en fait je ne comprend pas ta façon de trouver le centre de symétrie, car pour moi le centre de symétrie, c'est B, et B n'a pas pour coordonnées (20/9; f(20/9) !
Salut Lafol,
Il ne faudrait s'étonner de rien.
Une moyenne de 2 erreurs par énoncé doit être assez proche de la moyenne. 
On trouverait alors (sauf erreur de ma part) que : f(x) = -1,25.x^3 + 7,5.x^2 - 12,25.x + 6 sur [1 ; 3]
Milkachat
Ce serait B si l'énoncé était celui proposé par Lafol le 23-09-10 à 10:55.
Cet énoncé est différent du tien.
Commence donc par suivre les conseils de Lafol et vérifie ton énoncé ... Plutôt 2 fois qu'une.
Moi, en utilisant la méthode de Gauss, j'avais trouvé les mêmes valeurs que tu avait trouvé au début !
Je l'ai devant moi l'énoncé, et je n'ai aucune valeur pour C !
J'ai une question 4, où il est dit " C est symétrique de A par rapport à B". N'ai-je pas des raisons de croire que B est centre de symétrie ?!
Ne pas confondre:
B est centre de symétrie de la courbe AC.
Mais B n'est pas le centre de symétrie de la courbe f(x) telle qu'on la trouve à partir de ton énoncé initial.
Or on te demande le centre de symétrie de f(x) sur R et pas le centre de symétrie de la courbe AC.
, il est plus que probable que ces 2 points (centre de symétrie de f(x) et celui de la courbe AC) devraient être les mêmes.
Ceci serait le cas si l'énoncé était "corrigé" comme l'a suggéré Lafol ...
Et c'est ce qu'on te dit et redit depuis plusieurs messages ... Il y a de fortes chances qu'il y ait une erreur dans l'énoncé initial.