Rotation d'une droite

 Niveau exercicesPartager :
			        
Rotation d'une droite
Posté par 
Alishisap  13-04-14 à 21:26
Bonjour à tous,

petit exercice niveau 2nd / 1ère dont le résultat me paraît intéressant et le but est de voir les différentes façons de résoudre ceci.

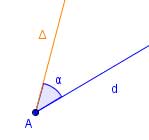
Soient une droite  et une droite  passant toutes deux par un point  et séparées d'un angle .

Question : exprimer l'équation de la droite  en fonction de , , ,  et . 
 Posté par 
Alishisapre : Rotation d'une droite  13-04-14 à 21:27
Ma réponse :

 Cliquez pour afficher
1. On prouve que la droite d forme un angle de arctan(a) avec l'axe des abscisses. On pose =+arctan(a).

2. Soit le cercle trigonométrique centré en A et B son intersection avec . On prouve que B a pour coordonnées cos+XA et sin+YA.

3. En utilisant les coordonnées de A et B on en déduit que le coefficient directeur de  est sin/cos.

4. Sachant que d et  se rejoignent en A, on résout le système d'équation qui donne accès à l'ordonnée à l'origine de .

En factorisant l'expression trouvée, on trouve finalement : 

L'intérêt de cet exercice est de voir les différentes méthodes utilisées et voir s'il est possible d'obtenir des expressions plus élégantes, peut-être sans le arctan ?

 Posté par 
idmre : Rotation d'une droite  13-04-14 à 23:51
 tu poses les question et tu y réponds... surtout que la question n'a pas grandement d'intérêt !!! 
 Posté par 
Jygzre : Rotation d'une droite  14-04-14 à 01:13
En plus  se simplifie facilement ...
 Posté par 
Alishisapre : Rotation d'une droite  14-04-14 à 13:00
Bonjour idm et Jygz,

J'ai pourtant précisé que "le but est de voir les différentes façons de résoudre ceci".

"surtout que la question n'a pas grandement d'intérêt", peut-être que pour moi si ?

Je suis juste curieux car ma méthode de résolution n'est probablement pas optimale.

Citation :

Merci, je n'avais pas remarqué. On obtient donc, de façon plus élégante :

C'est bon, laissez tomber, cette expression me satisfait et puis je ne veux pas que vous perdiez votre temps sur quelque chose qui est de toute façon trop triviale. 

Bonne journée.
 Posté par 
carpediemre : Rotation d'une droite  14-04-14 à 15:46
salut

ce n'est pas "trop trivial" même en terminale ... et même en2e/1e ce n'est pas si évident de faire le lien entre le coefficient directeur et l'angle de la droite avec (O, i) (axe des abscisses) ....

une remarque cependant :: si d est le coefficient directeur de la droite  (que tu as trouvé) alors un vecteur directeur est (1, d) et une équation de la droite est aussi :

...
 Posté par 
Imodre : Rotation d'une droite  14-04-14 à 16:03
Bonjour à tous

Il n'est d'ailleurs pas inutile de rappeler que la pente d'une droite est la tangente de l'angle qu'elle forme avec l'horizontal alors que pour une route la pente est le sinus de l'angle . Heureusement pour les petits angles les sinus et tangentes sont très voisins 

Imod

 Posté par 
Surbre : Rotation d'une droite  14-04-14 à 16:42
Bonjour,

Citation :
exprimer l'équation de la droite  en fonction de , , ,  et . 

On peut "supprimer" l'un de ces un paramètre en utilisant .

De mon côté j'ai passé l'équation sous forme paramétrique et ai multiplié cette équation par la matrice de rotation dans , lorsqu'il s'agit de revenir à une équation cartésienne ça devient vraiment pas beau (je ne suis donc pas allé jusqu'au bout)...

Je pense de plus qu'il pourrait être intéressant d'étudier le cas particulier  pour obtenir simplement  et des expressions plus "jolies" et peut-être, par la suite, "corriger" cette hypothèse par une translation.
 Posté par 
verdurinre : Rotation d'une droite  14-04-14 à 19:56
Bonsoir Imod,
Citation :
pour une route la pente est le sinus de l'angle 

je suis quasiment certain que c'est faux.

Ce n'est pas une preuve, mais on peut lire ça 
 Posté par 
Imodre : Rotation d'une droite  14-04-14 à 22:40
Tu as sans doute raison Verdurin mais on voit à peu prêt partout ( notamment dans les livrets de code de la route ) qu'une pente de 10% signifie qu'on descend de 10 m pour 100 m parcourus . D'un autre côté pour des angles petits , la distinction est assez subtile et on peut passer outre .

Imod

 Posté par 
mingrotation  17-04-14 à 22:57
Bonsoir Alishisap

 Cliquez pour afficher
Sauf qu'il y a deux droites symétriques / d puisque l'angle "" n'est pas orienté.

D'autant que tu parles ensuite de cercle trigonométrique qui lui oriente le plan.

AA+
 Posté par 
Alishisapre : Rotation d'une droite  28-04-14 à 18:25
Merci à tous, vous me donnez entière satisfaction même si je n'ai pas exactement compris la méthode de Surb  
 Posté par 
carpediemre : Rotation d'une droite  28-04-14 à 18:36
de rien

  Posté par 
Surbre : Rotation d'une droite  29-04-14 à 15:55
Citation :
si je n'ai pas exactement compris la méthode de Surb 

Dans mes souvenirs, lorsqu'on m'a appris à calculer l'image d'un point de l'espace Euclidien par une rotation de centre C, on utilisait le principe de conjugaison:

1) on fait une translation de tout l'espace pour amener C sur l'origine

2) on applique la rotation centrée sur l'origine et de même angle

3) on ramène le tout au point de départ en appliquant la translation inverse

L'avantage, c'est qu'alors il suffit d'étudier le problème pour C = 0. Mais je ne pense pas que ça apporte beaucoup vu qu'on veut revenir en cordonnées cartésiennes tôt ou tard.....