Inscription / Connexion Nouveau Sujet
Similitudes
Bonsoir,
J'ai besoin d'aide sur les deux dernières questions, voici l'énoncé :
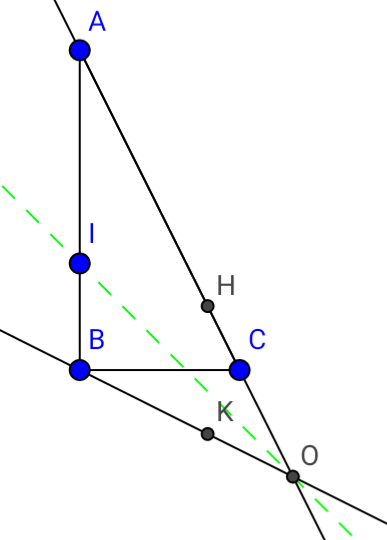
est un triangle rectangle direct en B tel que BA = 2 BC. On note H le projeté orthogonal de B sur (AC) et
Soit f la similitude directe qui envoie A sur B et B sur C
1) a) Déterminer l'angle et le rapport de f.
b) Montrer que
2) Soit la similitude indirecte qui envoie A sur B et B sur C.
a) Montrer que admet un unique point invariant O.
b) Montrer que O appartient à (AC).
3) a) Caractériser l'application .
b) En déduire que
c) Montrer que O appartient à (BK). Construire O.
4) Soit I le barycentre de (A,1) et (B,2).
a) Montrer que l'axe de est (OI)
b) Montrer que est l'intersection des droites (BC) et (OI).
Bonjour,
4)a) est la composée commutative de l' homothétie de centre
, de rapport
et de la symétrie axiale d' axe l' axe cherché ( il passe par
)
Les droites et
sont donc symétriques par rapport à cet axe.
Autrement dit, l' axe est la bissectrice intérieure de et si on appelle
son point d' intersection avec
:
Ce qui donne bien le résultat demandé.
4)b) La droite est transformée en la droite
et la droite
est globalement invariante par
...

Pour écrire çà il faut déjà qu'on ait que (OI) est la bissectrice interne de

4)a)
Les droites
Autrement dit, l' axe est la bissectrice intérieure de
La dernière égalité est bien une conséquence du fait que l' axe

Je ne sais pas si c'est correct mais je crois qu'il y a une autre méthode :
En appliquant la propriété des sinus sur les triangles AOB, AIO et BIO on devrait aboutir à =
Je crois que tu n' as pas saisi quelque chose:
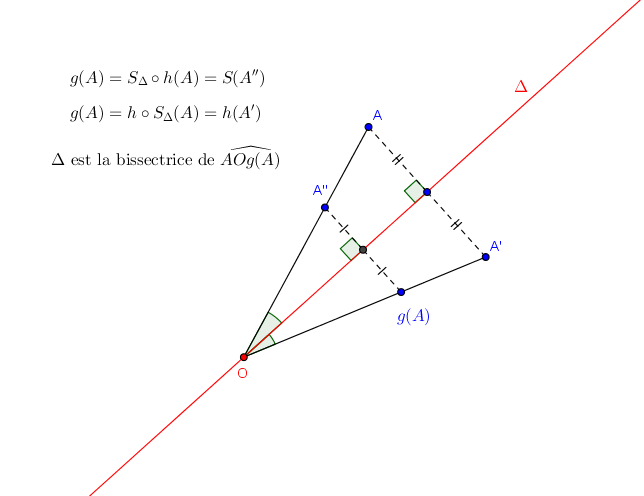
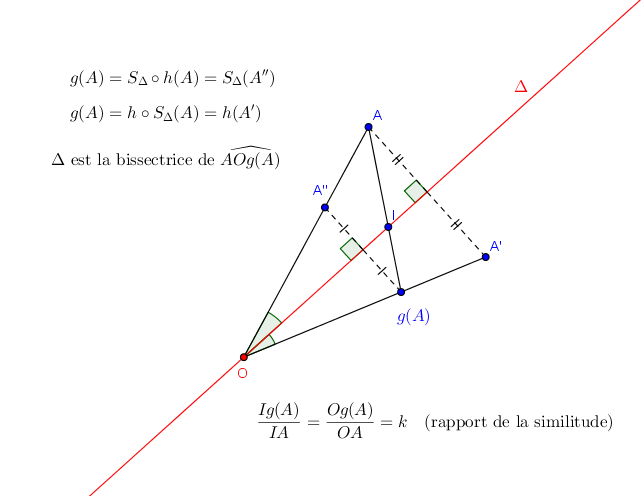
Soit une similitude indirecte de rapport différent de 1.
a un point invariant: appelons le
et un axe qui passe par
Soit un point et son image
L' axe de est la bissectrice de
Fait un dessin en utilisant où
est la symétrie axiale d' axe l' axe de
et
l' homothétie de centre
et de rapport le rapport positif de la similitude.

En fait, ce que tu as écrit en premier c'était plus simple. 
tex] et si on appelle
En effet, ça aurait été plus clair si on a choisi une lettre autre que I ( K par exemple) le point d'intersection de [AB] avec la droite portant la bissectrice puis montrer que I=K en utilisant le rapport de la similitude. C'est ce qui a créé une confusion chez moi au début.

Ah, oui! Je vois ce que tu veux dire! Quand j' ai nommé le point d' intersection , je ne pensais pas au
de l' énoncé; effectivement, j' aurais du l' appeler autrement; désolé !