Bonsoir,

A priori, pas vraiment... ^^

D'accord, c'est ce que je pensais, merci beaucoup !

Cela n'a fait que conforter mon hypothèse

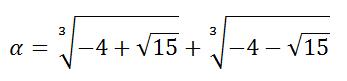
Non tu peux simplifier (voir mon fichier Proposition pdf).
Il fallait voir la formule (a+b)^3

_{* Modération > pdf supprimé car non autorisé. Merci d'utiliser les outils mis à ta disposition pour écrire les formules mathématiques *}

Salut,

Pas sûr quegermain72 te réponde (la question date de plus de 10 ans) ; cependant une remarque : on ne peut pas dire que tu as "simplifié" , dans la mesure où tu l'as exprimé en fonction de lui-même...

Bonjour lad78,
Je vois que tu es nouveau, bienvenue sur l'
A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI (Clique sur ce lien).
Prends le temps de lire ce sujet et reformule éventuellement ta réponse en respectant désormais les règles du site.

As-tu remarqué que le sujet date de 2011 ?
Et que ce que tu proposais dans ton pdf ne répond pas à la question posée : Tu trouves une équation vérifiée par , pas une simplification de l'expression de .

Bonjour Yzz,
Nous sommes bien d'accord

Salut Sylvieg !  

Bonjour, excusez moi concernant les règles du forum. Je n'ai jamais été très bons dans les règles des forum. Je ne l'ai pas fais exprès. C'est quelque chose que je maitrise mal. Après pour moi ici n'est pas une variable comme pourrait l'être x mais bien un nombre connu donc pour moi mon expression simplifiée n'est pas une équation jusqu'à preuve du contraire. Après je peux me tromper. Ce n'est pas l'affaire du siècle non plus. Le monde des mathématiques ne va pas s'écrouler non plus. Si vous pouvez me donner plus d'explication. Mais j'avais compris qu'il souhaitait une simplification de son expression. Très bonne journée à vous. Au plaisir de vous lire.

Pardon bon sans s et forum avec un s.

et explication avec un s. J'ai mal dormi cette nuit.😂

Rebonjour,
Voici un exemple où on peut simplifier :



En calculant A³ , on trouve -20 - 6A .
Le réel A est donc solution de l'équation x³+6x+20 = 0 .
Cette équation a une solution réelle simple : -2.
x³+6x+20 = (x+2)(x²-2x+10)
-2 est donc l'unique solution réelle de l'équation.
On en déduit A = -2.

Autre méthode : Chercher à écrire .

Bonjour, Merci pour votre réponse mais votre exemple est comparable à celui que j'avais repris sauf que je n'avais résolu l'équation ^3-3+8=0

"pas résolu" pardon

C'est vrai que ^3-3+8=0 n'a pas de racine évidente mais c'est possible quand même de résoudre cette équation.

A ton avis, que vas-tu trouver si tu le fais ?

J'ai bien compris. On va retomber sur l'expression du début. On tourne en rond c'est évident. Mais ma question était la suivante pourquoi quand j'exprime alpha = racine cubique de (-8 + 3 alpha) ce n'est pas la simplification de alpha = racine cubique (-4 + racine carrée 15) + racine cubique (-4 - racine carrée 15). Pour moi alpha est un nombre ce n'est pas une variable. Je l'ai juste exprimé de façon différente. Merci pour votre réponse.

Le but ici ce n'est pas de résoudre un équation qui n'a pas de sens mais de simplifier alpha en l'exprimant différemment et je pense l'avoir fait correctement avec mon expression alpha = racine cubique(-8 + 3 alpha). Et mon expression n'est pas une équation pour moi. C'est comme simplifier : 22/2

Tu l'as exprimé de façon différente, mais en fonction de lui même.
Donc ça n'apporte rien.
L'objectif est de trouver une expression numérique, c'est à dire sans inconnue.

Pour conclure : Si on résout cette équation on va retrouver le alpha du début et deux autres solutions complexe à priori.

je vous cite " Tu l'as exprimé de façon différente, mais en fonction de lui même.
Donc ça n'apporte rien.
L'objectif est de trouver une expression numérique, c'est à dire sans inconnue.
Au contraire la personne ne demandait pas un résultat exacte il voulait simplifier l'expression. Pour moi cela apporte que l'expression est plus simple. Bref de toute façon c'est un détail on ne vas pas s'attarder la dessus. Et je reviens à dire que alpha n'est pas une inconnue puisqu'il est connu dans l'expression de départ de la personne.

Dans l'équation 3x = 2.    x est bien une inconnue mais dans mon cas alpha n'est pas une inconnue. Il est juste égale à la somme de deux racines cubiques.

D'ailleurs on ne cherche pas spécialement à obtenir une valeur exacte de alpha ce n'est pas le but ici.

Non, mais une valeur numérique plus simple.