Somme nulle

 Niveau énigmesPartager :
			        
Somme nulle
Posté par 
mijo  31-08-12 à 11:24
Bonjour à tous

Compléter le carré magique de somme zéro

Dire combien de combinaisons de 5 cases donnent une somme nulle

 Posté par 
dpire : Somme nulle  31-08-12 à 14:17
Bonjour

Merci

 Cliquez pour afficher
Comme il y a 25 cases 

le 0 laisse 24 /2 12positifs et 12 négatifs

4  -8   0   8  -4

10 -7   6  -11  2

-9 -1   12  -5  3

-3  5  -12   1  9

-2  11  -6   7 -10

Il m'étonnerait qu'il y ait plusieurs solutions
 Posté par 
mijore : Somme nulle  31-08-12 à 17:58
Bonjour  dpi

C'est OK, mais la question est  combien de combinaisons de 5 cases donnent une somme nulle
 Posté par 
fontaine6140re : Somme nulle  31-08-12 à 19:40
Bonjour mijo,

 Cliquez pour afficher

Des sommes nulles de 5 éléments du carré magique unique sont au nombre de

165240=2^3 * 3^5 *5 * 17

Merci 
 Posté par 
fontaine6140re : Somme nulle  31-08-12 à 20:01

 Cliquez pour afficher

Ce n'était qu'un réponse provisoire!

Il faut enlever les doublons car l'addition est commutative!

J'y retourne...

 Posté par 
fontaine6140re : Somme nulle  31-08-12 à 22:20
 Cliquez pour afficher

Après suppression des doublons: 1141 combinaisons de 5 cases donnent une somme nulle.

 Posté par 
mijore : Somme nulle  31-08-12 à 23:19
Bonsoir  fontaine6140

Le nombre que tu annonces me laisse rêveur, je me demande si on parle de la même chose

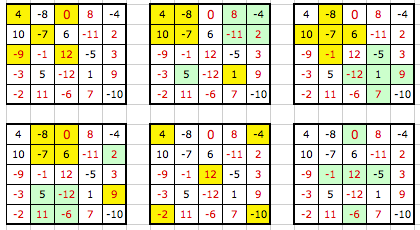
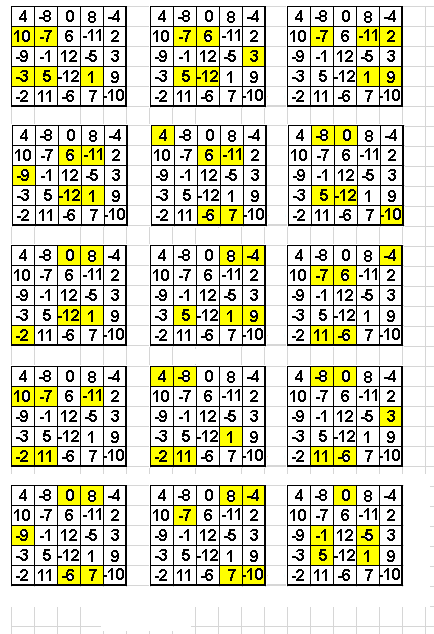
Voici quelques exemples de configurations parmi d'autres, en indiquant pour chaque combien il y a de combinaisons

 Cliquez pour afficher
 Posté par 
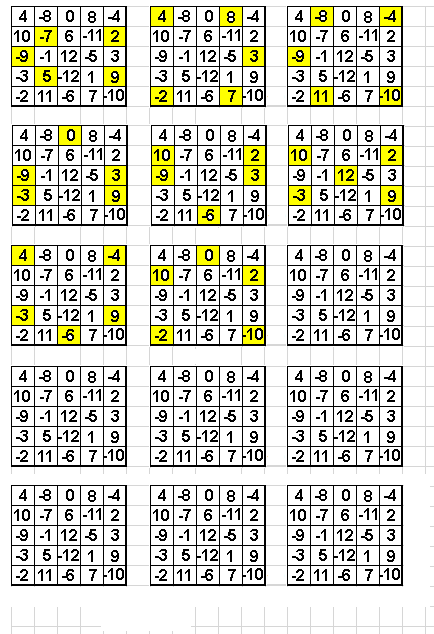
dpire : Somme nulle  01-09-12 à 09:04
Bonjour

Je pensais que tu demandais le nombre de grilles valables

Je n'en voyais qu'une :la nôtre.

 Cliquez pour afficher
Comme les seuls totaux possible positifs ou négatifs vont de 

3 à 23 il suffit de faire le tableau des possibilités .

Par exemple pour 3 positifs + 2 négatifs 705 possibilités

(et par symétrie autant pour 3 négatifs et 2 positifs)

Par contre pour 1 et 4 le nombre se réduit assez vite avec 0--> 65 possibilités

avce 1--> 16  avec 2--> 4 et 3--> 1 et autant par symétrie

en récapitulant 705+705+65+65+16+16+5+5

j'arrive à 1582 quintuplets
 Posté par 
fontaine6140re : Somme nulle  01-09-12 à 12:55
Bonjour,

 Cliquez pour afficher

Une erreur s'est glissée (ce ne sera pas la dernière!).

(J'ai mis 2 fois le nombre -9 dans le tableau).

Après correction:

On trouve 1394 quintuples de cases dans le somme vaut 0.

Les quintuples sont de la forme (a,b,c,d,e) 

avec a<b<c<d<e.

1 quintuple commence par -2

6                        -3

23                       -4

52                       -5

91                       -6

132                      -7

174                      -8

204                      -9

228                      -10

238                      -11

244                      -12

Par ex

 1366=>IJKMV : (-4)+(-3)+(-2)+( 0)+ 9= 0

 1367=>IJKNU : (-4)+(-3)+(-2)+( 1)+ 8= 0

 1368=>IJKOT : (-4)+(-3)+(-2)+( 2)+ 7= 0

 1369=>IJKPS : (-4)+(-3)+(-2)+( 3)+ 6= 0

 1370=>IJKQR : (-4)+(-3)+(-2)+( 4)+ 5= 0

 1371=>IJLMU : (-4)+(-3)+(-1)+( 0)+ 8= 0

 1372=>IJLNT : (-4)+(-3)+(-1)+( 1)+ 7= 0

 1373=>IJLOS : (-4)+(-3)+(-1)+( 2)+ 6= 0

 1374=>IJLPR : (-4)+(-3)+(-1)+( 3)+ 5= 0

 1375=>IJMNS : (-4)+(-3)+( 0)+( 1)+ 6= 0

 1376=>IJMOR : (-4)+(-3)+( 0)+( 2)+ 5= 0

 1377=>IJMPQ : (-4)+(-3)+( 0)+( 3)+ 4= 0

 1378=>IJNOQ : (-4)+(-3)+( 1)+( 2)+ 4= 0

 1379=>IKLMT : (-4)+(-2)+(-1)+( 0)+ 7= 0

 1380=>IKLNS : (-4)+(-2)+(-1)+( 1)+ 6= 0

 1381=>IKLOR : (-4)+(-2)+(-1)+( 2)+ 5= 0

 1382=>IKLPQ : (-4)+(-2)+(-1)+( 3)+ 4= 0

 1383=>IKMNR : (-4)+(-2)+( 0)+( 1)+ 5= 0

 1384=>IKMOQ : (-4)+(-2)+( 0)+( 2)+ 4= 0

 1385=>IKNOP : (-4)+(-2)+( 1)+( 2)+ 3= 0

 1386=>ILMNQ : (-4)+(-1)+( 0)+( 1)+ 4= 0

 1387=>ILMOP : (-4)+(-1)+( 0)+( 2)+ 3= 0

 1388=>JKLMS : (-3)+(-2)+(-1)+( 0)+ 6= 0

 1389=>JKLNR : (-3)+(-2)+(-1)+( 1)+ 5= 0

 1390=>JKLOQ : (-3)+(-2)+(-1)+( 2)+ 4= 0

 1391=>JKMNQ : (-3)+(-2)+( 0)+( 1)+ 4= 0

 1392=>JKMOP : (-3)+(-2)+( 0)+( 2)+ 3= 0

 1393=>JLMNP : (-3)+(-1)+( 0)+( 1)+ 3= 0

 1394=>KLMNO : (-2)+(-1)+( 0)+( 1)+ 2= 0

Pour la codification

I a pour code ascii 73 =>73-77=-4    

J                   74 =>74-77=-3          

K                   75 =>75-77=-2

M                   77 =>77-77=0  

V                   86 =>86-77=9

 : (-4)+(-3)+(-2)+( 0)+ 9= 0

 Posté par 
mijore : Somme nulle  01-09-12 à 20:03
dpi et  fontaine6140

Vous semblez être forts en informatique, mais on ne demande pas toutes les possibilités d'obtenir 0 avec les 25 nombres

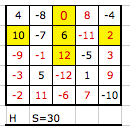
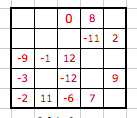
Il s'agit du nombre de configurations de 5 cases donnant 0 dans le carré. Pour plus de compréhension je joins un carré dit diabolique de Boyer à titre d'exemple

 Cliquez pour afficher
 Posté par 
fontaine6140re : Somme nulle  01-09-12 à 22:27
Il faudrait d'abord définir "configurations de 5 cases donnant 0 dans le carré".

Désolé mais je ne cerne pas ce que tu demandes.

Qu'est-ce que une configuration?

 Cliquez pour afficher

En consultant ,

la somme magique peut se trouver sur:

- les lignes

- les colonnes

- les diagonales => carré magique

- sur les parallèles aux diagonales (diagonales brisées, pandiagonales) => diabolique

- sur les sommets d'un carré intérieur aux carré initial et d'une case autre ?

(1 15 23 7 19)

- sur une croix: carré incliné à 45° et son centre (15 23 7 16 4)

mais est-ce une croix : (15 6 4 22 18)?

- étoile ???

Y en a t'il d'autres?

Merci 
 Posté par 
mijore : Somme nulle  01-09-12 à 22:51
 fontaine6140

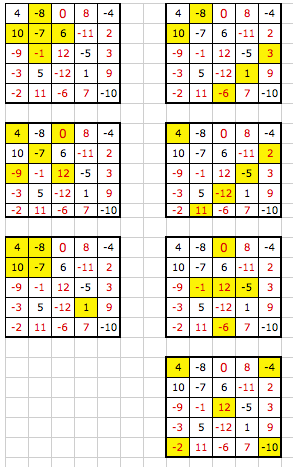
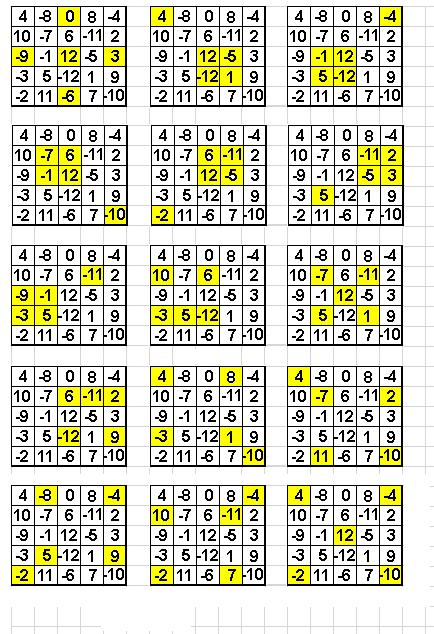
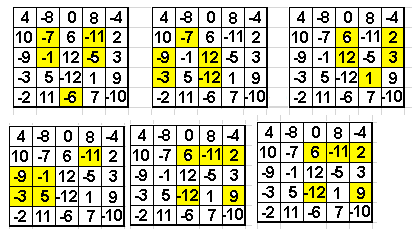
Voici les configurations que j'ai trouvé (peut-être y en a t-il d'autres), reste à savoir le nombre pour chacune d'elle.

 Cliquez pour afficher
 Posté par 
fontaine6140re : Somme nulle  01-09-12 à 23:38
Sans une définition exhaustive de la configuration,

il est impossible de programmer quelque chose de non défini. 

@+
 Posté par 
dpire : Somme nulle  02-09-12 à 09:23
Bonjour

Je suis comme fontaine6140 dérouté

car sur tes exemples on peut en rajouter

autant qu'on veut,il suffit de se donner

un objectif positif de 3 à 23 pour trouver

un négatif de -3 à-23 avec les compositions

+----, ++--- ,+++-- et ++++ -

Je pense qu'il faudrait donner une autre contrainte

par exemple "et qui se trouve dans un carré de 9 (3X3)"
 Posté par 
mijore : Somme nulle  02-09-12 à 12:05
 dpi et  fontaine6140

Je vois bien qu'on ne se comprend pas. L'énoncé du début dit "Dire combien de combinaisons de 5 cases donnent une somme nulle", j'aurais peut-être dû écrire configurations qui sont (voir mon blanké du 01-09-12 à 20:03 et celui du 01-09-12 à 22:51) carrés, étoiles, croix , pendiagonales etc...

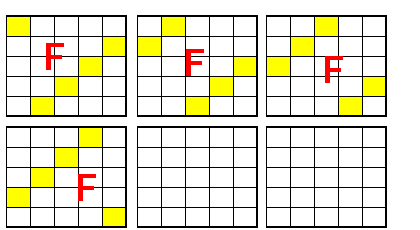
donc les possibilités que vous avez annoncées sont très au-dessus de ce que l'on peut trouver (à mon avis). Je donne un exemple avec la configuration en croix qui en donne 9 

 Cliquez pour afficher

Dites moi si c'est plus clair pour vous.
 Posté par 
fontaine6140re : Somme nulle  02-09-12 à 14:54
Non, ce n'est pas plus clair car

Citation :

... configurations qui sont carrés, étoiles, croix , pendiagonales etc...

Ce le serait s'il n'y avait pas "ETC" car

ce "etc" n'a pas de définition!!!!

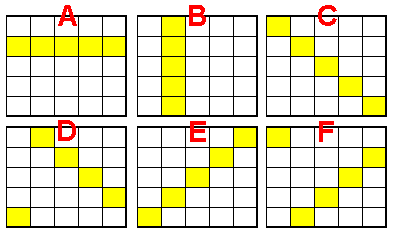
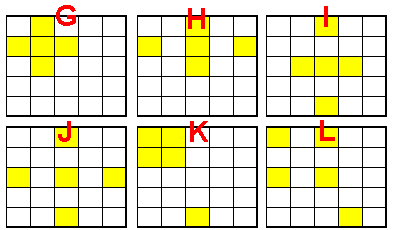
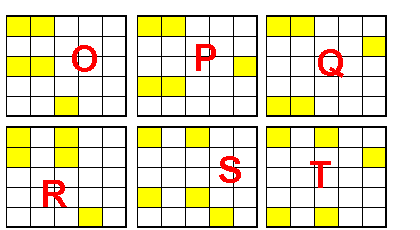
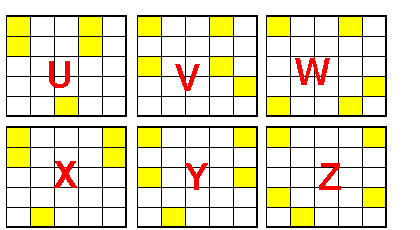
Pour poursuivre il nous faut donc dresser la liste des types de configurations admises:

Je vais commencer en les référenciant par A B C D E ...

 Cliquez pour afficher

Type A: les lignes

Type B: les colonnes

Type C: la diagonale descendante

Type D: une pandiagonale descendante

Type E: la diagonale montante

Type F: une pendiagonale montante

Type G: croix 0 (peu importe la position du sommet nord dans le carré)

Type H: croix 1h

Type I: croix 1v

Type J: croix 1h 1v

Type K: carre 0  plus une case quelconque

Type L: carre 1  plus une case quelconque

Type M: carre 2 plus une case quelconque

Type N: carre 3 plus une case quelconque

reste les rectangles 

Cette classification est-elle correcte ?
 Posté par 
dpire : Somme nulle  02-09-12 à 16:25
Je cale 

Et ce n'est pas la course de goddefroy

qui va me rendre le moral
 Posté par 
mijore : Somme nulle  03-09-12 à 12:04
Bonjour à vous deux

J'ai dû m'absenter, mais je reviens

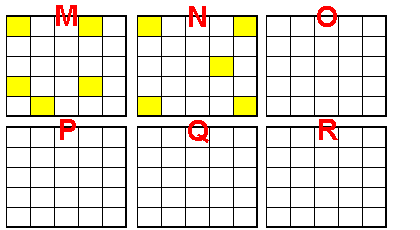
 fontaine6140 pour ta classification c'est presque bon mais tu as oublié les pendiagonales 2+3 et tes configurations M et N ne donnent pas une somme égale à 0

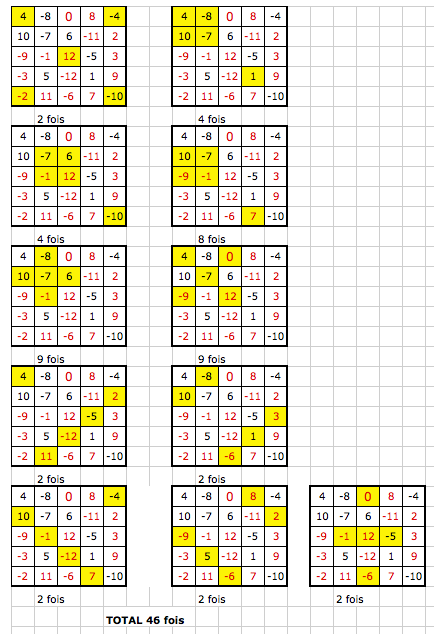
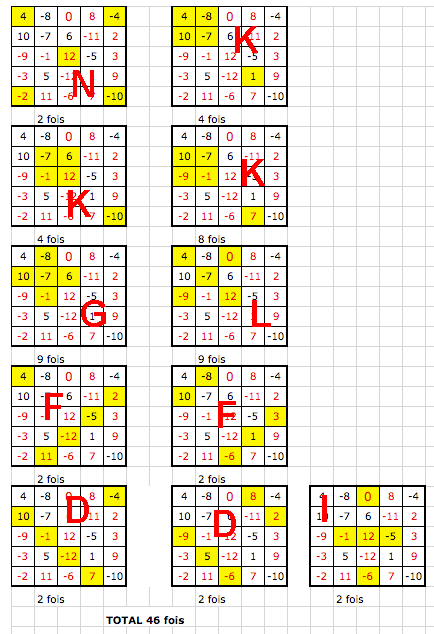
Pour ce problème , je voulais voir si mon carré est diabolique, en comparant avec celui de Boyer (voir blanké du 01-09-12 à 20:03)

Au lieu de 56 fois la somme magique je trouve 58 fois en y incluant les 12 normales pour tout carré magique d'ordre 5 (lignes, colonnes et diagonales)

sauf distraction

 Cliquez pour afficher
 Posté par 
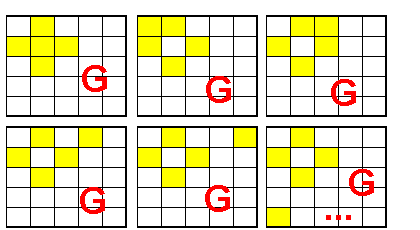
fontaine6140re : Somme nulle  03-09-12 à 12:51
Bonjour mijo,

 Cliquez pour afficher

Si je continue à blanker,c' est pour la place occupée par les images.

cela va de soi que pour le type D

pour le type F

Selon ces divers types:

 Posté par 
fontaine6140re : Somme nulle  03-09-12 à 12:53
 Cliquez pour afficher

Mais il me reste un doute sur les types G,H,I,J:

la 5è case doit-elle être située au centre ou cela peut-il être une case quelconque?

????

 Posté par 
mijore : Somme nulle  03-09-12 à 23:26
 fontaine6140

Je ne comprends pas tes doutes pour le G, seule la croix à gauche donne une somme 0, ce n'est pas le cas des 5 autres configurations

 Cliquez pour afficher

Ta figure H n'est pas exacte 

 Cliquez pour afficher

Bonne soirée
 Posté par 
fontaine6140re : Somme nulle  04-09-12 à 09:52
Bonjour mijo,

Je n'ai jamais dit que tous les types de configurations étaient valables pour ton carré magique de somme nulle.

Ce que j'essaie de faire est de déterminer une partition ( au sens mathématique)

de tous les types de configurations reconnues comme pour un carré super-magique.

Une fois que l'on aura déterminé les divers types de configurations, j'encoderais la recherche de celles-ci (les routines ).

Voilà pourquoi je n'ai jamais mis de nombres dans les cases.

Le type H ne donne pas une somme nulle pour ce carré magique mais pourrait être une somme magique pour d'autres.

Ma recherche ne part pas d'un carré magique particulier mais doit être valable pour tout carré dont on recherche les sommes magiques.

Reste toujours les rectangles

 Cliquez pour afficher

nb blancs dans horizontal, vertical. (x,y)

La 5è case est quelconque.

O:0-1,P:0-2,Q:0-3,R:1,0,S:1-2,T:1-3

U:2-0,V:2-1,W:2-3 ( pas de 2-2 car carré)

X:3-0,Y:3-1,Y:3-2 (pas de 3-3 car carré)

What else ? 
 Posté par 
mijore : Somme nulle  04-09-12 à 12:47
Comme dirait George Clooney: nothing else

Pour les rectangles, à part 1x5 (ligne ou colonne), je ne vois pas

Bon courage pour ta recherche, j'aimerais que tu me fasses part du résultat.
 Posté par 
fontaine6140re : Somme nulle  05-09-12 à 17:43
Bonjour mijo,

Selon la classification: 68 sommes magiques.

 Cliquez pour afficher

 1 : A : =>KLMNO : (-2)+(-1)+( 0)+( 1)+ 2= 0

 2 : B : =>CHMRW : (-10)+(-5)+( 0)+( 5)+ 10= 0

 3 : C : =>AGMSY : (-12)+(-6)+( 0)+( 6)+ 12= 0

 4 : D : =>BHNTU : (-11)+(-5)+( 1)+( 7)+ 8= 0

 5 : D : =>CIOPV : (-10)+(-4)+( 2)+( 3)+ 9= 0

 6 : D : =>DJKQW : (-9)+(-3)+(-2)+( 4)+ 10= 0

 7 : D : =>EFLRX : (-8)+(-7)+(-1)+( 5)+ 11= 0

 8 : E : =>EIMQU : (-8)+(-4)+( 0)+( 4)+ 8= 0

 9 : F : =>AJNRV : (-12)+(-3)+( 1)+( 5)+ 9= 0

 10 : F : =>BFOSW : (-11)+(-7)+( 2)+( 6)+ 10= 0

 11 : F : =>CGKTX : (-10)+(-6)+(-2)+( 7)+ 11= 0

 12 : F : =>DHLPY : (-9)+(-5)+(-1)+( 3)+ 12= 0

 13 : G : =>HLMNR : (-5)+(-1)+( 0)+( 1)+ 5= 0

 14 : H : =>HKMOR : (-5)+(-2)+( 0)+( 2)+ 5= 0

 15 : I : =>CLMNW : (-10)+(-1)+( 0)+( 1)+ 10= 0

 16 : J : =>CKMOW : (-10)+(-2)+( 0)+( 2)+ 10= 0

 17 : K : =>AMNRS : (-12)+( 0)+( 1)+( 5)+ 6= 0

 18 : K : =>ELMQR : (-8)+(-1)+( 0)+( 4)+ 5= 0

 19 : K : =>GHLMY : (-6)+(-5)+(-1)+( 0)+ 12= 0

 20 : K : =>HIMNU : (-5)+(-4)+( 0)+( 1)+ 8= 0

 21 : K : =>IJNOQ : (-4)+(-3)+( 1)+( 2)+ 4= 0

 22 : K : =>IKLPQ : (-4)+(-2)+(-1)+( 3)+ 4= 0

 23 : L : =>FHPQR : (-7)+(-5)+( 3)+( 4)+ 5= 0

 24 : L : =>GIMQS : (-6)+(-4)+( 0)+( 4)+ 6= 0

 25 : L : =>HIJRT : (-5)+(-4)+(-3)+( 5)+ 7= 0

 26 : M : =>ADPSY : (-12)+(-9)+( 3)+( 6)+ 12= 0

 27 : M : =>AGJVY : (-12)+(-6)+(-3)+( 9)+ 12= 0

 28 : M : =>BEQTU : (-11)+(-8)+( 4)+( 7)+ 8= 0

 29 : M : =>EFIUX : (-8)+(-7)+(-4)+( 8)+ 11= 0

 30 : N : =>AEMUY : (-12)+(-8)+( 0)+( 8)+ 12= 0

 31 : O : =>FGPQS : (-7)+(-6)+( 3)+( 4)+ 6= 0

 32 : O : =>GHOQR : (-6)+(-5)+( 2)+( 4)+ 5= 0

 33 : O : =>GIJST : (-6)+(-4)+(-3)+( 6)+ 7= 0

 34 : O : =>HIKRS : (-5)+(-4)+(-2)+( 5)+ 6= 0

 35 : P : =>AHIWX : (-12)+(-5)+(-4)+( 10)+ 11= 0

 36 : P : =>BCQRY : (-11)+(-10)+( 4)+( 5)+ 12= 0

 37 : P : =>CDRSU : (-10)+(-9)+( 5)+( 6)+ 8= 0

 38 : P : =>DEQST : (-9)+(-8)+( 4)+( 6)+ 7= 0

 39 : P : =>EGHVW : (-8)+(-6)+(-5)+( 9)+ 10= 0

 40 : P : =>FGIUV : (-7)+(-6)+(-4)+( 8)+ 9= 0

 41 : Q : =>ABSUV : (-12)+(-11)+( 6)+( 8)+ 9= 0

 42 : Q : =>BCOVW : (-11)+(-10)+( 2)+( 9)+ 10= 0

 43 : Q : =>CDKWX : (-10)+(-9)+(-2)+( 10)+ 11= 0

 44 : Q : =>DEGXY : (-9)+(-8)+(-6)+( 11)+ 12= 0

 45 : R : =>CLNQS : (-10)+(-1)+( 1)+( 4)+ 6= 0

 46 : R : =>GILNW : (-6)+(-4)+(-1)+( 1)+ 10= 0

 47 : R : =>GKMPR : (-6)+(-2)+( 0)+( 3)+ 5= 0

 48 : R : =>HJMOS : (-5)+(-3)+( 0)+( 2)+ 6= 0

 49 : S : =>BDQSW : (-11)+(-9)+( 4)+( 6)+ 10= 0

 50 : S : =>CERST : (-10)+(-8)+( 5)+( 6)+ 7= 0

 51 : S : =>CGIVX : (-10)+(-6)+(-4)+( 9)+ 11= 0

 52 : S : =>FGHUW : (-7)+(-6)+(-5)+( 8)+ 10= 0

 53 : T : =>ACQUW : (-12)+(-10)+( 4)+( 8)+ 10= 0

 54 : T : =>BDMVX : (-11)+(-9)+( 0)+( 9)+ 11= 0

 55 : T : =>CEIWY : (-10)+(-8)+(-4)+( 10)+ 12= 0

 56 : U : =>ALOQT : (-12)+(-1)+( 2)+( 4)+ 7= 0

 57 : U : =>EKNPS : (-8)+(-2)+( 1)+( 3)+ 6= 0

 58 : U : =>FIKNY : (-7)+(-4)+(-2)+( 1)+ 12= 0

 59 : U : =>GJLOU : (-6)+(-3)+(-1)+( 2)+ 8= 0

 60 : V : =>FIOPS : (-7)+(-4)+( 2)+( 3)+ 6= 0

 61 : V : =>GJKQT : (-6)+(-3)+(-2)+( 4)+ 7= 0

 62 : W : =>ADOUX : (-12)+(-9)+( 2)+( 8)+ 11= 0

 63 : W : =>BEKVY : (-11)+(-8)+(-2)+( 9)+ 12= 0

 64 : X : =>CKOPT : (-10)+(-2)+( 2)+( 3)+ 7= 0

 65 : X : =>FJKOW : (-7)+(-3)+(-2)+( 2)+ 10= 0

 66 : Y : =>FJMPT : (-7)+(-3)+( 0)+( 3)+ 7= 0

 67 : Z : =>AEPTW : (-12)+(-8)+( 3)+( 7)+ 10= 0

 68 : Z : =>CFJUY : (-10)+(-7)+(-3)+( 8)+ 12= 0

Ce qui donne en image:

 Posté par 
fontaine6140re : Somme nulle  05-09-12 à 17:47
 Cliquez pour afficher

Il se peut que certains types ne soient pas admis?

Mais je ne suis pas un spécialiste des carrés super-magiques.

@+
 Posté par 
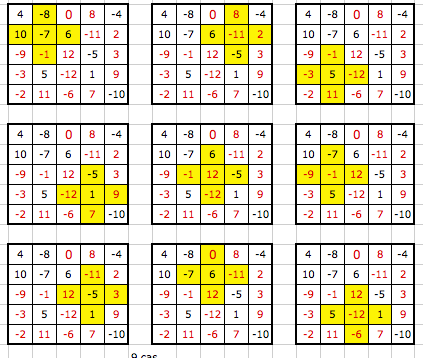
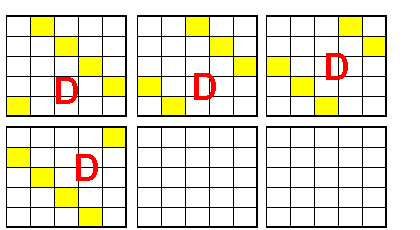
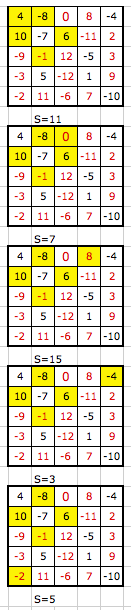
mijore : Somme nulle  05-09-12 à 19:26
Bonsoir  fontaine6140

Je n'ai jeté qu'un coup d'oeil rapide, mais il faut revoir ta copie, certains de tes carrés n'ont pas de somme 0

A titre d'exemple 

 Cliquez pour afficher
 Posté par 
fontaine6140re : Somme nulle  06-09-12 à 15:53
Bonjour mijo,

Acceptez-vous un 2è jet ?

101 sommes nulles.

 Cliquez pour afficher

Désolé pour la longueur et le graphisme.

 1 : A : =>ABCDE :  0

---------------------

|==4|=-8|==0|==8|=-4|

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 2 : A : =>FGHIJ :  0

---------------------

|===|===|===|===|===|

|=10|=-7|==6|-11|==2|

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 3 : A : =>KLMNO :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|=-9|=-1|=12|=-5|==3|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 4 : A : =>PQRST :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

|=-3|==5|-12|==1|==9|

|===|===|===|===|===|

---------------------

 5 : A : =>UVWXY :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

|=-2|=11|=-6|==7|-10|

---------------------

 6 : B : =>AFKPU :  0

---------------------

|==4|===|===|===|===|

|=10|===|===|===|===|

|=-9|===|===|===|===|

|=-3|===|===|===|===|

|=-2|===|===|===|===|

---------------------

 7 : B : =>BGLQV :  0

---------------------

|===|=-8|===|===|===|

|===|=-7|===|===|===|

|===|=-1|===|===|===|

|===|==5|===|===|===|

|===|=11|===|===|===|

---------------------

 8 : B : =>CHMRW :  0

---------------------

|===|===|==0|===|===|

|===|===|==6|===|===|

|===|===|=12|===|===|

|===|===|-12|===|===|

|===|===|=-6|===|===|

---------------------

 9 : B : =>DINSX :  0

---------------------

|===|===|===|==8|===|

|===|===|===|-11|===|

|===|===|===|=-5|===|

|===|===|===|==1|===|

|===|===|===|==7|===|

---------------------

 10 : B : =>EJOTY :  0

---------------------

|===|===|===|===|=-4|

|===|===|===|===|==2|

|===|===|===|===|==3|

|===|===|===|===|==9|

|===|===|===|===|-10|

---------------------

 11 : C : =>AGMSY :  0

---------------------

|==4|===|===|===|===|

|===|=-7|===|===|===|

|===|===|=12|===|===|

|===|===|===|==1|===|

|===|===|===|===|-10|

---------------------

 12 : D : =>BHNTU :  0

---------------------

|===|=-8|===|===|===|

|===|===|==6|===|===|

|===|===|===|=-5|===|

|===|===|===|===|==9|

|=-2|===|===|===|===|

---------------------

 13 : D : =>CIOPV :  0

---------------------

|===|===|==0|===|===|

|===|===|===|-11|===|

|===|===|===|===|==3|

|=-3|===|===|===|===|

|===|=11|===|===|===|

---------------------

 14 : D : =>DJKQW :  0

---------------------

|===|===|===|==8|===|

|===|===|===|===|==2|

|=-9|===|===|===|===|

|===|==5|===|===|===|

|===|===|=-6|===|===|

---------------------

 15 : D : =>EFLRX :  0

---------------------

|===|===|===|===|=-4|

|=10|===|===|===|===|

|===|=-1|===|===|===|

|===|===|-12|===|===|

|===|===|===|==7|===|

---------------------

 16 : E : =>EIMQU :  0

---------------------

|===|===|===|===|=-4|

|===|===|===|-11|===|

|===|===|=12|===|===|

|===|==5|===|===|===|

|=-2|===|===|===|===|

---------------------

 17 : F : =>AJNRV :  0

---------------------

|==4|===|===|===|===|

|===|===|===|===|==2|

|===|===|===|=-5|===|

|===|===|-12|===|===|

|===|=11|===|===|===|

---------------------

 18 : F : =>BFOSW :  0

---------------------

|===|=-8|===|===|===|

|=10|===|===|===|===|

|===|===|===|===|==3|

|===|===|===|==1|===|

|===|===|=-6|===|===|

---------------------

 19 : F : =>CGKTX :  0

---------------------

|===|===|==0|===|===|

|===|=-7|===|===|===|

|=-9|===|===|===|===|

|===|===|===|===|==9|

|===|===|===|==7|===|

---------------------

 20 : F : =>DHLPY :  0

---------------------

|===|===|===|==8|===|

|===|===|==6|===|===|

|===|=-1|===|===|===|

|=-3|===|===|===|===|

|===|===|===|===|-10|

---------------------

 21 : G : =>BFGHL :  0

---------------------

|===|=-8|===|===|===|

|=10|=-7|==6|===|===|

|===|=-1|===|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 22 : G : =>CGHIM :  0

---------------------

|===|===|==0|===|===|

|===|=-7|==6|-11|===|

|===|===|=12|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 23 : G : =>DHIJN :  0

---------------------

|===|===|===|==8|===|

|===|===|==6|-11|==2|

|===|===|===|=-5|===|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 24 : G : =>GKLMQ :  0

---------------------

|===|===|===|===|===|

|===|=-7|===|===|===|

|=-9|=-1|=12|===|===|

|===|==5|===|===|===|

|===|===|===|===|===|

---------------------

 25 : G : =>HLMNR :  0

---------------------

|===|===|===|===|===|

|===|===|==6|===|===|

|===|=-1|=12|=-5|===|

|===|===|-12|===|===|

|===|===|===|===|===|

---------------------

 26 : G : =>IMNOS :  0

---------------------

|===|===|===|===|===|

|===|===|===|-11|===|

|===|===|=12|=-5|==3|

|===|===|===|==1|===|

|===|===|===|===|===|

---------------------

 27 : G : =>LPQRV :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|=-1|===|===|===|

|=-3|==5|-12|===|===|

|===|=11|===|===|===|

---------------------

 28 : G : =>MQRSW :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|=12|===|===|

|===|==5|-12|==1|===|

|===|===|=-6|===|===|

---------------------

 29 : G : =>NRSTX :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|===|=-5|===|

|===|===|-12|==1|==9|

|===|===|===|==7|===|

---------------------

 30 : H : =>HKMOR :  0

---------------------

|===|===|===|===|===|

|===|===|==6|===|===|

|=-9|===|=12|===|==3|

|===|===|-12|===|===|

|===|===|===|===|===|

---------------------

 31 : H : =>MPRTW :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|=12|===|===|

|=-3|===|-12|===|==9|

|===|===|=-6|===|===|

---------------------

 32 : I : =>CLMNW :  0

---------------------

|===|===|==0|===|===|

|===|===|===|===|===|

|===|=-1|=12|=-5|===|

|===|===|===|===|===|

|===|===|=-6|===|===|

---------------------

 33 : J : =>CKMOW :  0

---------------------

|===|===|==0|===|===|

|===|===|===|===|===|

|=-9|===|=12|===|==3|

|===|===|===|===|===|

|===|===|=-6|===|===|

---------------------

 34 : K : =>ABFGS :  0

---------------------

|==4|=-8|===|===|===|

|=10|=-7|===|===|===|

|===|===|===|===|===|

|===|===|===|==1|===|

|===|===|===|===|===|

---------------------

 35 : K : =>AMNRS :  0

---------------------

|==4|===|===|===|===|

|===|===|===|===|===|

|===|===|=12|=-5|===|

|===|===|-12|==1|===|

|===|===|===|===|===|

---------------------

 36 : K : =>BCGHT :  0

---------------------

|===|=-8|==0|===|===|

|===|=-7|==6|===|===|

|===|===|===|===|===|

|===|===|===|===|==9|

|===|===|===|===|===|

---------------------

 37 : K : =>BNOST :  0

---------------------

|===|=-8|===|===|===|

|===|===|===|===|===|

|===|===|===|=-5|==3|

|===|===|===|==1|==9|

|===|===|===|===|===|

---------------------

 38 : K : =>CDHIP :  0

---------------------

|===|===|==0|==8|===|

|===|===|==6|-11|===|

|===|===|===|===|===|

|=-3|===|===|===|===|

|===|===|===|===|===|

---------------------

 39 : K : =>DEIJQ :  0

---------------------

|===|===|===|==8|=-4|

|===|===|===|-11|==2|

|===|===|===|===|===|

|===|==5|===|===|===|

|===|===|===|===|===|

---------------------

 40 : K : =>DKLPQ :  0

---------------------

|===|===|===|==8|===|

|===|===|===|===|===|

|=-9|=-1|===|===|===|

|=-3|==5|===|===|===|

|===|===|===|===|===|

---------------------

 41 : K : =>ELMQR :  0

---------------------

|===|===|===|===|=-4|

|===|===|===|===|===|

|===|=-1|=12|===|===|

|===|==5|-12|===|===|

|===|===|===|===|===|

---------------------

 42 : K : =>FGKLX :  0

---------------------

|===|===|===|===|===|

|=10|=-7|===|===|===|

|=-9|=-1|===|===|===|

|===|===|===|===|===|

|===|===|===|==7|===|

---------------------

 43 : K : =>FRSWX :  0

---------------------

|===|===|===|===|===|

|=10|===|===|===|===|

|===|===|===|===|===|

|===|===|-12|==1|===|

|===|===|=-6|==7|===|

---------------------

 44 : K : =>GHLMY :  0

---------------------

|===|===|===|===|===|

|===|=-7|==6|===|===|

|===|=-1|=12|===|===|

|===|===|===|===|===|

|===|===|===|===|-10|

---------------------

 45 : K : =>GSTXY :  0

---------------------

|===|===|===|===|===|

|===|=-7|===|===|===|

|===|===|===|===|===|

|===|===|===|==1|==9|

|===|===|===|==7|-10|

---------------------

 46 : K : =>HIMNU :  0

---------------------

|===|===|===|===|===|

|===|===|==6|-11|===|

|===|===|=12|=-5|===|

|===|===|===|===|===|

|=-2|===|===|===|===|

---------------------

 47 : K : =>IJNOV :  0

---------------------

|===|===|===|===|===|

|===|===|===|-11|==2|

|===|===|===|=-5|==3|

|===|===|===|===|===|

|===|=11|===|===|===|

---------------------

 48 : K : =>IPQUV :  0

---------------------

|===|===|===|===|===|

|===|===|===|-11|===|

|===|===|===|===|===|

|=-3|==5|===|===|===|

|=-2|=11|===|===|===|

---------------------

 49 : K : =>JQRVW :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|==2|

|===|===|===|===|===|

|===|==5|-12|===|===|

|===|=11|=-6|===|===|

---------------------

 50 : L : =>ACGKM :  0

---------------------

|==4|===|==0|===|===|

|===|=-7|===|===|===|

|=-9|===|=12|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 51 : L : =>BDHLN :  0

---------------------

|===|=-8|===|==8|===|

|===|===|==6|===|===|

|===|=-1|===|=-5|===|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 52 : L : =>CEIMO :  0

---------------------

|===|===|==0|===|=-4|

|===|===|===|-11|===|

|===|===|=12|===|==3|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 53 : L : =>FHLPR :  0

---------------------

|===|===|===|===|===|

|=10|===|==6|===|===|

|===|=-1|===|===|===|

|=-3|===|-12|===|===|

|===|===|===|===|===|

---------------------

 54 : L : =>GIMQS :  0

---------------------

|===|===|===|===|===|

|===|=-7|===|-11|===|

|===|===|=12|===|===|

|===|==5|===|==1|===|

|===|===|===|===|===|

---------------------

 55 : L : =>HJNRT :  0

---------------------

|===|===|===|===|===|

|===|===|==6|===|==2|

|===|===|===|=-5|===|

|===|===|-12|===|==9|

|===|===|===|===|===|

---------------------

 56 : L : =>KMQUW :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|=-9|===|=12|===|===|

|===|==5|===|===|===|

|=-2|===|=-6|===|===|

---------------------

 57 : L : =>LNRVX :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|=-1|===|=-5|===|

|===|===|-12|===|===|

|===|=11|===|==7|===|

---------------------

 58 : L : =>MOSWY :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|=12|===|==3|

|===|===|===|==1|===|

|===|===|=-6|===|-10|

---------------------

 59 : M : =>ADPSY :  0

---------------------

|==4|===|===|==8|===|

|===|===|===|===|===|

|===|===|===|===|===|

|=-3|===|===|==1|===|

|===|===|===|===|-10|

---------------------

 60 : M : =>AGJVY :  0

---------------------

|==4|===|===|===|===|

|===|=-7|===|===|==2|

|===|===|===|===|===|

|===|===|===|===|===|

|===|=11|===|===|-10|

---------------------

 61 : M : =>BEQTU :  0

---------------------

|===|=-8|===|===|=-4|

|===|===|===|===|===|

|===|===|===|===|===|

|===|==5|===|===|==9|

|=-2|===|===|===|===|

---------------------

 62 : M : =>EFIUX :  0

---------------------

|===|===|===|===|=-4|

|=10|===|===|-11|===|

|===|===|===|===|===|

|===|===|===|===|===|

|=-2|===|===|==7|===|

---------------------

 63 : N : =>AEMUY :  0

---------------------

|==4|===|===|===|=-4|

|===|===|===|===|===|

|===|===|=12|===|===|

|===|===|===|===|===|

|=-2|===|===|===|-10|

---------------------

 64 : O : =>BCLMP :  0

---------------------

|===|=-8|==0|===|===|

|===|===|===|===|===|

|===|=-1|=12|===|===|

|=-3|===|===|===|===|

|===|===|===|===|===|

---------------------

 65 : O : =>BMNWX :  0

---------------------

|===|=-8|===|===|===|

|===|===|===|===|===|

|===|===|=12|=-5|===|

|===|===|===|===|===|

|===|===|=-6|==7|===|

---------------------

 66 : O : =>DENOU :  0

---------------------

|===|===|===|==8|=-4|

|===|===|===|===|===|

|===|===|===|=-5|==3|

|===|===|===|===|===|

|=-2|===|===|===|===|

---------------------

 67 : O : =>DGHQR :  0

---------------------

|===|===|===|==8|===|

|===|=-7|==6|===|===|

|===|===|===|===|===|

|===|==5|-12|===|===|

|===|===|===|===|===|

---------------------

 68 : O : =>FGNPQ :  0

---------------------

|===|===|===|===|===|

|=10|=-7|===|===|===|

|===|===|===|=-5|===|

|=-3|==5|===|===|===|

|===|===|===|===|===|

---------------------

 69 : O : =>IJLST :  0

---------------------

|===|===|===|===|===|

|===|===|===|-11|==2|

|===|=-1|===|===|===|

|===|===|===|==1|==9|

|===|===|===|===|===|

---------------------

 70 : O : =>KLSUV :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|=-9|=-1|===|===|===|

|===|===|===|==1|===|

|=-2|=11|===|===|===|

---------------------

 71 : O : =>NOQXY :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|===|=-5|==3|

|===|==5|===|===|===|

|===|===|===|==7|-10|

---------------------

 72 : P : =>ABJPQ :  0

---------------------

|==4|=-8|===|===|===|

|===|===|===|===|==2|

|===|===|===|===|===|

|=-3|==5|===|===|===|

|===|===|===|===|===|

---------------------

 73 : P : =>AHIWX :  0

---------------------

|==4|===|===|===|===|

|===|===|==6|-11|===|

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|=-6|==7|===|

---------------------

 74 : P : =>CDORS :  0

---------------------

|===|===|==0|==8|===|

|===|===|===|===|===|

|===|===|===|===|==3|

|===|===|-12|==1|===|

|===|===|===|===|===|

---------------------

 75 : P : =>EGHVW :  0

---------------------

|===|===|===|===|=-4|

|===|=-7|==6|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

|===|=11|=-6|===|===|

---------------------

 76 : P : =>FGRUV :  0

---------------------

|===|===|===|===|===|

|=10|=-7|===|===|===|

|===|===|===|===|===|

|===|===|-12|===|===|

|=-2|=11|===|===|===|

---------------------

 77 : P : =>IJMXY :  0

---------------------

|===|===|===|===|===|

|===|===|===|-11|==2|

|===|===|=12|===|===|

|===|===|===|===|===|

|===|===|===|==7|-10|

---------------------

 78 : Q : =>ABNUV :  0

---------------------

|==4|=-8|===|===|===|

|===|===|===|===|===|

|===|===|===|=-5|===|

|===|===|===|===|===|

|=-2|=11|===|===|===|

---------------------

 79 : Q : =>BCOVW :  0

---------------------

|===|=-8|==0|===|===|

|===|===|===|===|===|

|===|===|===|===|==3|

|===|===|===|===|===|

|===|=11|=-6|===|===|

---------------------

 80 : Q : =>CDKWX :  0

---------------------

|===|===|==0|==8|===|

|===|===|===|===|===|

|=-9|===|===|===|===|

|===|===|===|===|===|

|===|===|=-6|==7|===|

---------------------

 81 : Q : =>DELXY :  0

---------------------

|===|===|===|==8|=-4|

|===|===|===|===|===|

|===|=-1|===|===|===|

|===|===|===|===|===|

|===|===|===|==7|-10|

---------------------

 82 : R : =>CLNQS :  0

---------------------

|===|===|==0|===|===|

|===|===|===|===|===|

|===|=-1|===|=-5|===|

|===|==5|===|==1|===|

|===|===|===|===|===|

---------------------

 83 : S : =>ACPRV :  0

---------------------

|==4|===|==0|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

|=-3|===|-12|===|===|

|===|=11|===|===|===|

---------------------

 84 : S : =>BDQSW :  0

---------------------

|===|=-8|===|==8|===|

|===|===|===|===|===|

|===|===|===|===|===|

|===|==5|===|==1|===|

|===|===|=-6|===|===|

---------------------

 85 : S : =>BFHUW :  0

---------------------

|===|=-8|===|===|===|

|=10|===|==6|===|===|

|===|===|===|===|===|

|===|===|===|===|===|

|=-2|===|=-6|===|===|

---------------------

 86 : S : =>CERTX :  0

---------------------

|===|===|==0|===|=-4|

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|-12|===|==9|

|===|===|===|==7|===|

---------------------

 87 : S : =>CGIVX :  0

---------------------

|===|===|==0|===|===|

|===|=-7|===|-11|===|

|===|===|===|===|===|

|===|===|===|===|===|

|===|=11|===|==7|===|

---------------------

 88 : S : =>DHJWY :  0

---------------------

|===|===|===|==8|===|

|===|===|==6|===|==2|

|===|===|===|===|===|

|===|===|===|===|===|

|===|===|=-6|===|-10|

---------------------

 89 : V : =>ADJKN :  0

---------------------

|==4|===|===|==8|===|

|===|===|===|===|==2|

|=-9|===|===|=-5|===|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 90 : V : =>BEFLO :  0

---------------------

|===|=-8|===|===|=-4|

|=10|===|===|===|===|

|===|=-1|===|===|==3|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 91 : V : =>FIOPS :  0

---------------------

|===|===|===|===|===|

|=10|===|===|-11|===|

|===|===|===|===|==3|

|=-3|===|===|==1|===|

|===|===|===|===|===|

---------------------

 92 : V : =>GJKQT :  0

---------------------

|===|===|===|===|===|

|===|=-7|===|===|==2|

|=-9|===|===|===|===|

|===|==5|===|===|==9|

|===|===|===|===|===|

---------------------

 93 : V : =>KNTUX :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|=-9|===|===|=-5|===|

|===|===|===|===|==9|

|=-2|===|===|==7|===|

---------------------

 94 : V : =>LOPVY :  0

---------------------

|===|===|===|===|===|

|===|===|===|===|===|

|===|=-1|===|===|==3|

|=-3|===|===|===|===|

|===|=11|===|===|-10|

---------------------

 95 : X : =>AEFJR :  0

---------------------

|==4|===|===|===|=-4|

|=10|===|===|===|==2|

|===|===|===|===|===|

|===|===|-12|===|===|

|===|===|===|===|===|

---------------------

 96 : X : =>CKOPT :  0

---------------------

|===|===|==0|===|===|

|===|===|===|===|===|

|=-9|===|===|===|==3|

|=-3|===|===|===|==9|

|===|===|===|===|===|

---------------------

 97 : X : =>FJKOW :  0

---------------------

|===|===|===|===|===|

|=10|===|===|===|==2|

|=-9|===|===|===|==3|

|===|===|===|===|===|

|===|===|=-6|===|===|

---------------------

 98 : X : =>HPTUY :  0

---------------------

|===|===|===|===|===|

|===|===|==6|===|===|

|===|===|===|===|===|

|=-3|===|===|===|==9|

|=-2|===|===|===|-10|

---------------------

 99 : Y : =>AEHKO :  0

---------------------

|==4|===|===|===|=-4|

|===|===|==6|===|===|

|=-9|===|===|===|==3|

|===|===|===|===|===|

|===|===|===|===|===|

---------------------

 100 : Z : =>AEPTW :  0

---------------------

|==4|===|===|===|=-4|

|===|===|===|===|===|

|===|===|===|===|===|

|=-3|===|===|===|==9|

|===|===|=-6|===|===|

---------------------

 101 : Z : =>CFJUY :  0

---------------------

|===|===|==0|===|===|

|=10|===|===|===|==2|

|===|===|===|===|===|

|===|===|===|===|===|

|=-2|===|===|===|-10|

---------------------

  Posté par 
mijore : Somme nulle  06-09-12 à 20:13
Bonsoir  fontaine6140

Je suis impressionné, j'en avais oublié pas mal !

Je n'ai pas le temps pour le moment de tout voir en détail, mais à première vue ça semble bon. Je vais m'y atteler plus tard.

Merci