Inscription / Connexion Nouveau Sujet
Sphère toboggan


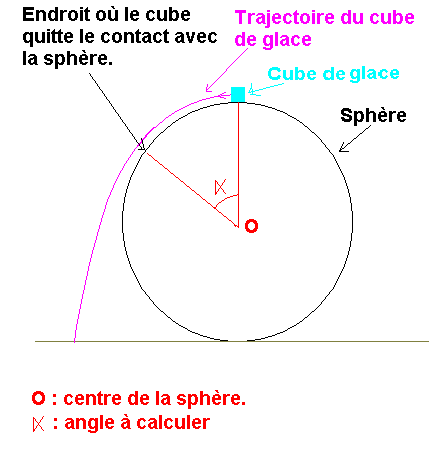
Une sphère de grand diamètre est posée sur le sol.
On pose un cube de glace de petite dimension sur le point le plus haut de la sphère.
On écarte d'une très faible distance le cube de glace en le faisant glisser sur la sphère à très petite vitesse (quasi nulle).
On abandonne alors le cube qui glisse sans rouler sur la sphère.
Quel angle (voir dessin) va parcourir le cube avant de quitter le contact avec la sphère ?
-----
On supposera les forces de frottement sur le cube nulles et les dimensions du cubes négligeables devant celles de la sphère.
L'angle sera exprimé en degrés arrondi au degré le plus proche. (le dessin n'est évidemment pas fait l'échelle  )
)
Si vous pensez que les données sont insuffisantes pour trouver la solution, indiquez "problème impossible".
-----
Bonne chance à tous. 
 En vertu du théorème de l'energie cinétique, la vitesse v acquise par le glaçon est liée au rayon r de la sphère, à l'angle a et à la gravité g par v^2/2=rg(1-cosa).
En vertu du théorème de l'energie cinétique, la vitesse v acquise par le glaçon est liée au rayon r de la sphère, à l'angle a et à la gravité g par v^2/2=rg(1-cosa).
Le glaçon décolle au moment où l'accélération centrifuge compense la composante normale du poids soit v^2/r=gcosa soit 2g(1-cosa)=gcosa ou encore cosa=2/3
Soit un angle a de 48,19 degrés (ou 0,841 radian) arrondi à 48 degrés.
Merci pour l'énigme
 Bonjour,
Bonjour,
au moment où le glaçon décolle de la sphère, sa vitesse vérifie
1/2 mv^2=r(1-cos a) mg
La réaction du support sur le glaçon est nulle (condition pour le décollement).
L'accélération normale n vérifie
n=v^2/r et mn=mg cos a
On déduit de tout ça
mg cos a = 2 mg (1-cos a)
et finalement cos a = 2/3
et a = 48°
merci 



 Salut,
Salut,
en utilisant la force centrifuge mV²/R et l energie cinetique je trouve la valeur de la force centrifuge=2gm(1-cos(alpha))
pour contrer cet force il n y a que le poids que l on projete dans la direction de la force centrifuge Pr=mg cos(alpha)
je trouve donc alpha=arccos(1/2)=60°
@+



 je me suis planté, c est arccos(2/3)=48,18°
je me suis planté, c est arccos(2/3)=48,18°



merci quand meme pour l enigme
 Salut a tous,
Salut a tous,
Le cube quittera la sphere lorsque langle alpha sera donne par:
Cos(Alpha) = 2/3 soit alpha=arccos(2/3)= 0.841068671 radians et en degres:
Alpha = 48.189 degres
Merci pour lenigme
 Rebonjour,
Rebonjour,
voici l explication plus detaillee,
2 forces ext agissant sur le cube:
Son poids et la force de contact (resp P et C)
Le theroeme de l energie cinetique dit que la variation de l NRJ cinetique pdt delta t est egale a la somme des puissances des forces ext agissant sur le systeme
Ici: travail du poids = mgR(1-cos(teta)) si teta est langle considere
pas de travail du a la force de contact (en effet, toujpours perpendiculaire au deplacement du cube)
Ds le cas ou la vitesse de depart n est pas nulle (cas general)
On arrive a
V^2-Vo^2=2*g*R*(1-cos(teta))
ensuite il reste a projetter les relations m*a=somme des forces exterierues sur les axes adequates en se rappellant bien que l acceleration NORMALE est donnee pas V^2/R
On a alors = -C+mgcos(teta)=m(V^2)/R
On remplace alors V par la valeur obtenue via le theoreme de l energie cinetique
on obtient: C=mgcos(teta)-(m/R)*(2gR(1-cos(teta)+Vo^2)
Enfin (oufff), lorque le cube quitte la sphere, C = 0, le seul alpha corresponddant a ca est donnee pas:
Cos (ALpha) = (Vo^2)/(3Rg) + 2/3
Soit avec une vitesse initiale nulle, Cos (Alpha) = 2/3
Voili
Merci pour l enigme



Bonjour.
Je serais tentée de répondre 90° intuitivement, ms bon, on verra...



De toute manière, vu mes résultats pitoyables ce mois-ci (surtout que d'habitude c'est déjà pas terrible, mais je rentre au moins dans la fin du classement!!!lol!!  ), qui ne tente rien n'a rien!!!
), qui ne tente rien n'a rien!!!
J'ai tenté de réfléchir (et oui tenté, en ce moment c'est dur!!), et je dirai qu'il nous manque des données : le diamètre de la sphère entre autre !!
Voilà, en esperant recevoir un beau smiley (ça fait super longtemps que je n'en ai pas eu!!!).
Soizic
 Salut à tous ..!!! après ces quelques semaines de repos, c'est reparti pour les énigmes...
Salut à tous ..!!! après ces quelques semaines de repos, c'est reparti pour les énigmes...
J-P !! Au risque de me répéter, je trouve toutes tes énigmes "G-é-n-i-a-l-e-s".
Elles allient à chaque fois, réflexion et astuce, mais toujours avec un énoncé simple et ... concret.
J'ai donc découvert que cet angle ne dépendant ni de g, ni de R ni de m ...étonnant non???
Comme seul le poids travaille, la variation d'énergie mécanique est nulle :
m*g*h =1/2 * m * v2
avec h =R(1-cosx)
v2= 2*g*R(1-cosx)
Dans le repère non galiléen lié au cube de glace, le déplacement perpendiculaire à la surface de la sphère est nulle.
Donc en projetant les forces sur cet axe :
m*g*cosx = T + mv2/R
soit m*g*cosx = T + 2m*g*(1-cosx) ou
T = m*g*cosx - 2m*g*(1-cosx) = m*g*(3cosx -2)
Pour que la sphère décolle, il faut que T<=0
Soit cosx <= 2/3
L'angle où le cube va quitte le contact est donc égal à arccos 2/3 = 48,189 ° soit 48 °



 Salut,
Salut,
On applique le theoreme de l'energie cinetique, et l'egalite entre la somme des forces vectorielles et la masse fois l'acceleration.
je vosu passe les calculs (le travail de la reaction normale du cylindre etant nulle, on trouve la vitesse de la bille en fonction de l'angle tant qu'elle n'a pas quitte le cylindre, et on reporte cette expression dans l'equation faisant intervenir la valeur de la reaction normale...)
Au final, la reaction devient nulle lorsque le cosinus de l'angle vaut 2/3.
DOnc le glacon decolle pour
alpha = 48 degres (48,19 arrondi au degre le plus proche par defaut)
A+
biondo
Nombre de participations : 0
Temps de réponse moyen : 27:50:02.



