Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Suite et triangle Pascal

Posté par Profil etudiantilois 26-10-18 à 17:48

Bonsoir,

J'ai des difficultés avec le début d'un DM :

                                                                                  n-1
pour tout n supérieur ou égal à 1, Fn= (n-1-k              k) (coefficient binomial)
                                                                                  k=0

1.a. Construire les dix premières lignes du triangle de Pascal.
b. Dans le triangle de Pascal précédent, pour chaque valeur de l'entier n de 1 à 10, regrouper, en les entourant, tous les coefficients binomiaux qui apparaissent dans la somme Fn.

J'ai réussi à faire la question 1.a, mais je n'arrive pas du tout à résoudre la 1.b...

Pourriez-vous m'aider s'il vous plaît ?

Merci d'avance pour l'aide, j'en ai vraiment besoin...

Bonne soirée.

Posté par
philgr22re : Suite et triangle Pascal 26-10-18 à 17:58

Bonjour,
Ne vois tu pas apparaitre des puissances d'un certain nombre?

Posté par
mathafou Moderateurre : Suite et triangle Pascal 26-10-18 à 18:18

Bonjour

là n'est pas la question du tout !
on demande d'entourer des nombres qui sont dans le triangle de Pascal

C'est surtout identifier dans le triangle les lignes et colonnes !!

pour savoir où se trouvent les \Large \binom{p}{q} dont on parle.
(sur une ligne, une colonne , une diagonale ... )

Posté par
philgr22re : Suite et triangle Pascal 26-10-18 à 18:25

ouh là je suis allé un peu loin....

Posté par
mathafou Moderateurre : Suite et triangle Pascal 26-10-18 à 18:34

(surtout que y a pas de puissances mais avec un nom "F", pour la valeur des Fn, autre question, un truc qui commence par "F" ... une histoire de lapins ... )

Posté par
philgr22re : Suite et triangle Pascal 26-10-18 à 18:35

??????

Posté par
philgr22re : Suite et triangle Pascal 26-10-18 à 18:38

J'avais lu somme des coefficients du binome..

Posté par
mathafou Moderateurre : Suite et triangle Pascal 26-10-18 à 18:58

c'est pas n'importe lesquels
c'est ceux qui sont choisis par la formule de l'énoncé ...

nota : encore faut-il savoir où se trouvent dans le triangle de Pascal des coefficients comme

\Large\binom{n-1-k}{k} pour n = 5 et k = 3 par exemple
à savoir où est \Large\binom{1}{3} (attention ce n'est pas \Large\binom{3}{1} )

pour cela il faut considérer que le triangle est entouré d'une "mer"' de zéros...

Posté par
philgr22re : Suite et triangle Pascal 26-10-18 à 19:01

C'est justement le probleme par rapport à son enoncé...:du mal à lire Fn

Posté par
mathafou Moderateurre : Suite et triangle Pascal 26-10-18 à 19:12

d'un autre côté si on lit de travers \Large\binom{k}{n-1-k} au lieu de \Large\binom{n-1-k}{k} c'est vraiment pas grave :
on effectue juste l'addition dans l'ordre inverse des mêmes.
et le problème des termes qui valent 0 est exactement le même.

Posté par Profil etudiantiloisre : Suite et triangle Pascal 26-10-18 à 23:35

Merci beaucoup pour vos réponses.

Mais je ne vois toujours pas ce que je dois identifier pour la question 1.b, je n'y arrive pas, même en me disant qu'il faut considérer une "mer" de zéros tout autour...

Pensez-vous pouvoir m'aider svp ?

Merci.

Posté par
mathafou Moderateurre : Suite et triangle Pascal 27-10-18 à 00:27

prenons un exemple avec F5
k varie de 0 à 4

F_5 = \begin{pmatrix}4\\0\end{pmatrix} + \begin{pmatrix}3\\1\end{pmatrix} + \begin{pmatrix}2\\2\end{pmatrix}+\begin{pmatrix}1\\3\end{pmatrix}+ \begin{pmatrix}0\\4\end{pmatrix} = 1 + 3 + 1 + 0 + 0 \\
où sont ces (..) dans le triangle de Pascal ?

ils sont là
(en symboles pour mieux les repérer, ton triangle est avec les valeurs de tout ça) :

Suite et triangle Pascal

les valeurs grisées sont nulles (la "mer de zéros" autour du triangle de Pascal)
mais elles interviennent dans la somme telle qu'elle est définie dans l'exo.
il faut donc les faire figurer et les entourer.

on entourera les cases demandées avec des couleurs différentes selon les valeurs de n (sinon ça revient à tout entourer !!)

Posté par Profil etudiantiloisre : Suite et triangle Pascal 27-10-18 à 13:31

Merci pour votre réponse, c'est très clair !

Et on demande les dix premières lignes, donc c'est jusqu'à n=10 ou n=9 ?

Plutôt n=9 ?

Pour la question 1.c, je conjecture que Fn+2=Fn+1+Fn.

Ensuite on me demande de démontrer cette conjecture.

J'essaye une récurrence double, mais je bloque sur l'hérédité...

Pourriez-vous m'aider s'il vous plaît ?

Merci beaucoup.

Posté par
mathafou Moderateurre : Suite et triangle Pascal 27-10-18 à 13:57


les dix premières lignes c'est les dix premières lignes

comme ton triangle commence tout en haut par \begin{pmatrix}0\\0\end{pmatrix} la dernière ligne contiendra les \begin{pmatrix}9\\k\end{pmatrix}

et servira à calculer jusqu'à F10 inclus F_{10} = \begin{pmatrix}9\\0\end{pmatrix} +\begin{pmatrix}8\\1\end{pmatrix} +...

quant à la démonstration ...
la question précédente peut être utile :
elle illustre ce qui va se passer quand on va développer la somme F_{n+1}+F_{n} directement
en développant les Σ bien entendu, pas juste regarder le dessin,
le dessin sert à identifier dans quel ordre il faut regrouper les termes de cette somme de deux sommes pour la simplifier compte tenu de la propriété fondamentale des coefficients du triangle de Pascal :

que \begin{pmatrix}n\\k\end{pmatrix} = \begin{pmatrix}n-1\\k\end{pmatrix} + \begin{pmatrix}n-1\\k-1\end{pmatrix}

et en déduire sans même besoin de récurrence que ça fait F_{n+2}

Posté par Profil etudiantiloisre : Suite et triangle Pascal 27-10-18 à 16:53

Merci pour la réponse.

Malheureusement cela fait toute l'après-midi que je cherche à démontrer la conjecture mais je n'y arrive pas... Je cherche à faire un changement d'indice dans Fn+1 puis après faire intervenir la formule de Pascal, mais je suis vraiment bloqué...

Pourriez-vous m'aider s'il vous plaît pour cette démonstration ?

Merci beaucoup car je suis perdu et je commence à paniquer...

Posté par
mathafou Moderateurre : Suite et triangle Pascal 27-10-18 à 17:41

le guide est le dessin qu'on t'a demandé de faire

pour l'utiliser dans la démonstration, il faut remarquer que on peut grouper les termes de la somme Fn et Fn+1 par paires pour donner un terme de Fn+2 :

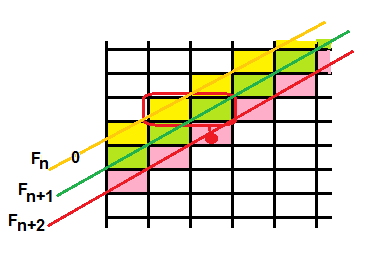
Suite et triangle Pascal

cette figure se suffit à elle même et on peut d'ores et déja considérer la démonstration comme terminée. ("preuve sans mots")

pour une démonstration plus "formelle" avec les Σ

il faut donc grouper les termes de F_n = \sum_k^{\phantom{n}} et de F_{n+1} = \sum_{k'}^{\phantom{n}} de même valeur de n-1-k et n+1-1-k'

donc k' = k+1
il n'y a pas le même nombre de termes dans Fn et dans Fn+1
on est donc amené à "extraire" des Σ les extrémités des sommes, ou à ajouter au contraire des termes dont on sait qu'ils sont nuls. (la fameuse "mer" de zéros tout autour, j'en ai montré un dans ma somme jaune Fn)

cela donne sur un exmple :

\\ F_4 = \binom{3}{0} + \binom{2}{1} + \binom{1}{2} + \binom{0}{3} \\ \\ F_5 = \binom{4}{0} + \binom{3}{1}+ \binom{2}{2}+ \binom{1}{3} + \binom{0}{4}
on ajoute ça en colonnes et en utilisant la formule de Pascal :

F_4+F_5 = \binom{4}{0} + \binom{4}{1}+ \binom{3}{2}+ \binom{2}{3} + \binom{1}{4}

et on corrige les deux bouts :

\binom{4}{0} = 1 = \binom{5}{0}

et \binom{0}{5} = 0 peut être ajouté à la fin sans vergogne :

F_4+F_5 = \binom{5}{0} + \binom{4}{1}+ \binom{3}{2}+ \binom{2}{3} + \binom{1}{4}+\binom{0}{5}

dans lequel on reconnait immédiatement F_6

formellement tout en littéral avec des k et des n et des Σ je te l'accorde c'est un peu pénible et paumatoire.

Posté par Profil etudiantiloisre : Suite et triangle Pascal 31-10-18 à 03:43

Bonjour,

Merci beaucoup pour votre réponse.

Il est 3 heures du matin, je n'arrive pas à dormir, je viens de passer la journée sur ce DM, je désespère...

Je vous donne l'énoncé complet :

Ce DM propose d'étudier la suite (Fn)n1 définie par :

n1, F_{n}=\sum_{k=0}^{n-1}{\begin{pmatrix}n-1-k\\k\end{pmatrix}}.

1. (a) Construire les dix premières lignes du triangle de Pascal.
(b) Dans le triangle de Pascal précédent, pour chaque valeur de l'entier n de 1 à 10, regrouper, en les entourant, tous les coefficients binomiaux qui apparaissent dans la somme Fn.
(c) En déduire les valeurs des dix premiers termes de la suite (Fn)n1 puis conjecturer une relation de récurrence linéaire d'ordre deux vérifiée par les termes de la suite (Fn)n1.

2. Démontrer la relation de récurrence conjecturée à la question précédente.

3. Dans un ouvrage publié en 1202 (l'un des premiers à recommander l'usage des chiffres arabes au lieu des chiffres romains), le mathématicien italien Leonardo Fibonacci a posé le problème suivant :
«En partant d'un couple de lapins nouvellement engendré, combien de couples de lapins obtient-on au bout d'une année si chaque couple engendre après deux mois d'existence un nouveau couple par mois ?»
Pour tout entier n 1, on note cn le nombre de couples de lapins au bout de n mois.
(a) Calculer les valeurs des six premiers termes de la suite (cn)n1 et comparer avec celles des premiers termes de la suite (Fn)n1. Quelle conjecture peut-on formuler ?
(b) Expliquer pourquoi la suite (cn)n1 vérifie la même relation de récurrence que la suite (Fn)n1.
(c) En déduire la réponse au problème de Fibonacci.
(d) À l'aide du résultat de la question 3(b), prouver la conjecture de la question 3(a).

4. Cette question propose de démontrer quelques propriétés de la suite (Fn)n1.
(a) À l'aide du résultat de la question 2, montrer que :
N 1, \sum_{n=1}^{N}{F_{n}}=F_{N+2}-1
(b) Exprimer le terme général Fn en fonction de l'entier n 1 et prouver que :
n1, F_{n}=\frac{1}{\sqrt{5}}(\varphi ^{n}-(-1/\varphi )^{n}). où > 1 est une constante à déterminer.
(c) À l'aide de la formule du binôme de Newton, en déduire que :
n1, F_{n}=\frac{1}{2^{n-1}}\sum_{l=0}^{\left[\frac{n-1}{2} \right]}{\begin{pmatrix}n\\2l+1\end{pmatrix}}5^{l}  (les crochets précédents correspondent à la partie entière).

5. On s'intéresse maintenant à la suite (n = Fn+1/Fn)n1 des taux de croissance mensuels du nombre de couples de lapins dans le problème originel de Fibonacci.
(a) Déterminer une fonction réelle f telle que n+1 = f(n) pour tout entier n1.
(b) Étudier les variations de f ainsi que la position relative de sa courbe représentative Cf par rapport à la droite D d'équation y = x.
(c) Sur un même graphique, représenter la courbe Cf , la droite D et les premiers termes de (n)n1.
(d) Prouver que la suite (n)n1 est bornée. Que peut-on dire à propos de sa monotonie ?
(e) Conjecturer le comportement asymptotique de la suite (n)n1 (c'est-à-dire le comportement de n quand n tend vers +) et démontrer cette conjecture à l'aide du résultat de la question 4(b).

Là où j'en suis :

C'est OK pour la question 1.

Pour la question 2, voici ce que j'ai fait :

F_{n+1}+F_{n}=\sum_{k=0}^{n}{\begin{pmatrix}n-k\\ k\end{pmatrix}}+\sum_{k=0}^{n-1}{\begin{pmatrix}n-1-k\\ k\end{pmatrix}}.

En posant l=k+1 :

F_{n+1}+F_{n}=\sum_{k=0}^{n}{\begin{pmatrix}n-k\\ k\end{pmatrix}}+\sum_{l=1}^{n}{\begin{pmatrix}n-l\\ l-1\end{pmatrix}}.

F_{n+1}+F_{n}=\sum_{k=1}^{n}{\left[\begin{pmatrix}n-k\\ k\end{pmatrix}+\begin{pmatrix}n-k\\ k-1\end{pmatrix} \right]}+\begin{pmatrix}n\\ 0\end{pmatrix}

Mais comment faire ensuite pour montrer que Fn+2=Fn+1+Fn ? Comment utiliser la formule de Pascal ? Je ne vois pas du tout...

Pour la question 3.a, j'ai : c1=1 ; c2=1 ; c3=2 ; c4=3 ; c5=5 ; c6=8. On peut conjecturer que pour tout n supérieur ou égal à 1, on a : Fn=cn.
Est-ce juste ?

Pour la question 3.b., je sens la chose mais je n'arrive pas du tout à l'expliquer... Comment faire ?

3.c et 3.d : aucune idée... J'ai cherché toute la journée et il est 3h40 du matin, je n'en peux plus... Pourriez-vous me donner un début de réponse ?

Question 4.a : je n'y arrive pas du tout non plus, je ne vois pas le lien avec la question 2... Comment pourrais-je faire ?

Merci d'avance pour l'aide, elle est indispensable...

Bonne journée.

Posté par
mathafou Moderateurre : Suite et triangle Pascal 31-10-18 à 09:11

tu y es presque

\begin{pmatrix}n-k\\ k\end{pmatrix}+\begin{pmatrix}n-k\\k-1\end{pmatrix}

c'est là qu'intervient la formule de Pascal
parce que ça c'est égal à

\begin{pmatrix}n-k+1\\ k\end{pmatrix}
et donc

F_n+F_{n+1} = \sum_{k=1}^{n}{\begin{pmatrix}n-k+1\\ k\end{pmatrix}} + \begin{pmatrix}n\\ 0\end{pmatrix}

on va maintenant réarranger un peu ça pour faire intervenir n+1 et tout mettre dans une seule somme

\begin{pmatrix}n\\ 0\end{pmatrix} = 1 = \begin{pmatrix}n+1\\ 0\end{pmatrix} c'est pareil, et on va le mettre avant la somme

on peut ajouter \begin{pmatrix}0\\ n+1\end{pmatrix} à la fin puisque c'est nul

F_n+F_{n+1} = \begin{pmatrix}n+1\\ 0\end{pmatrix} + \sum_{k=1}^{n}{\begin{pmatrix}n-k+1\\ k\end{pmatrix}} + \begin{pmatrix}0\\ n+1\end{pmatrix}

et maintenant on peut rentrer les deux termes isolés dans la somme en partant de k = 0 et en s'arrêtant à n+1 :

F_n+F_{n+1} = \sum_{k=0}^{n+1}{\begin{pmatrix}n+1-k\\ k\end{pmatrix}}
et ça y est, on a notre F_{n+2} !!

on fait en fait avec des lettres et des Σ exactement ce que j'avais fait avec mon exemple numérique qui est un guide pour voir le "cheminement"

Posté par Profil etudiantiloisre : Suite et triangle Pascal 31-10-18 à 18:04

Merci beaucoup, c'est très clair !

Avez-vous pu lire ce que j'ai dit pour les questions suivantes dans mon message de 03h43 ?

Merci encore pour l'aide.

Posté par
mathafou Moderateurre : Suite et triangle Pascal 31-10-18 à 19:39

pas trop le temps pour l'instant
mais en tout cas

question 3.a, j'ai : c1=1 ; c2=1 ; c3=2 ; c4=3 ; c5=5 ; c6=8. On peut conjecturer que pour tout n supérieur ou égal à 1, on a : Fn=cn.
Est-ce juste ?
oui si tu as fait ça directement à partir de la définition de Fibonacci

3b : c'est la même méthode que tu as dû employer pour la 3a, mais du coup "en littéral"
en supposant qu'il y a Cn , et Cn+1 l'année d'après, et en calculant Cn+2

à suivre ...

Posté par Profil etudiantiloisre : Suite et triangle Pascal 03-11-18 à 16:30

Merci beaucoup pour la réponse.

Pour la question 3.b, je sens bien la chose, mais je n'arrive pas du tout à l'expliquer en français... Comment faire ?

Ensuite je bloque à la question 4.b...

Merci encore pour l'aide.

Posté par
mathafou Moderateurre : Suite et triangle Pascal 03-11-18 à 16:45

pour ma part pour la question 3, aussi bien 3a que 3b, je fais comme ça :

je fais un tableau à trois colonnes

les vieux lapins (ceux qui procréent) les jeunes lapins (qui ne procréent pas encore) et le total (cn)


la 4b présentée comme ça brute de fonderie, ils sont gonflés
c'est un exo à part entière cette question 4b !!

tu peux toujours la jouer à l'envers c'est à dire démontrer que cette nouvelle suite définie par la formule de 4b satisfait à la relation de récurrence
et que F0 et F1 ont la bonne valeur.
donc que c'est la même suite.
quant à la valeur de φ ... tu verras bien au cours de la démonstration quelle équation doit satisfaire φ pour que ça colle.

Posté par Profil etudiantiloisre : Suite et triangle Pascal 03-11-18 à 17:14

Merci pour la réponse.

Je vais vous dire dès que possible ce que j'ai fait.

Pour la 3.d, j'ai fait une récurrence double.

Mais comment la rédiger ? Quelles sont précisément les hypothèses de récurrence ?
Et par exemple, pourquoi pourrait-on écrire dans l'hérédité que : cn+1=cn+cn-1 ?

Merci.

Posté par
mathafou Moderateurre : Suite et triangle Pascal 03-11-18 à 18:20


la 3b prouve que cn+2 = cn+1 + cn
or on a c1 = F1 et c2 = F2
donc on a cn = Fn pour tout n sans aucun besoin de rédiger une récurrence quelconque vu que deux suites qui ont la même définition sont la même suite.

Posté par Profil etudiantiloisre : Suite et triangle Pascal 04-11-18 à 16:39

J'ai réussi, merci !

Enfin, je n'arrive pas à résoudre la toute dernière question, la 5.e.

Je conjecture que la suite converge vers le nombre d'or.

Mais comment le prouver à l'aide de la question 4.b ?

Je ne vois pas du tout...

Merci d'avance pour la réponse.

Posté par Profil etudiantiloisre : Suite et triangle Pascal 04-11-18 à 17:28

up...

Merci d'avance pour l'aide. (mathafou ? malou ?)

Posté par
mathafou Moderateurre : Suite et triangle Pascal 04-11-18 à 19:11

la 4b dit que F_{n}=\frac{1}{\sqrt{5}}(\varphi ^{n}-(-1/\varphi )^{n})

écrire le rapport \dfrac{F_{n+1}}{F_n} sous la forme \varphi\dfrac{1+...}{1-...} avec les "..." qui tendront vers 0 car \varphi > 1
et donc la fraction tendra vers 1 et le rapport tendra vers \varphi

Posté par Profil etudiantiloisre : Suite et triangle Pascal 06-11-18 à 21:50

Bonsoir,

Voici donc ce que j'obtiens :

\LARGE \frac{F_{n+1}}{F_{n}}=\frac{\varphi ^{n+1}-(-\frac{1}{\varphi })^{n+1}}{\sqrt{5}}*\frac{\sqrt{5}}{\varphi ^{n}-(-\frac{1}{\varphi })^{n}}

\LARGE \frac{F_{n+1}}{F_{n}}=\frac{1-\frac{(-1)^{n+1}}{\varphi ^{2n+1}}}{1-\frac{(-1)^{n}}{\varphi ^{2n}}}

Est-ce correct ?

Si oui, comment terminer la réponse ?

Merci encore.

Posté par
mathafou Moderateurre : Suite et triangle Pascal 06-11-18 à 22:58

j'en pense que c'est faux.

tu as divisé le numérateur par \varphi^{n+1} et le dénominateur par \varphi^n

donc la fraction n'est plus égale ...
il faut remultiplier par \varphi :

\dfrac{N}{D} = \varphi\dfrac{\;\;\dfrac{N}{\varphi^{n+1}}\;}{\dfrac{D}{\varphi^n}}

Posté par Profil etudiantiloisre : Suite et triangle Pascal 06-11-18 à 23:00

Effectivement toutes mes excuses, il y avait une petite erreur de frappe, voici ce qu'il faut lire :

etudiantilois @ 06-11-2018 à 21:50

Bonsoir,

Voici donc ce que j'obtiens :

\LARGE \frac{F_{n+1}}{F_{n}}=\frac{\varphi ^{n+1}-(-\frac{1}{\varphi })^{n+1}}{\sqrt{5}}*\frac{\sqrt{5}}{\varphi ^{n}-(-\frac{1}{\varphi })^{n}}

\LARGE \frac{F_{n+1}}{F_{n}}=\varphi *\frac{1-\frac{(-1)^{n+1}}{\varphi ^{2n+1}}}{1-\frac{(-1)^{n}}{\varphi ^{2n}}}

Est-ce correct ?

Si oui, comment terminer la réponse ?

Merci encore.


C'est mieux comme ça ? Comment terminer alors ?

Posté par
mathafou Moderateurre : Suite et triangle Pascal 06-11-18 à 23:10

bein vers quoi tendent les \dfrac{1}{\varphi^k} ?
j'en ai déja parlé le 04-11-18 à 19:11

-(-1)^{n+1} = +(-1)^n d'où mon "+" de ce message là mais ça ne change rigoureusement rien du tout.

Posté par Profil etudiantiloisre : Suite et triangle Pascal 06-11-18 à 23:12

Vers 0, mais je ne sais pas du tout comment l'expliquer rigoureusement, car on aura tantôt 1 et tantôt - 1 au numérateur, n'est-ce-pas ?

Merci.

Posté par
mathafou Moderateurre : Suite et triangle Pascal 06-11-18 à 23:19

on s'en fiche des signes, du moment que la valeur absolue tend vers 0

Posté par Profil etudiantiloisre : Suite et triangle Pascal 06-11-18 à 23:26

La valeur absolue de quelle quantité ?

Posté par
mathafou Moderateurre : Suite et triangle Pascal 06-11-18 à 23:30

des \left(\dfrac{-1}{\varphi}\right)^{blabla}

Posté par Profil etudiantiloisre : Suite et triangle Pascal 06-11-18 à 23:39

OK !

Donc je dois le rédiger comment ?

Parce que je suis un peu perdu avec ces valeurs absolues finalement...

Je peux dire que lim (2n) quand n tend vers l'infini = lim (2n+1) quand n tend vers l'infini = + infini ?

C'est correct ça ? Comment faut-il le justifier ?

Posté par
mathafou Moderateurre : Suite et triangle Pascal 06-11-18 à 23:52

c'est justifié par ce que π > 1 donc cette suite géométrique φk, de raison φ > 1 est divergente

ou pour ce qui nous intéresse que 1/φ < 1 et donc la suite (1/φ)k géométrique de raison < 1 a pour limite 0

et que multiplier cette limite par +1 ou -1 ne change rien à cette limite (+0 = -0 = 0)

Posté par
mathafou Moderateurre : Suite et triangle Pascal 06-11-18 à 23:54

parce que φ > 1 (π n'a rien à faire là, faute de frappe phi sans h = pi)


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !