Inscription / Connexion Nouveau Sujet
Suite u(n+1)=(1+1/u(n))^n
Salut,
Je ne sais pas répondre à ces questions.
1/ Quelles conjectures peut-on formuler concernant cette suite ?
2/ Peut-on démontrer les résultats conjecturés ?
Bonjour,
def suite(a,n) :
u=a
for i in range(1,n) :
u=(1+1/u)**i
return usuite(1.1874523,100),suite(1.1874523,101)suite(1.1874524,100),suite(1.1874524,101)Presque la même, mais en Sagemath qui fait du calcul exact sur les rationnels (les résultats sont ensuite arrondis sous forme de décimaux) au lieu de python qui calcule avec des flottants. C'est beaucoup plus lent, on fait moins d'itérations.
%time suite(18/10,12).n(),suite(18/10,13).n()Wall time: 50.4 s
(2.20745846154200, 88.5568189370395)
%time suite(19/10,12).n(),suite(19/10,13).n()Wall time: 1min 1s
(2.04333683051260, 119.157314106765)
Du coup, GBZM, j'ai du mal à suivre :
cette valeur est-elle comprise entre 1.8 et 1.9 ou bien vaut-elle
comme ton premier message le suggère ?
Question subsidiaire : cette constante est-elle totalement "ésotérique" ou peut-on la relier à des choses "connues" ?
Le calcul exact en Sagemath ne montre pas de "changement de phase" en 1.8 et 1.9, ce que semblait indiquer le calcul en flottant sous Python, et d'après ce que tu dis le calcul en excel (pas la même précision sur les flottants) place le "changeme de pĥase" en un autre endroit.
Y a-t-il vraimenet un changement de phase et si oui, où intervient-il ?
Les calculs en flottants ne sont pas fiables, les calculs exacts sont trop longs ...
Bonjour alb12,
Tes tableaux semblent confirmer la valeur charnière de donnée par GBZM à 15h18.
Néanmoins, il y a un bémol. GBZM en qui j'ai toute confiance, a aussi écrit ceci :
Y a-t-il vraiment un changement de phase et si oui, où intervient-il ?
Les calculs en flottants ne sont pas fiables, les calculs exacts sont trop longs ...
Si je comprends bien : on n'est sûr de rien . . .

Bon, j'ai quelques petites choses à rajouter  Pour une fois que j'ai le temps
Pour une fois que j'ai le temps 
Vous arrivez assez vite dans des problèmes de précision avec des nombres énormes.
Un réflexe quand je suis dans cette situation est d'utiliser les logarithmes et effectivement, ça éclaircit les choses et simplifie les calculs (pour l'ordi pas pour le codeur  ).
).
Posons .
On a
Note: les modules math et numpy de python on tout les deux une fonction log1p(x) qui calcule avec une meilleure précision que log(1+x) quand x est proche de 0.
Calculons quelques limites:
On voit que pour grand
oscille entre
et
.
Pour ce qui de la valeur de du changement de phase, c'est un peu plus compliqué.
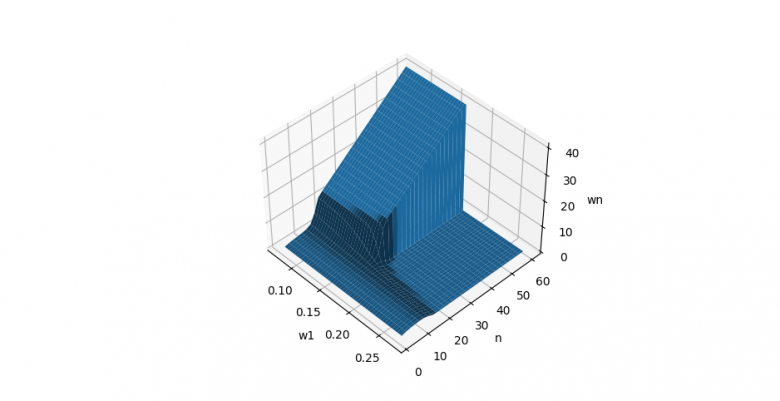
Comme on peut le voir sur le graphique ci-dessous (seul les valeurs paires de n sont représentées), le changement de phase n'apparait que quand n >> 15.
Je ne sais pas calculer mathématiquement. Mais c'est très facile d'encadrer cette valeur numériquement par bissection.
J'obtiens (
)
J'ai dû utiliser WolframAlpha pour calculer l'exponentielle, en python l'exponentielle donne la même valeur pour les deux exposants 
Il reste à caractériser la surface en fonction de . Il y a clairement un début stable puis vers n = 15 une instabilité pour arriver vers n = 25 aux deux limites.
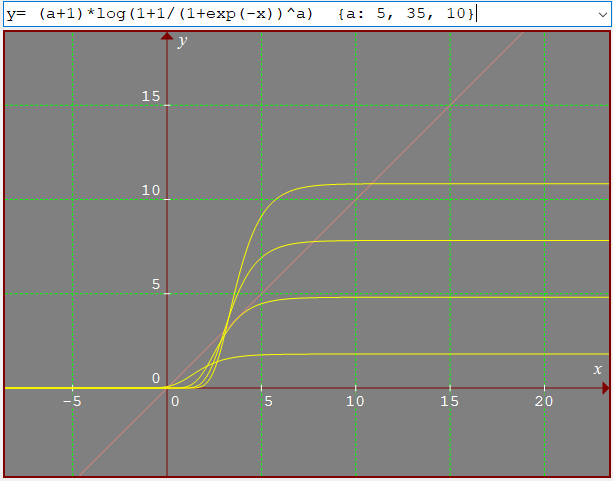
Les fonctions ressemblent à des fonctions logistique mais je ne sait pas ce que je peux faire avec ça

Sur le graphique ci-dessous () on voit que la courbe pour n = 15 en juste sous la courbe (y=x). Est-ce lié? Je n'en suis pas sûr

Je sais que la recherche d'un point fixe sur une courbe est stable quand la pente à l'intersection est < 1. Mais qu'en est-il quand on change de courbe à chaque itération?
Autre considération: peut-on trouver deux surfaces courbe continues qui enveloppent au plus près la surface ? Plus près que les deux plans
?

On peut aller plus loin en considérant .
Petit soucis, n'est pas défini, on doit commencer à
. Mais à partir de
on obtient facilement
.
On a
J'obtiens l'encadrement (
)
Analyse de :
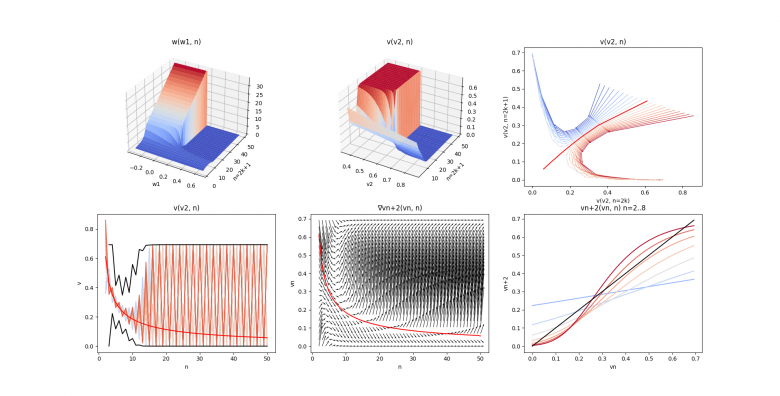
On cherche la courbe rouge. converge vers celle-ci pour
mais diverge pour
. En effet
a une pente est supérieure à 1 pour
.
Quand n augmente, on converge vers un des deux états stables .
Pour les deux surfaces enveloppant , il n'y a pas mieux que
qui sont deux surfaces irrégulières qui tendent très vite vers les deux plans
.
Vous pouvez trouver le code python que j'ai construit pour faire mes analyses ici: ![]() . Il y a surtout du code pour faire les graphiques
. Il y a surtout du code pour faire les graphiques 
Je n'ai pas fait beaucoup de conjectures et mes démonstrations sont un peu rapides mais je pense avoir apporté une bonne vision de ce quoi on a à faire 
Après quelques recherches... sur le web 
1/ Les calculs en flottants semblent justifiés ![]()
2/ L'étude de cette suite a fait l'objet de l'exercice 2 du concours general des lycees 2020 ![]()
J'espere qu'on peut trouver une demo plus courte que celle proposee par le corrige 
3/ Le programme indiqué en fin de corrige fonctionne et par exemple donne le nombre explosif entre
1.1874523511265010545954801583965193512156926815858603530
et
1.1874523511265010545954801583965193512156926815858603531
En prenant ces deux valeurs comme premier terme de la suite on obtient bien un comportement experimental conforme aux resultats theoriques.
Mouais, j'ai juste l'impression que tout mon travail est ignoré.
Le concours général des lycées démontre que v(v2, n) avec comme variable v2 est bornée, monotone. De plus max |v'(v2, n)| > c*2^n.
v(v2, n) tend donc vers une fonction échelon.
C'est assez évident dans mes réponses précédentes. Même si pas démontré proprement.
La réciproque de v(v2,n) est donc très stable. En partant d'un encadrement suffisamment petit de l'image de l'échelon, on peut inverser les calculs pour obtenir un domaine très limité. Plus limité que la précision des calculs.

 Cliquez pour afficher
Cliquez pour afficher

