Niveau énigmes

système d'équations, balance

Posté par
crabenfolie 19-06-15 à 22:07

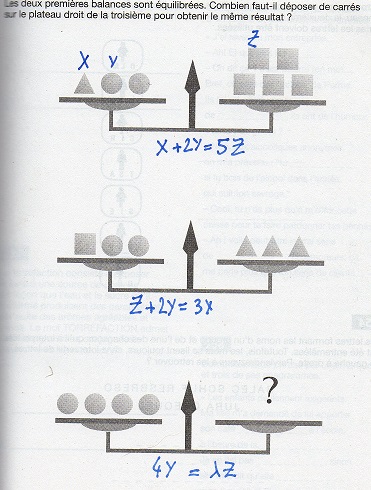
Bonjour, voilà, je suis tombé sur ce petit jeu:

Mon idée, pour trouver la solution, était de poser le système d'équations:

$\left\lbrace\begin{array}l X+2Y=5Z \\ Z+2Y=3X \\ 4Y=\lambda Z\end{array}$

En résolvant le système de manière classique, je trouve Z=7. Je me demande s'il est possible, de résoudre ce système par la méthode de Gauss, car j'ai beau essayer je n'y arrive pas, sinon pourquoi n'est-ce pas possible?

En vous remerciant par avance de votre aide.

$système d\'équations, balance$

Posté par re : système d'équations, balance 19-06-15 à 22:17

Bonjour,

que veux tu dire par je trouve Z = 7 ??? $\red\lambda$ = 7 tu veux dire ?

le système étant homogène tu ne peux pas trouver de valeurs à X, Y ni Z !!

Posté par re : système d'équations, balance 19-06-15 à 22:24

Oui plutôt désolé $\lambda =7$ .
Vous voulez dire qu'une méthode de Gauss n'a pas de sens?

Posté par re : système d'équations, balance 19-06-15 à 22:31

Bonsoir,
je ne vois pas comment trouver Z=7.

Mais il est facile de résoudre le système en fonction de Y

On a

$\begin{cases}-X+5Z=2Y\\3X-Z=2Y\end{cases}$

Posté par re : système d'équations, balance 19-06-15 à 23:42

Bonjour

sans résoudre de système (enfin ça revient au même, mais ça doit faire moins peur à la ménagère de moins de cinquante ans qui a tout oublié depuis qu'elle a quitté l'école et s'amuse avec les jeux de ce journal)

les deux premières balances ensemble : 4 ronds = 4 carrés et deux triangles (en enlevant les objets identiques qui figurent sur les deux plateaux)

on double la première balance : 4 ronds et deux triangles = 10 carrés

on additionne tout : 8 ronds = 14 carrés, donc 4 ronds = 7 carrés. (toujours en ôtant les objets identiques sur les deux plateaux)

Posté par re : système d'équations, balance 20-06-15 à 00:32

on peut aussi opérer comme suit histoire d'utiliser les équations déja écrites, que l'on peut avantageusement réordonner en :

x + 2y = 5z
3x - 2y = z

la dernière 4y = z n'étant pas une équation du tout mais étant la valeur de 4y en fonction de z cherchée !

en ajoutant membre à membre ces deux équations "bon teint" :
4x = 6z c'est à dire 2x = 3z

en multipliant par 2 la 1ere équation 2x + 4y = 10z
en substituant 2x par la valeur obtenue 3z
3z + 4y = 10z

donc 4y = 7z

en fait ce que l'on a fait ici c'est résoudre (par la méthode qu'on veut) le système de ces deux équations en les seules inconnues x et y
z étant "un paramètre", c'est à dire qu'on obtient les solutions sous la forme x = ... en fonction de z
y = en fonction de z
les calculs présentés étant organisés ici pour éviter les fractions (x = 3z/2 etc)