- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
thème : les fonctions, la partie entière
Bonjour à tous
-j'ai un petit exercice merci beaucoup d'avance
exercice: résoudre dans R
E(x)=E(x²)
ma réponse :
S=x? [(1- 5)/2;(1+
5)/2;(1+ 5)/2]
5)/2]
Bonjour, heu non ça n'est pas la solution. Comment as-tu trouvé ça ?
(par exemple x=  2 n'est pas une solution alors qu'il est dans ton intervalle et puis on voit vite qu'aucun x négatif ne peut être solution))
2 n'est pas une solution alors qu'il est dans ton intervalle et puis on voit vite qu'aucun x négatif ne peut être solution))
...
** image supprimée ** relire Q05 ![]() [lien]***
[lien]***
Bonjour,
j'aurais tenté naïvement par tâtonnement pour voir : si x < 0 alors il est clair qu'on a pas de solution (comme remarqué par Carpediem).
Si x2 > x + 1 les deux nombres sont séparés de plus que 1 donc pas de solution non plus.
Si 0 < x < 1 alors x2 < x < 1 les deux parties entières sont égales.... Ensuite on regarde ce qui reste ..
 :D
:D :D
:D
Lorsque 𝑥<0 vous avez ⌊𝑥⌋<0 tout en ayant ⌊𝑥^2⌋≥0, donc il n'y a pas de solutions négatives.
Lorsque 𝑥≥2 vous avez 𝑥^2=(𝑥−1)𝑥+𝑥≥2+𝑥 et donc ⌊𝑥⌋ est toujours au moins 2 inférieur à ⌊𝑥^2⌋ et donc il n'y a pas de solutions supérieures ou égales à 2.
Lorsque ⌊𝑥⌋=0, cela met 0≤𝑥<1 et donc ⌊𝑥^2⌋=0 aussi. Toutes les valeurs de cette plage sont des solutions.
Cela ne laisse que le cas de 𝑥∈[1,2[ à considérer. Dans cet intervalle ⌊𝑥⌋1 nous demandons donc quelles valeurs de 𝑥 dans cet intervalle ont également ⌊𝑥^2⌋=1. Cela se produit clairement quand 1≤𝑥^2<2, et quand 𝑥^2 est-il inférieur à 2 ? Quand 𝑥< 2. En effet, sur l'intervalle [1,
2. En effet, sur l'intervalle [1, 2[ on a ⌊𝑥⌋=1=^2⌋
2[ on a ⌊𝑥⌋=1=^2⌋
L'intervalle est alors [0, 2[
2[
salut
deux nombres ont même partie entière s'il appartiennent au même intervalle [n, n + 1[
donc
ce qui élimine immédiatement le cas x < 0 (pb de signe) et n  2 (car
2 (car et même
et donne immédiatement le cas (on prend 1 car
ne reste qu'à traiter le cas n = 1
posons x = 1 + d avec
....
Bonsoir,
Attention carpediem, ceci est difficile à lire :
 ).
).
Et il faudrait peut-être préciser quelque part que n est un entier.
Imiter ton "posons x = 1 + d avec
Ou se contenter d'implications pour démontrer x
 0.
0. en fait j'ai mis des accolades pour ne pas utiliser des () ou des [] déjà utiliser pour les intervalles et bien distinguer la première équivalence entre les deux propositions avec la deuxième qui est elle-même une équivalence ...
oui bien sûr mais cela est relativement évident avec ma première phrase qui sous-entend bien ce qu'est n ...
d'ailleurs j'aurai du y mettre aussi une équivalence
globalement je n'ai pas tout détailler de toute façon et seulement donner les lignes directrices (du développement) ... avec quelques détails parfois !!

de rien

Salut, je suis curieux de savoir si cette réponse est meilleure :
On a x
 E(x)
E(x)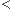 x+1
x+1
et [sup][/sup]
Oops
On a x E(x)
E(x)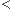 x+1
x+1
Et. x² E(x²)
E(x²)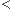 x² +1
x² +1
Alors x²-x-1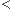 E(x²)-E(x)
E(x²)-E(x)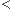 x²-x+1
x²-x+1
 x²-x-1
x²-x-1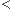 0 et 0
0 et 0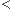 x²-x+1
x²-x+1
 (1-
(1- 5)/2
5)/2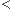 x
x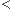 (1+
(1+ 5)/2
5)/2
Alors il y a trois probabilités
E(x)=-1
Pas vraie car : Lorsque 𝑥<0 vous avez ⌊𝑥⌋<0 tout en ayant ⌊𝑥^2⌋≥0, donc il n'y a pas de solutions négatives.
E(x)=0 : Lorsque ⌊𝑥⌋=0, cela met 0≤𝑥<1 et donc ⌊𝑥^2⌋=0 aussi. Toutes les valeurs de cette plage sont des solutions.
E(x)=1 :
posons x = 1 + d avec d [0, 1[
[0, 1[
E(x) = E(x^2) 1 = 1 + E(2d +d^2)
1 = 1 + E(2d +d^2) 0
0 2d + d^2 < 1
2d + d^2 < 1
On a d  [0;-1+
[0;-1+ 2[
2[
Alors x ]1;
]1; 2[
2[
Donc S=x [0;
[0; 2[
2[