Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Niveau exercices
Théorème de Weierstrass par les probabilités
Posté par Arkhnor
Bonjour. 
On se propose de démontrer le théorème de Weierstrass via les polynômes de Bernstein, par une méthode probabiliste.
Citation :
Soit![3$ f \, : \, [0,1] \, \to \, \mathbb{R}](https://latex.ilemaths.net/ile_tex.cgi?3$ f \, : \, [0,1] \, \to \, \mathbb{R}) continue.
continue.
1) Soit) un espace probabilisé et
un espace probabilisé et ![3$ x \in [0,1]](https://latex.ilemaths.net/ile_tex.cgi?3$ x \in [0,1]) .
.
Soit_{n \ge 1}) une suite de variables aléatoires réelles sur
une suite de variables aléatoires réelles sur 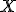 , indépendantes, et suivant la loi de Bernouilli de paramètre
, indépendantes, et suivant la loi de Bernouilli de paramètre 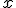 .
.
On définit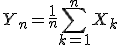 .
.
Montrer que pour tout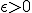 , il existe
, il existe 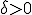 indépendant de
indépendant de  , tel que pour tout
, tel que pour tout ![3$ x \in [0,1]](https://latex.ilemaths.net/ile_tex.cgi?3$ x \in [0,1]) et tout
et tout 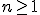 ,
,
![4$ \left{ \mathbb{E}(|f(Y_n) - f(x)| \; \mathbb{1}_{\left{|Y_n - x| < \delta\right}}) \le \epsilon \\ \mathbb{E}(|f(Y_n) - f(x)| \; \mathbb{1}_{\left{|Y_n - x| \ge \delta\right}}) \le \frac{1}{2n \delta^2}\sup_{t \in [0,1]} |f(t)|](https://latex.ilemaths.net/ile_tex.cgi?4$ \left{ \mathbb{E}(|f(Y_n) - f(x)| \; \mathbb{1}_{\left{|Y_n - x| < \delta\right}}) \le \epsilon \\ \mathbb{E}(|f(Y_n) - f(x)| \; \mathbb{1}_{\left{|Y_n - x| \ge \delta\right}}) \le \frac{1}{2n \delta^2}\sup_{t \in [0,1]} |f(t)|)
2) En déduire que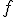 est limite uniforme sur
est limite uniforme sur ![3$ [0,1]](https://latex.ilemaths.net/ile_tex.cgi?3$ [0,1]) des polynômes de Bernstein
des polynômes de Bernstein 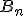 définis par
définis par  = \Bigsum_{k = 0}^n {n\choose{k}} f(\frac{k}{n})x^k (1-x)^{n-k}) ,
, ![3$ x \in [0,1]](https://latex.ilemaths.net/ile_tex.cgi?3$ x \in [0,1])
Soit
1) Soit
Soit
On définit
Montrer que pour tout
2) En déduire que
Je ne sais pas si cette démonstration est "classique", je la poste pour ceux qui ne connaissent pas.




