Inscription / Connexion Nouveau Sujet
Trajectoire d'une poulie à exprimer sous forme de fonction
Bonjour
pouvez-vous svp m'aider à résoudre cet exercice.
Le schéma ci-dessous représente un treuil pour lever des charges au moyen d'une poulie placée en C.
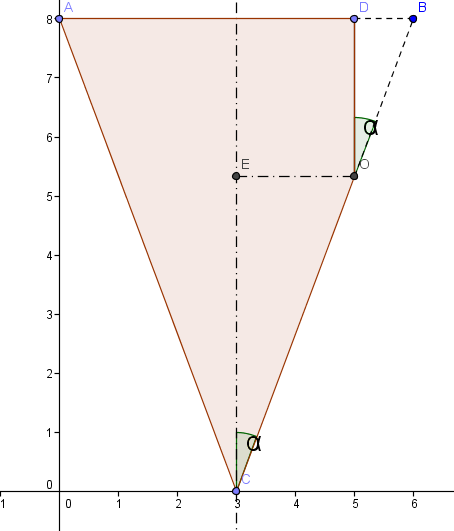
On veut déterminer une équation de la trajectoire du point C lorsque la distance EC = x varie (les rayons des poulies sont négligés).
Lorsque le point C se déplace, les angles et
nt la même mesure
 .
.
Les dimensions sont en mètres. On donne :
OE = y ; AD = 0.5 ; DO = 0.4.
1/ En exprimant tan  de deux façons différentes, déterminer une relation entre y et x.
de deux façons différentes, déterminer une relation entre y et x.
2/ au cours du déplacement on a 1 < x < 11 ; déterminer l'intervalle dans lequel varie y
3/ construire la trajectoire de la courbe représentant la fonction y = f(x).
C'est la question 1 qui me pose problème.
Je pose : et
mais je ne comprends pas comment varie DB en fonction de x.
Merci par avance pour vos explications.
Bonjour,
du déplacement de quoi ?
le mécanisme pas décrit n'est pas clair du tout...
bon, disons que A et O sont des points fixes et que la corde A-C-O a une longueur variable (ce qui fait se déplacer le point C, qui "monte" quand on raccourcit la corde)
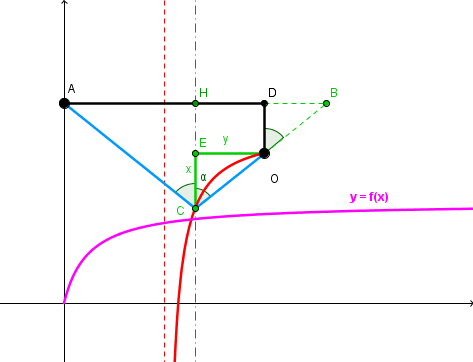
le plus simple ici est de faire intervenir le point H, milieu de [AB]
parce que AH en fonction de y est facile
et CH en fonction de x aussi
donc plutôt que d'utiliser l'angle DOB "artificiel"
on prend directement la définition de l'énoncé : angles ACH = ECO
(H milieu de AB car triangle isocèle, bissectrice = médiatrice)
ceci dit la mise en équation de l'énoncé est "loufoque" car y = f(x) n'a rien à voir avec la trajectoire de C !!
Bonjour Mathafou
merci d'avoir essayé de m'aider.
Je suis conforté dans mon sentiment que l'énoncé manque de clarté sur la partir technique que l'on veut appliquer.
En continuant à réfléchir, et à partir de tes éléments de réponse, j'aboutis à la fonction homographique :
Qu'en dis-tu ?
cela me semble bon (je trouve pareil)
quand x = 0 la poulie est en O, y = 0
quand x tend vers l'infini, la poulie se rapproche (asymptote) de la médiatrice de AD, y = 0.5/2 = 1/4
en fait le truc farfelu du choix des noms des variables prend tout son sens si on choisit comme repère le truc "antinaturel" (OX, OY) avec O centre des coordonnées
OX (abscisses) vertical dirigé vers le bas
OY (ordonnées) horizontal dirigé vers la gauche. 
alors dans ce repère la courbe représentative de f(x) est bien la trajectoire de C
Ceci dit j'ai qd même de gros doutes car qd on répond à la question 2, y varierait de de 0.208 m à 0.245 m !
Bizarre comme poulie 
>> nos messages se sont croisés ! Tes pistes et ton raisonnement me semblaient bons, je m'en suis inspiré, mais bon, je pense qu'il faut tjs avoir un regard "critique" sur les résultats et là...je reste perplexe
Après si la personne qui a rédigé l'énoncé n'est pas plus experte que cela en mécanique appliquée, pensant bien faire en montrant les applications des maths à la pratique, l'énoncé et les résultats auxquels il conduit semblent peu conformes à la réalité ! On est loin du classique "montage de résistances en parallèle" .....pour appliquer le second degré !
y varierait de de 0.208 m à 0.245 m
avec un x (la hauteur de la charge) qui varie de dix mètres
alors que l'écart horizontal entre les points fixes est de AD = 0.8 m << la distance verticale
il est "normal" que l'axe vertical (CE) de la charge C ne s'éloigne "pas trop" de la médiatrice de AD (équilibre des tensions des deux brins, donc bissectrice de ACO),
soit varie de quelques dizaines de cm (la moitié de 80 cm)
comme on s'arrête même avant (1 m avant) d'atteindre le haut (C en O), le déplacement horizontal de la charge est encore plus petit.
Mais oui!!!!!!!! c'est y (en déplacement horizontal donc) qui varie en fonction de l'élévation x de la charge. Donc oui les résultats sont plausibles!
Au temps pour moi 

 )
)
