Inscription / Connexion Nouveau Sujet
transformations planes, lieu de M?
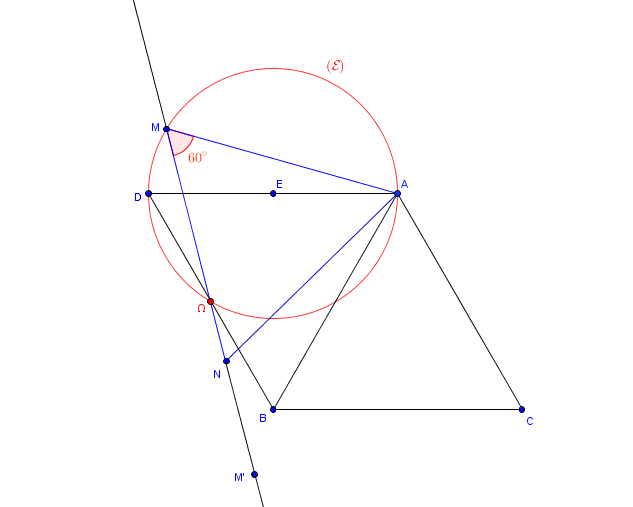
ABC est un triangle equilateral direct, on designe par r1, la rotation de centre A et d'angle 60, et r2 la rotation de centre B et d'angle 120. Pour tout point M, on pose N= r1(M) et M'=r2(M) et r=r2or1
1- a- soit D le symetrique de C par rapport a la droite (AB), determiner r(D) et r(B).
b- Demontrer que r est une symetrie centrale dont on demontra le centre w.
2-a- Montrer que l'ensemble (E) des points M tels que M,M' et N sont alignes est un cercle passant par A
et w.
b- Prouver que (E) admet AD pour diametre et que le milieu de i appartient a (E).
J'ai su faire les deux premieres parties, tres faciles, mais pas 2(a) aidez moi plzzzzzzzz 
j'ai mis cela sur le classement "college" car je n'ai pas trouve un chapitre "transformations" au lycee, je vis au liban... classe SG les maths sont un peu.... difficiles...un peu 
édit Océane : forum modifié
Ton énoncé est faux:
on pose N= r1(M) et M'=r2(M)
Non, je pense plutôt:
on pose N= r1(M) et M'=r2(N)