Niveau algorithmique

Transformée discrète de Fourier sur un nuage de points

Posté par
DreamBoy 28-04-19 à 08:47

Bien le bonjour,

Je suis élève de terminale S et je suis passionné par les maths, je viens vers vous car j'ai un soucis sur l'élaboration d'un de mes projets : Il s'agit de dessiner une figure complexe à l'aide d'épicycloïdes.
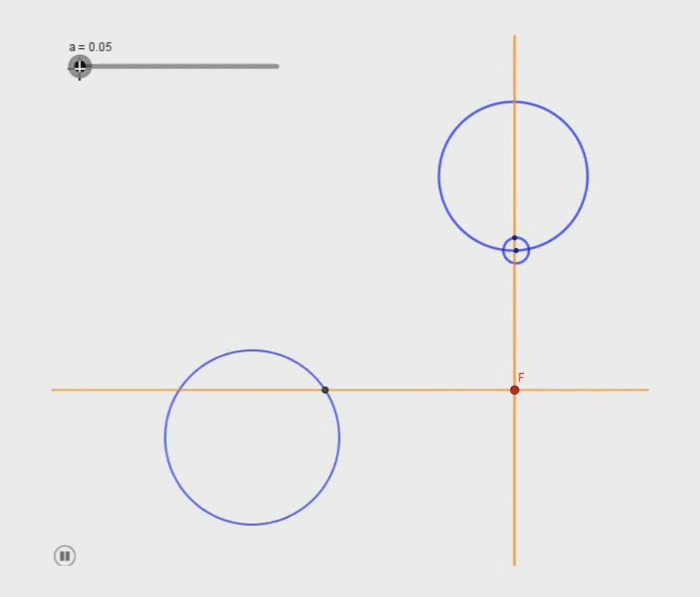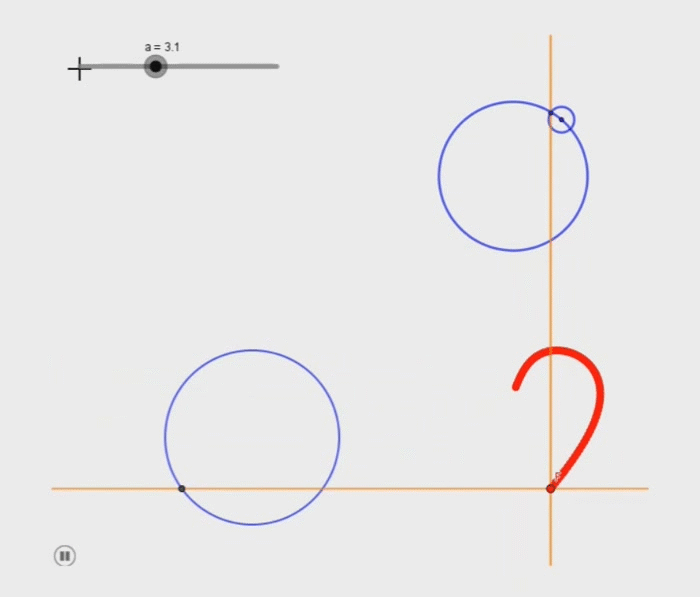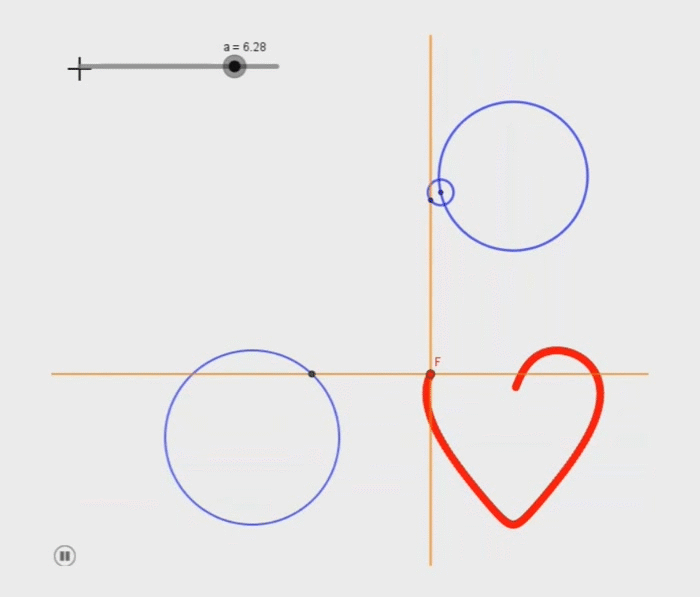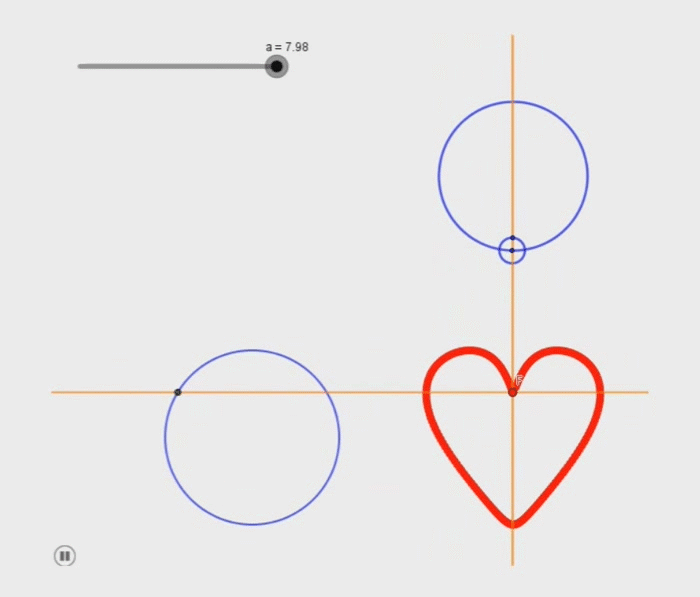
Voici ce que j'ai réussi à faire avec 3 cercles (cf image)

Pour mener à bien cela, je me suis surtout aidé de ce site : http://eljjdx.canalblog.com/archives/2018/02/15/36145181.html
Les étapes se passent merveilleusement bien mais arrive les formules sur la transformée de Fourier discrète (auxquel sur le site je ne comprends pas la notation)

J'ai tenté de me renseigner sur la TFD (je pense qu'on peut dire ceci comme cela) mais étant élève de terminale S, je n'ai pas encore un grand bagage de connaissances et je n'y comprends pas grand chose.

Pour finir, pour faire le dessin de mon coeur j'ai opté sur la régression sinusoïdale : je suis allé sur excel puis j'ai fait des regression successives et lorsque la courbe modèle ne passait pas par tout les points je faisais une régression sur "a*sin(bx+c)+d*sin(ex+f)+g" et je rajoutais une fonction avec sin jusqu'à que la courbe modèle passe par mes points.

Alors voilà ma question : comment appliquer une TFD sur un nuage de points (puisque je ne vois que des formules utilisant des intégrales de fonctions continues) ?

J'éspère que j'ai été compréhensible et je vous remercierai infiniment de votre aide.

Transformée discrète de Fourier sur un nuage de points

Posté par re : Transformée discrète de Fourier sur un nuage de points 29-04-19 à 21:09

Salut !

L'idée est donc de discrétiser ta fonction qui va de [0,T] (on prend en général $T=2\pi$ pour la périodicité des fonctions trigonométriques) dans $\mathbb{R}^2$ .
La théorie de Fourier permet de dire qu'une fonction périodique peut s'écrire comme une somme infinie de sinus et cosinus de fréquences successives :
$f(t)=\sum_{k=0}^{+\infty}a_k\cos(k\omega t) + b_k\sin(k\omega t)$
Ici bien sûr, tu la formule est à prendre pour ton abscisse et ton ordonnée (car tu fais un dessin 2D).
En ne mettant que des cosinus pour l'abscisse et des sinus pour l'ordonnée, on arrive alors à faire ce que tu veux.

Pour faire une TFD, tu peux aller sur ton langage de programmation préféré (par exemple Python), plein de librairies propose de faire ça ! Elles utilisent un algorithme très efficace (la FFT pour Fast Fourier Transform) pour obtenir les coefficients $a_k$ et $b_k$ .
Ca serait inutile de recoder ça par toi-même (mais c'est possible !), cela demanderait beaucoup de temps (déjà bosser un peu sur le sujet) pour moins d'optimalité.

Je te renvoie à plein de vidéos qui traitent de ce sujet :
https://www.youtube.com/watch?v=uazPP0ny3XQ (El Jj, vidéo en français dont tu as visiblement trouvé le lien du blog)
https://www.youtube.com/watch?v=qS4H6PEcCCA (Mathologer, vidéo en anglais)

Tu trouveras en description de ces vidéos pas mal de ressources pour faire ces choses là.