Forum Expresso

Transformées étranges...

Posté par
NervaL928 22-12-14 à 19:03

Bien le bonsoir !
Titre étrange que voici... Quelques explications et illustrations s'imposent !
Je me suis amusé cet après-midi à tracer quelques courbes polaires sur GéoGebra. Plaçons-nous dans un contexte où $0\leqslant\theta\leqslant2\pi$ , ainsi que $0\leqslant t\leqslant2\pi$ .

Soit $r=f(\theta)$ une fonction polaire, et $\left\lbrace\begin{array}{l}x(t)=f(t)cos(t)\\y(t)=f(t)sin(t)\end{array}\right.$ sa paramétration. On place, en fonction de $\lambda$ (le curseur) le point $A(f(\lambda)cos(\lambda);f(\lambda)sin(\lambda))$ . Ensuite, on construit le point $A'$ image du point $A$ par la rotation d'angle $\alpha=f(\lambda)\;radians$ , de sorte que si $S$ est le sommet de l'angle, $AS=A'S$ .
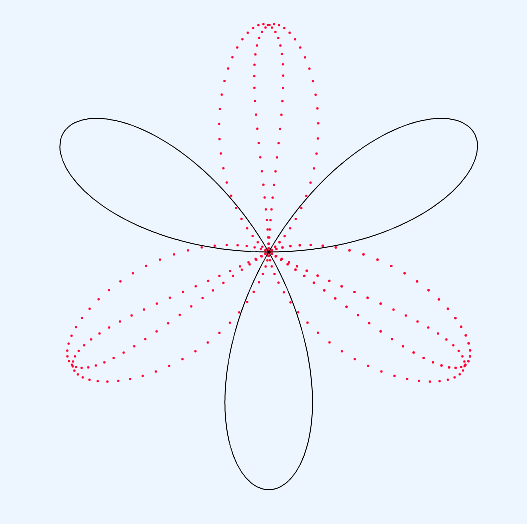
Sur GéoGebra, on active la fonction "suivre la trace" pour le point $A'$ , on choisit "Animer", et on regarde la nouvelle courbe. Essayez, vous verrez, c'est assez amusant !

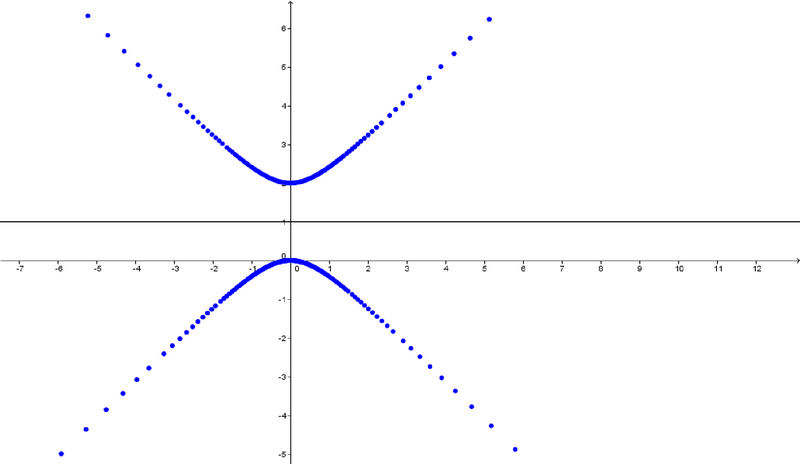
J'ai aussi essayé de faire ça avec des fonction "classiques" (celles du type $y=g(x)$ ), en prenant le point initial $A(\lambda,g(\lambda))$ et en considérant l'angle $\alpha=g(\lambda)\;radians$ . Le résultat est étrange, mais moins beau à voir que certaines courbes polaires (le Papillon de T. Fay rendait plutôt bien).

Une idée de si c'est possible d'obtenir une paramétration de ces nouvelles courbes ? Et quant à prévoir l'allure de cette transformée ?

Sur ce, je vous souhaite de bonnes fêtes à tous !

$En\;noir : r=sin(3\theta)$
$\color{red}{En\;rouge\;:\;la\;transformée}$

Transformées étranges...

Posté par re : Transformées étranges... 23-12-14 à 10:00

Bonjour,

Je ne comprends pas comment est définie f.
si $f(x)=\dfrac{1}{cos x}$
tous les points ont pour abscisse 1. ???

Posté par re : Transformées étranges... 23-12-14 à 16:56

Salut !
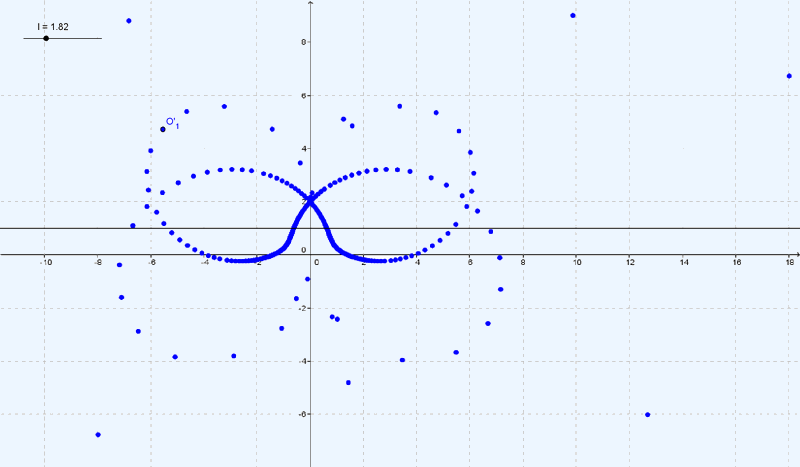
Je trace $r=\frac1{cos(\theta)}$ de paramétration $\left\lbrace\begin{array}{l}x(t)=\frac{sin(t)}{cos(t)}\\y(t)=\frac{cos(t)}{cos(t)}=1\end{array}\right.$ (voir image).
Je place le point $A\left(x(\lambda)=\frac{sin(t)}{cos(t)};y(\lambda)=1\right)$ . Je place $B$ à un endroit quelquonque (je choisis arbitrairement $B(0;0)$ , mais j'aurais pu obtenir une transformée différente selon son affixe). Je place $A'$ tel que $\widehat{ABA'}=\lambda^r$ . Je suis la trace de $A'$ et j'obtiens la courbe en bleu :

Transformées étranges...

Posté par re : Transformées étranges... 23-12-14 à 19:57

Erratum, j'ai pris $\alpha=\lambda^r$ et non pas $\alpha=g(\lambda)^r$ ...
Mais le résultat est un poil plus bizarre en prenant cette seconde valeur de l'angle...
D'ailleurs, j'ai trouvé l'équation de l'hyperbole obtenue, mais il faudrait le démontrer ^^"
$\mathcal{H}:(y-1)^2-x^2=1$
Avec $:\alpha = g(\lambda)^r$ :

Transformées étranges...