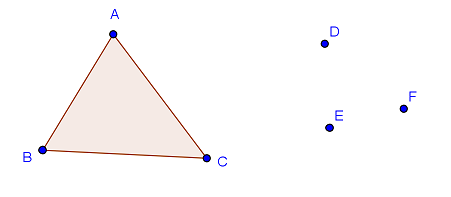
On peut formuler le problème à partir de la figure suivante. Construire à la règle et au compas un triangle A'B'C' égal au triangle ABC tel que D est sur la droite (B'C'), E est sur la droite (A'C'), F est sur la droite (A'B').

Bonjour,

à priori si le triangle DEF est trop "petit",il
semble impossible de respecter ta définition,par contre il est possible de construire un triangle A'B'C' si deux points de DEF sont sur un même coté

Il faut bien un point sur chaque côté mais, en effet, une discussion s'impose sur l'existence d'une solution. Si on considère que DEF est égal à un triangle dont les sommets sont situés à l'intérieur du cercle inscrit au triangle ABC.

OUI

On présume que l'exercice propose des points
qui conviennent....

Bonjour,

se poser la question de construire déja un triangle semblable (mêmes angles) au triangle voulu.

On en trouve une infinité, mais on a des lieux pour chacun des sommets !!
Ensuite il s'agira donc de choisir dans cette infinité un triangle "aux bonnes dimensions" (une seule des 3 suffira, puisqu'ils sont semblables, les deux autres seront alors automatiquement égales)

bonjour,
je m'inspire de mathafou  et je prends les notations de COTLOD

*sur EF on trace un arc capable de l'angle A ( son centre)
*sur DF on trace un arc capable de l'angle B (' son centre)
*il reste à construire une sécante AB  de longueur c passant par F
si K et K' sont les projections de et ' sur cette sécante
KK'=c/2
on construit facilement la projection de ' sur K (intersection du cercle de diamètre ' et du cercle de centre ' de rayon c/2 ,on en déduit K donc AB (sauf étourderie de ma part)

désolée je ne sais toujours pas faire de figure à l'écran

Dans la figure suivante j'ai construit les cercles dans lesquels s'inscrivent les angles égaux aux angles du triangle ABC et j'ai tracé un triangle KLM semblable au triangle ABC. Mais je ne sais pas en déduire le triangle qui sera égal à ABC.

En fait il reste à un résoudre le problème suivant : étant donnés deux cercles sécants, construire une droite passant par un des points d'intersections des deux cercles, qui recoupe chaque cercle aux extrémités d'un segment égal à un segment donné.

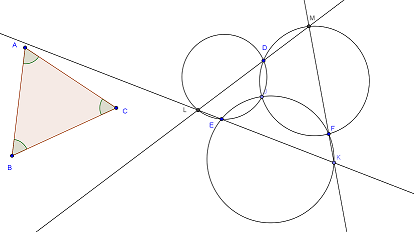
merci à veleda pour la fin du problème. J'écrivais mon post au moment où le votre arrivait. Merci encore à mathafou pour votre contribution.

Voila. Une illustration de cette construction (j'avais pris DE et DF au lieu de DF et EF mais c'est pareil)


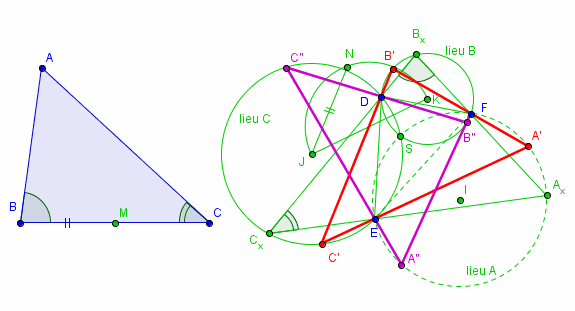
à noter les deux solutions : deux points d'intersections du cercle () et du cercle (; c/2)
ou ce qui revient au même les intersections du demi cercle de diamètre avec (, c/2) et (', c/2) (notations de veleda, JK chez moi)

si on ne précise pas sur quel côté se trouvent D, E, F on obtient d'autres solutions par permutations.
on peut aussi tracer les arcs capables dans l'autre sens ce qui donne encore d'autres solutions (angles de droites à pi près), avec retournement de ABC éventuellement.

On remarquera que si on trace les arcs capables des trois angles A, B, C, ils se coupent en un même point S qui est le centre de similitude de tous les triangles semblables A_xB_xC_x
Le plus grand de ces triangles semblables est obtenu avec BC // JK (sur mes notations)
Le triangle IJK est semblable à ABC (I centre de l'arc capable de A).
On peut trouver des triangles semblables entre eux un peu partout dans cette figure (S centre de similitude !) et rattacher cela au problème inverse : inscrire DEF dans ABC. On trouve alors de même un centre de similitude (point de Miquel) pour tous les triangles DEF semblables inscrits dans ABC, et de même on obtient le plus petit triangle DEF comme étant le triangle podaire de ce centre de similitude.
Un thème plein de richesses donc...

Pour préciser le détail de la construction finale de BC = donnée, on rattache cela au problème de la "double corde" :

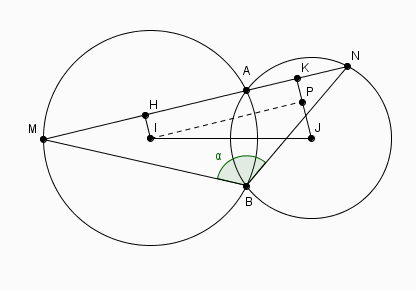
étant donnés deux cercles se coupant en A et B et une sécante variable MAN
la propriété qui nous sert ici est IP = HK = MN/2

il y a d'autres propriétés intéressantes de cette figure, notamment que l'angle MBN est constant ...
(c'est lié à la similitude de centre S évoquée précédemment)

>>mathafou
merci pour la figure
si D,E,F sont alignés c'est la droite de Menelaüs du triangle donc..?

c'est fort possible que cette droite là porte un nom. mais je ne connais pas. (Théorème de Menelaüs pour une sécante = CNS pour que 3 points soient alignés, oui, mais pas de "droite de Menelaüs" dans mes tablettes, on parle peut-être de la même chose : une droite pour le théorème de Menelaüs)
en tout cas la construction marche aussi si D, E, F donnés sont alignés.