Inscription / Connexion Nouveau Sujet
triangle dans hyperbole
Bonjour à tous
inspiré par l'un des sujet d'exercice les plus longs de l'ile (118 réponses pour l'instant et l'exo n'est toujours pas terminé)
on cherche les triangles équilatéraux inscrits dans (c'est à dire avec leurs sommets sur) une hyperbole équilatère
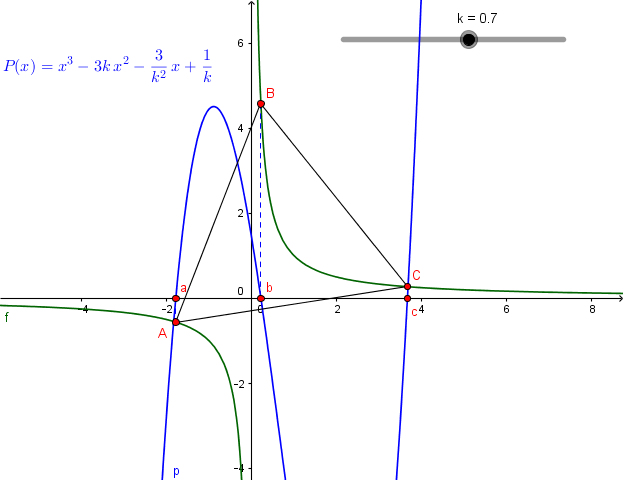
soit donc l'hyperbole y = 1/x bien connue
et on cherche des triangles ABC "inscrits" dans cette hyperbole
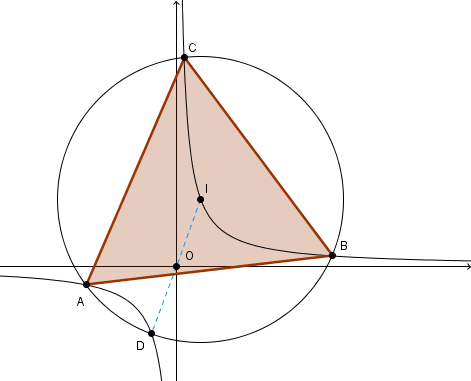
dans la figure ci dessus je suis parti du point I (à priori n'importe où sur l'hyperbole)
soit D le symétrique de I par rapport à l'origine O (= le centre de l'hyperbole)
le cercle de centre I et de rayon ID recoupe l'hyperbole en trois autres points A, B, C qui forment un triangle équilatéral
l'exo précité était dans le cas particulier où I = (1; 1) et alors le point D est confondu avec A (le cercle est tangent à l'hyperbole en A)
et l'exercice avait pour but de démontrer dans ce cas particulier que ABC est bien équilatéral. ce qui dans ce cas particulier est bien du niveau lycée. contrairement au cas général.
la figure précédente est obtenue en demandant gentiment à Geogebra les intersections du cercle et de l'hyperbole
malheureusement Geogebra n'est pas toujours d'accord et refuse parfois de façon purement caractérielle de calculer les points d'intersection si on déplace I !
le but de l'énigme est de construire "à la règle et au compas" un tel triangle équilatéral
donc sans besoin de faire résoudre par Geogebra l'équation du 4ème degré (hé hé) qui ne lui plait pas tant que ça.
"chacun sait" que les équations générales du 4ème degré ne sont pas résolubles à la règle et au compas !
alors ???
la solution vient de ne pas partir d'un point I défini et avec la construction précédente, mais d'un autre paramètre que I pour construire "un" triangle inscrit.
et construction qui doit fonctionner quel que soit la "valeur" de ce paramètre (point déplaçable quelque part, mesure d'un segment, valeur d'un angle etc) en en faisant varier à volonté ce paramètre ainsi engendrer "sans disparition inopinée" tous les triangles équilatéraux inscrits dans cette hyperbole.
bien entendu cet exercice là peut amener "assez loin" ne serait ce que de justifier la propriété générale énoncée au début : que quel que soit le point I choisi, le triangle obtenu est toujours équilatéral
et d'autres propriétés reliant triangles équilatéraux et hyperboles "circonscrites" (si ABC est inscrit dans l'hyperbole, c'est la même chose de dire que l'hyperbole est circonscrite au triangle)
en dehors de demande de précisions, merci de blanquer vos pistes, idées, démonstrations etc...
Oui on peut faire ça par des calculs explicites.
ou en considérant que toute hyperbole équilatère qui passe par les sommets d'un triangle quelconque passe forcément par son orthocentre et vice versa
(que toute conique qui passe par les sommets d'un triangle quelconque et son orthocentre est une hyperbole équilatère, éventuellement dégénérée en paire de droites perpendiculaires)
mais "l'exo" n'est pas vraiment là mais sur la construction à la règle et au compas d'un tel triangle variable pour pallier aux déficiences de geogebra qui refuse parfois de tracer dynamiquement l'intersection pourtant visible d'un cercle variable avec une hyperbole fixe...
(pas de problème en statique, avec une figure fixe il veut bien mais dès qu'on déplace I les points deviennent "non définis" puis réapparaissent si on continue à déplacer I)
ceci dit démontrer les propriétés de cette figure hyperbole + triangle équilatéral est un pas possible vers la solution bien sûr,
mais relier une construction avec des calculs sur les affixes ... bof ça va pas être évident.
il faut repartir plus vers de la géométrise "synthétique" ou "déductive" selon comment on appelle ça (datant des grecs et de ce qui a été prouvé en plus depuis, par exemple cercle d'Euler etc)
Luzak : l'absence de blank est ici peu grave vu que ça ne spolie pas l'exercice proprement dit (construire etc ...)
Bonjour
Celle là elle va faire mal...
J'oublie la règle et le compas...
Pour respecter les données pout un triangle ABC
Nous devons avoir A(xa,ya) B(xb,yb) C(xc,yc)
avec xa=1/ya xb=1/yb et xc=1/yc
et K= ( xa-xb)² +(ya-yb)²=
( xa-xb)² +(ya-yb)²= (xa-xc)²+(ya+yc)²=
(xa-xc)²+(ya+yc)²= (xb-xc)²+(yb-yc)²
(xb-xc)²+(yb-yc)²
La suite pour les bons....
ces calculs seront inextricables
au moins écrire K² comme égalités !! ça va déja virer les racines carrées !
(mais foin de calculs ici)
le problème :
si on part d'un point lié à l'hyperbole (le centre du triangle ou un des sommets) une équation du troisième ou 4ème degré est incontournable, donc insoluble à la règle et au compas
solution :
il faut partir dans l'autre sens : tracer un triangle quelconque et construire l'hyperbole (une)
la figure obtenue sera à une similitude près la figure désirée
et on sait faire une similitude à la règle et au compas ...
il faut donc savoir tracer (= construire ses asymptotes et son centre) une hyperbole "courante" circonscrite à un triangle A'B'C' donné (ici équilatéral), en choisissant un paramètre "judicieux" pour le choix de cette hyperbole
(il existe une infinité d'hyperboles équilatères circonscrite à un triangle donné : le faisceau de coniques défini par les sommets et l'orthocentre du triangle)
pour la définir, on peut choisir un tas de paramètres plus ou moins commodes : un 5ème point, la direction de ses asymptotes, la position de son centre (qui d'après un théorème bien connu sur les faisceaux de coniques est lui même sur une certaine conique qui est ... un truc déja cité dans la discussion)
reste à savoir quel paramètre sera le plus judicieux pour faciliter la construction et pour faciliter la similitude finale.
Trois sommets du triangle, deux points à l'infini dans des directions orthogonales pour avoir une hyperbole équilatère : 5 points déterminent une conique et permettent de faire toutes les constructions voulues à la règle et au compas.
tout à fait
mais c'est un peu bourrin de faire ça.
la seule chose qu'on peut dire ainsi c'est que "c'est possible".
(et si on s'arrête là, les constructions vont être "assez compliquées" si on ne cherche pas à creuser d'avantage)
la seule chose qu'on peut dire ainsi c'est que "c'est possible".
Oui, c'est possible, et même faisable. On se donne
Grâce à notre ami Pascal, on construit les symétriques
Soit
Soient
Soit
Soit
Quand on a
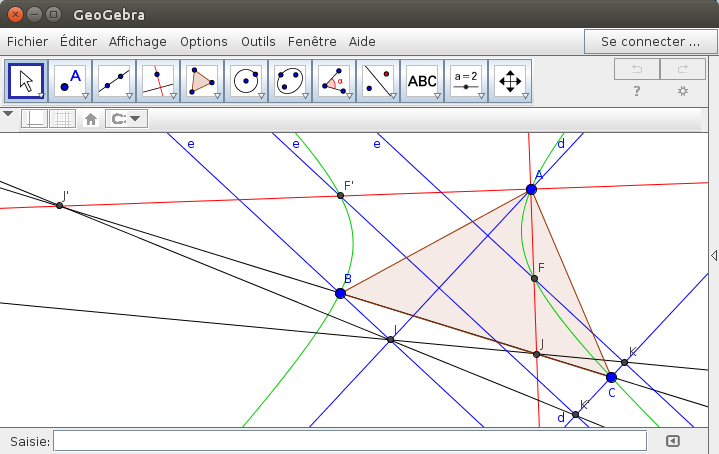
Pour faire avancer,
Une observation:
Si on prend un point aussi particulier qu'un sommet de l'hyperbole 1/x
par exemple A(-1,-1) on trouve B(2+ 3,
3,)
et C(,2+
 3)
3)
Ces valeurs particulières peuvent donner une piste....
Oui, c'est effectivement pas si compliqué si on pense à construire le symétrique de A par rapport aux axes (c'est à dire par Pascal les points de la conique qui sont sur une droite passant par A et parallèle à l'autre axe)
on obtient alors le centre en deux coups de cuillère à pot.
encore fallait-il y penser 
reste la suite ...
à dpi,
le cas particulier en est effectivement un (c'est déja dit :
l'exo précité (
et l'exercice avait pour but de démontrer dans ce cas particulier que ABC est bien équilatéral. ce qui dans ce cas particulier est bien du niveau lycée. contrairement au cas général.
malheureusement le cas général ne se laisse pas "résoudre" si facilement, d'où ce sujet ci.
suite des particularités:
Le coté de ce triangle mesure 2 2
2 3
3
le centre du cercle circonscrit est le sommet de l'autre hyperbole.
Bonjour,
Mathafou a écrit :
sans besoin de faire résoudre par Geogebra l'équation du 4ème degré (hé hé) qui ne lui plait pas tant que ça.
Il semble que Il semble que Geogebra résolve mal les équation de degré 4 ou 3 dont le coefficient du terme de plus haut degré soit lui-même une puissance d'un paramètre.
Sans doute un dépassement de capacité non-traité... car lake fournit (18-02-16 à 17:23) un P(x) dont ce coefficient est ramené à 1 et qui fonctionne parfaitement....
A confirmer.
dpi :
dans cet exemple de "cas particulier résoluble"
le centre du cercle circonscrit est le sommet de l'autre hyperbole.
vu que c'est comme ça qu'a été défini le triangle : par des points d'intersection de ce cercle avec l'hyperbole !!
tu veux dire l'autre sommet de la même hyperbole ? (A est l'un des sommets et I l'autre, tout à fait, vu que c'est aussi comme ça qu'ils ont été définis, I (1; 1) étant un sommet et A le symétrique par rapport au centre est donc l'autre sommet)
Suite
Je n'étais pas dans la figure de départ mais..
si on dit que i est au sommet de l'hyperbole "positive" (1,1) notre triangle
particulier à A sur le sommet de la négative (-1,-1) tangent et B et C sur l'hyperbole
positive avec les coordonnées données auparavant...
ah d'accord tu parlais de l'autre branche d'hyperbole
(l'hyperbole est l'ensemble de la courbe, la réunion de deux branches d'hyperbole)
pas d'une autre hyperbole, car il n'y en a qu'une seule, avec deux branches
question de vocabulaire.
c'est pour cela que j'ai mis positive "entre" ,ok...
Le lieu géométrique des centres me semble "curieusement"
sur l'hyperbole ....
oui c'est ce que j'ai dit quasiment tout au début
l'orthocentre de tous les triangles équilatéraux ou pas inscrits est toujours sur l'hyperbole (quand elle est équilatère, c'est à dire avec ses asymptotes à angle droit)
et pour un triangle équilatéral, l'orthocentre est le "centre" tout simplement
pratiquement tous les "centres" (points remarquables) d'un triangle) équilatéral sont en ce même point, y compris l'orthocentre donc, ou indéterminés.
noter toutefois que c'est ici une donnée de l'énoncé, vu qu'on part de ce centre pour construire le triangle !!

 Cliquez pour afficher
Cliquez pour afficher