triangle rectangle

 Niveau autrePartager :
			        
triangle rectangle
Posté par 
C4amille  24-03-11 à 21:33
bonsoir

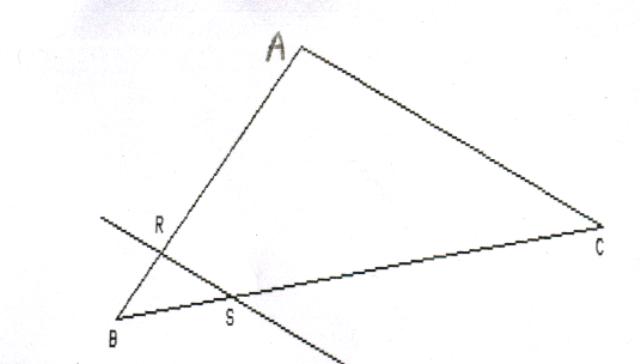
sur la figure ci contre qui n'est pas en vraie grandeur on a:

BR= 2,7 cm 

BS= 4,5 cm

BC= 22 cm

AC= 17,6 cm

les droites (RS) et (AC) sont parallèles.

1.a)Prouver par le calcul que RS = 3,6 cm.

  b) Calculer BA.

2.a) Démontrer que le triangle BRS est un triangle rectangle.

Préciser son angle droit. 

  b) En déduire que les droites (AB) et (AC) sont perpendiculaires.

mes reponses:

1.a) dans le triangle BRS rectangle en R on a l'égalité de pythagore

BR²= RS²+BS²

2,7²=RS²+4,5²

7,29=RS²+20,25

RS²= 7,29-20,25

RS²= -12,96

RS= -12,96

RS= 3,6 cm

b) calculer BA

dans le triangle BAC rectangle en A on a l 'égalité de pythagore

BA²= AC²+CB²

BA²= 17,6²+22²

BA²= 309,72+489

BA²= 798,72

BA= 798,72

BA= 28,3cm

la droite BA mesure 28,3 cm.

2) a)???

   b) les droites (AB) et (AC) sont perpendiculaire car le triangle ABC est rectangle en A

besoin d aide pour la question a) du 2) et me dire si ce que  j ai fait et correct

 Posté par 
plvmptre : triangle rectangle  24-03-11 à 21:45
re,

rien ne dit que BRS est rectangle

thales

BR/BA = BS/BC = RS/AC

2,7/BA = 4,5/22 = RS/17,6

produit en croix :

(4,5*17,6) = (22*RS)

79,20 = 22RS

RS = 79,20/22 = 3,6
 Posté par 
plvmptre : triangle rectangle  24-03-11 à 21:46
calculer BA :

BR/BA = BS/BC = RS/AC

2,7/BA = 4,5/22

(2,7*22) = BA*4,5

59,4 = BA*4,5

BA = 59,4/4,5 = 13,2
 Posté par 
plvmptre : triangle rectangle  24-03-11 à 21:49
2.a) Démontrer que le triangle BRS est un triangle rectangle.

Préciser son angle droit. 

ici pythagore : si le carré du + grand cote est = à la somme des ² des 2 autres cotes, alors le triangle est rectangle

BS² = BR²+RS²

4,5² = 2,7²+3,6²

20,25 = 7,29+12,96

BRS rectangle en  R
 Posté par 
plvmptre : triangle rectangle  24-03-11 à 21:55
2) demontre que BAC est rectangle en A 

BRS rectangle en R

BAC rectangle en A

RSAC
 Posté par 
plvmptre : triangle rectangle  24-03-11 à 21:57
errreur 

ABAC

ne tient pas compte de ce que j'ai ecrit a 21h55, je me suis embrouillé, demontre juste que BAC rectangle en A
 Posté par 
C4amilletriangle rectangle  24-03-11 à 22:00
est ce que la question 2. b) est bonne 
 Posté par 
plvmptre : triangle rectangle  24-03-11 à 22:01
demontre juste que BAC rectangle en A, tu l'as dit mais faut le prouver 
 Posté par 
C4amilletriangle rectangle  24-03-11 à 22:02
je m embrouille les pinceaux aussi pour la derniere question 2.b)
 Posté par 
plvmptre : triangle rectangle  24-03-11 à 22:05
si le carré du + grand cote est = à la somme des ² des 2 autres cotes, alors le triangle est rectangle

BC² = AB²+AC²

22² = 13,20²+17,6

484 = 174,24+309,76

BAC rec en A
 Posté par 
plvmptre : triangle rectangle  24-03-11 à 22:09
je te remets tt l'exo :

rien ne dit que BRS est rectangle

thales

BR/BA = BS/BC = RS/AC

2,7/BA = 4,5/22 = RS/17,6

produit en croix :

(4,5*17,6) = (22*RS)

79,20 = 22RS

RS = 79,20/22 = 3,6

calculer BA :

BR/BA = BS/BC = RS/AC

2,7/BA = 4,5/22

(2,7*22) = BA*4,5

59,4 = BA*4,5

BA = 59,4/4,5 = 13,2

2b)si le carré du + grand cote est = à la somme des ² des 2 autres cotes, alors le triangle est rectangle

BC² = AB²+AC²

22² = 13,20²+17,6

484 = 174,24+309,76

BAC rec en A

ACAB
  Posté par 
C4amilletriangle rectangle  24-03-11 à 22:11
merci de m avoir aider