Inscription / Connexion Nouveau Sujet
triangle rectangle et parabole
Bonjour,
encore un petit problème de construction géométrique (à mon avis pas si facile)
on donne une parabole définie par son foyer F et sa directrice 
(ou pourra sans perte de généralité utiliser la parabole d'équation y = x² avec F = (0; 1/4) et  : y = -1/4)
: y = -1/4)
et un point A quelconque de son axe (idem, A (0; m))
construire (à la règle et au compas bien sûr) les triangles rectangle isocèle ABC, rectangles en A et avec B et C sur la parabole.
(il y en a 4 : 2 sont triviaux, mais les deux autres ... moins)
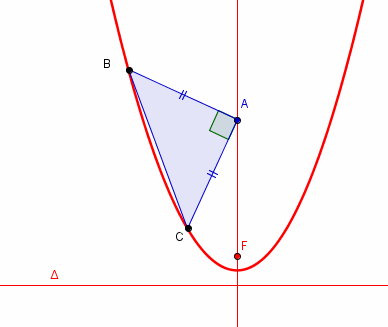
pour ne pas allourdir la construction on ne détaillera pas la construction des points d'intersection d'une droite quelconque avec la parabole (c'est facile mais inutilement long, le problème n'est pas là)
Par contre on rappelle qu'il est impossible de construire en général les intersections d'un cercle quelconque avec une parabole, ou de deux paraboles quelconques etc (pour cause d'équation générale de degré 4)
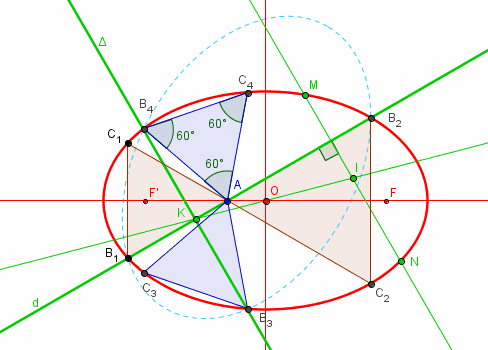
(la figure ci dessus a été construite avec ma construction et pas "ajustée jusqu'à ce que")
bonjour mathafou,
j'ai bien trouvé les deux constructions triviales mais pas les deux autres
merci pour cet exercice
Bonjour veleda,
merci de t'intéresser à ce petit problème.
il y a deux approches, l'une algébrique va avoir pour but de dégager des propriétés géométriques intéressantes, ou au pire d'obtenir une certaine équation du second degré qu'on va "construire de force" (méthode générale de résolution géométrique des équations du second degré), en partant de l'équation de la parabole etc ...
Au fait comment à partir d'une équation de degré 4 voire plus obtient-on une simple équation du second degré ? en utilisant (factorisant par) la solution triviale.
c'est l'existence de cette solution triviale qui rend la construction possible (en plaçant A n'importe où dans le plan la construction règle et compas serait impossible)
il va de soi que ce n'est pas ma façon de faire préférée 
l'autre méthode purement géométrique nécessite bien entendu des connaissances sur les propriétés géométriques des paraboles 
et le détour par des choses qui normallement ne seraient pas constructibles (intersection de deux paraboles par exemple) mais qui à cause de cette fameuse solution triviale le sont.

 Cliquez pour afficher
Cliquez pour afficher
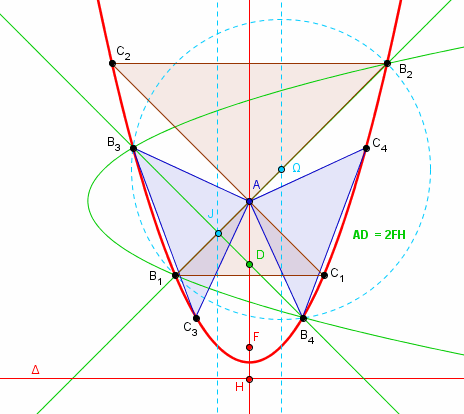
 /2, celle qui transforme les points Ci en points Bi, d'où les points cherchés sont les intersections de ces deux paraboles.
/2, celle qui transforme les points Ci en points Bi, d'où les points cherchés sont les intersections de ces deux paraboles.
 C3 et de la rotation de -
C3 et de la rotation de -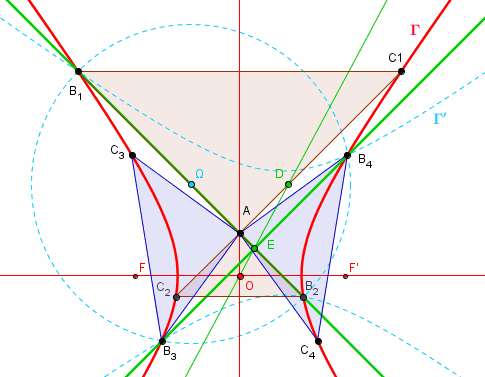
 de B1B2
de B1B2