- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
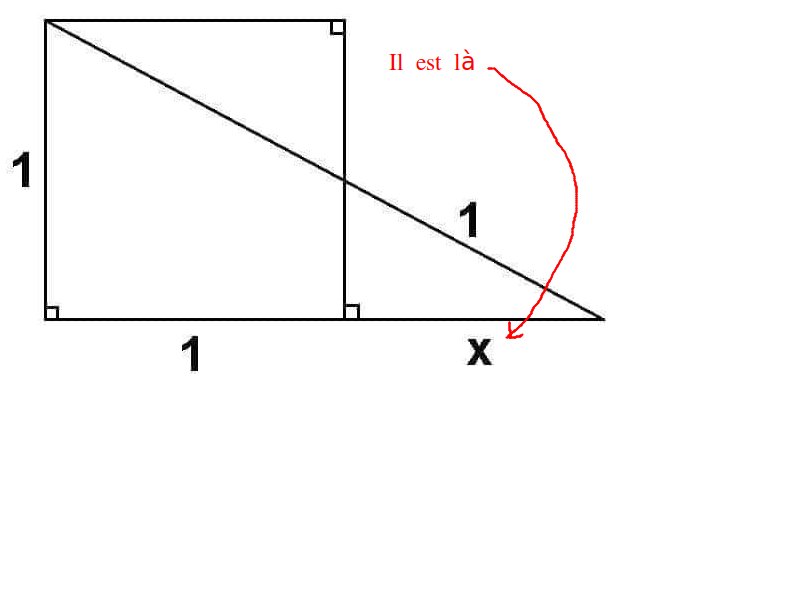
trouver x
j'ai essaye d utiliser pythagore et thales mais rien ne marche svp comment trouver x
Bonjour
et pourtant si, ça marche
le th de Pythagore dans le petit triangle pour avoir en fonction de x la hauteur du petit triangle, puis le th De Thalès pour écrire que x / (x+1) est égal à cette hauteur (sur 1)
et après il faudra résoudre l'équation obtenue
Bonjour,
c'est certain que avant de résoudre une équation, encore faudrait il déja l'écrire !! (ici)
ensuite on verra comment faire pour résoudre une telle équation...
(elle se factorise dans ... mais on n'est que en terminale ...)
Tu sembles assez coutumier du fait de ne rien écrire du tout de ce que tu prétends avoir essayé ...
espérant (tu as tort) recevoir des calculs tout faits ici ...
nota :
il serait bien plus facile, tout calculs faits, de choisir comme inconnue u = AE plutôt que x = BE
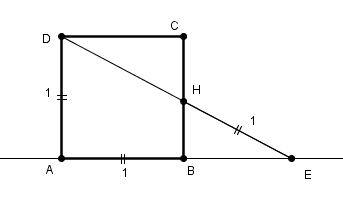
mais bon ça ne change apparemment pas grand chose vu que x = u-1, quoique ...
l'équation en u se résout par des méthodes éprouvées en passant par une succession d'équations du second degré
celle en x est plus compliquée. en fait elle se résout en commençant par poser x = u-1 !!
on peut chercher dans une telle direction ... et s'essouffler à vouloir trouver absolument une preuve "géométrique" directe de ça ...
ou bien retrousser ses manches et suivre les pistes calculatoires déja indiquées (c'est facile si on suit la piste indiquée de prendre AE comme inconnue plutot que x de l'énoncé)
il faut savoir au bout d'un certain temps de recherches infructueuses décider de méthodes "de bourrin" au lieu de s'épuiser vainement à chercher des trucs qu'on ne voit pas 
(on retrouvera en quelques lignes seulement de calculs le ou un
selon la variable choisie)
une idée possible pour la géométrie pure : connaitre les propriétés géométriques des conchoïdes ...  bof ...
bof ...
mehdi000 reste muet
il attend peut être qu'on lui écrive des formules à sa place, ne serait ce que les Thalès et Pythagore par lesquels tout commence ... et toujours pas écrites ici !!
(avant de chercher à résoudre il faut de toute façon écrire déja les équations ... bis répétita)
dommage que le demandeur se fiche ainsi du monde en ne participant pas activement à la discussion ...
on attend toujours qu'il écrive l'équation comme déja dit et répété.
ensuite seulement on pourra penser à la résoudre ...
mais c'est peine perdue, il ne fera rien du tout. il attend qu'on le fasse à sa place ! il pourra attendre longtemps !
peut être donnerai-je ma solution et autres "annexes" géométriques à la rentrée en septembre pour les autres personnes intéressées...
Ce qui me sidère le plus, c'est que le demandeur pose son post en espérant la réponse toute faite....
Il a sa réponse, il est content, pas de réponse, eh ben il va aller voir ailleurs sur un autre forum !!
Cela ne fera pas plus progresser le demandeur...
ça me fait penser à cette pub du CIC qu'on entend actuellement et qui offre une certaine somme d'argent suivant la mention obtenue au bac et qui dit en gros (au deuxième degré) : si vous êtes con ne vous attendez pas à recevoir de l'argent ...
je crois bien que l'une d'entre elles (contexte mathématique) dit que x se trouve ... entre w et y !!!