Inscription / Connexion Nouveau Sujet
Trouver position d'une point en respectant une distance
Bonjour,
J'ai deux points dans l'espace 3d (node1,node2) comme montre l'image
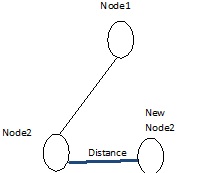
je veux déplacer le point node2 par une distance ("distance")mais tout en respectant que la distance entre node1,node2 reste la même comme node1, new node2 position
J'ai essayé de faire ça
où
node1(x1,y1,z1)
node2(x2,y2,z2)
j'ai tout simplement dit que la nouvelle position de node2 elle va être (x2+distance,y2,z2)
mais lorsque j'ai fait mes essaies j'ai trouvé que la distance entre la nouvelle posiiton de node2 et node1 est changé et ce n'est pas ce que veut
je sais qu'il me manque une chose mais je n'ai pas pu la trouvé , je pense que je dois calculer une angle aussi mais c'est l'angle de quoi ? et comment je vais la calculer
salut
pour conserver la même distance il faut que node2 reste sur la sphère de centre node1 et de rayon nodenode2initial ...
tu veux dire ça:
je centre un cercle sur noeud 2 de rayon d, je centres un autre cercle sur noeud 1 de rayon distance noeud1-noeud2, et je cherches l'intersection entre les deux cercles. Normalement, il y en a deux, donc je prends la bonne!
j'ai essayer de faire ça mais ,j'ai échoué
lorsque j'ai cherché sur le net comment faite l'intersection cercle-cercle j'ai trouvé qu'ils ont utilise pour le centre que x,y mais dans mon cas j'ai des coordonnées 3D
lorsque j'ai cherché dans le net comment faire l'intersection sphere/sphere j'ai trouvé que le résultat c'est une cercle et n'ai pas une point dont dans mon cas je cherche qu'une points qui sera la nouvelle position de node2
non ce n'est pas ce que j'ai dit ....
en plus il serait bien d'extraire l'essentiel plutôt que d'utiliser des notations "à la mord moi l'nœud" ....
on veut déplacer un point M d'une distance d tout en restant à la même distance du point P ....
donc PM est constante ... donc M est sur la sphère de centre P et de rayon PM oùM est à sa position initiale ....
donc PM est constante
OUi, exactement
donc M est sur la sphère de centre P et de rayon PM oùM est à sa position initiale
Ok, mais comment puis je faire ça ?
tu as les coordonnées de P et de M1 (position initiale de M) donc tu as l'équation de la sphère
on pose r = PM1 (rayon de la sphère)
ensuite effectivement tu veux M2 sur la sphère et à la distance d de M1
donc il se trouve aussi sur la sphère de centre M1 et de rayon d
donc tu cherches un point N ( = M2) tel que NP = r et NM1 = d
il en existe une infinité ...
tu peux essayer par tâtonnement .... en fixant une coordonnée par exemple ...
tu as deux équations et trois inconnues :: tu peux donc fixer une coordonnée (et pas n'importe comment non plus puisqu'elle doit être "voisine" des coordonnées de P ou de M1 en relation avec les rayons) puis déterminer les deux autres coordonnées à partir des deux équations ....
Désolé mais je n'ai pas encore compris comment choisir ce coordonnés et qu'est ce que voulez vous dire par voisine ?
En faite je ne suis pas mathématicienne et mon problème est posé comme une étape d'un autre projet c'est pour ça je pose beaucoup de questions
l'équation de sphere est
(x-a)+(y-b)[sup](z-c)[/sup]=r
pou que je trouve des coordinnée voisine est ce que je met comme ça
(x-a)+(y-b)[sup](z-c)[/sup]=r
(x1-a)+(y-b)[sup](z1-c)[/sup]=r
?
Désolé , j'ai posté la réponse avec le compte de mon amie
En faite je ne suis pas mathématicienne et mon problème est posé comme une étape d'un autre projet c'est pour ça je pose beaucoup de questions
l'équation de sphere est
(x-a)2+(y-b)2+(z-c)2=r2
pou que je trouve des coordinnée voisine est ce que je met comme ça
x-a)2+(y-b)2+(z-c)2=r2
x1-a)2+(y1-b)2+(z-c)2=r2
notons (a, b, c) les coordonnées de P et (u, v, w les coordonnées du point M1 initial
on a donc
(x - a)2 + (y - b)2 + (z - c)2 = r2
(x - u)2 + (y - v)2 + (z - w)2 = d2
on peut donc donner une valeur à z et chercher x et y ...
et vu que tu as une somme de carrés = r2 ou d2 tu vois bien que z - c ou z - w ne peut être trop grand .... sinon tu dépasses le rayon ...
merci bien
c'est juste pour résumer
je fait ça
x - a)2 + (y - b)2 + (z - c)2 = r2
(x - u)2 + (y - v)2 + (z - w)2 = d2
ensuite je fixe z comme ça
|z - c| =< r et |z - w| =< d
ça va me donné
|2z-c-w|=<r+d
je trouve une valeur de z (je vai travailler par une fonction que me donne une valeur aléatoire
je met la valeur de z obtenue dans les deux equation je vais trouvé x,y,z
ce sont les coordonnée de point désirer
pourtant que ça fait longtemps que je n'ai pas essayer de résoudre une équation mathématique j'ai essayer de résoudre les deux équations comme suite
j'ai premièrement développé les formes avec parenthèses
x2-2ax+a2+y2-2by+b2=
x2-2ux+u2+y2-2vy+v2=
ou  =r2-(z-c)2
=r2-(z-c)2
 ==d2-(z-w)2
==d2-(z-w)2
Soustraction membre à membre :
-2ax+a2-+b2+2ux-u2+2vy-v2= -
-
maintenant est ce que qu'il y a en math une méthode rapide pour résoudre cette nouvelle equation sion je pense de trouvé la valeur de x par rapport à y ensuite je deplace x par ce nouvelle valeur dans une équation des deux premier équation je trouvé une valeur de y
et je vais trouvé par remplacement le valeur de x mais c'est une long étape
développer n'est peut-être pas le plus judicieux ....
après avoir choisi aléatoirement z
on a alors
(x - a)2 + (y - b)2 = e (1)
(x - u)2 + (y - v)2 = f (2)
avec e et f positifs
par soustraction on a
(u - a)(2x - a - u) + (v - b)(2y - b - v) = e - f
il est alors aisé d'exprimer x ou y en fonction de l'autre et de remplacer dans l'une ou l'autre des équations (1) ou (2)
.....
Re
j'étais entrain de tester la solution mais j'ai tombé dans un problème
premièrement pour calculer z j'ai utiliser random qui me donne un valeur aléatoire entre deux bornes
z=RangeRandom(0.5*(w+c-r-d),0.5*(r+d+c+w));
e=sqrt(pow(r,2)-pow((z-c),2));
f=sqrt(pow(d,2)-pow((z-w),2));
et hop j'ai arrêtez ici parce que
je pense que je dois limiter z plus que ça parce que des fois random me donne un valeur de z
grand, et lorsque je calcule f "pow(d,2)-pow((z-w),2)" il me donne un valeur négatif ce qui rend impossible de calculer sqrt


