Inscription / Connexion Nouveau Sujet
Un ensemble de points...
Soit S un ensemble de n points distincts du plan tel que la distance entre deux points de S soit toujours au moins 1. Quel est le nombre maximal de paires d'éléments de S qui peuvent se trouver à distance exactement 1 ?
Cliquez pour afficher
Bonjour à tous évidemment. 
Bonsoir,
je ne suis pas certain de bien comprendre le problème.
Pour donner un exemple, pour 8 points, je trouve un maximum de 14 paires.
Est-ce la réponse attendue ?
salut
je ne comprends pas trop non plus ....
Soit S un ensemble de n points distincts du plan tel que la distance entre deux points de S soit toujours au moins 1
si je prends n points alignés d'ordonnées nulle et d'abscisse paire .....
la distance entre deux points distincts de S est toujours au moins 2 .....
Il faut trouver une borne supérieure sur le nombre de paires de points à distance exactement 1, c-à-d qu'il est impossible d'en avoir plus sans violer la condition que tous les points soient à distance au moins 1.
Par exemple si j'ai 4 points, je peux les disposer en carré de côté 1 et alors j'ai 4 paires de points à distance 1. Mais je peux aussi les disposer en parallélogramme avec la petite diagonale qui vaut 1, et là j'en ai 5.
Le but est de trouver la borne supérieure pour n quelconque.
si on a une position "maximale" pour n points au sens qu'elle conduit au maximum de paires avec n points alors l'ajout d'un point ne peut conduire à strictement plus de trois paires en plus
3(n-2) semble un bon majorant pour n > 2....
Oui, la réponse "attendue" était 3n: on constuit un graphe avec les n ponts comme sommets et une arête entre deux moints si et seulement si ils sont à distance 1. Chaque sommet est de degré au maximum 6 (il est relié au maximum à 6 autres points), et la somme des degrés de tous les sommets est égale au double du nombre d'arêtes. Mais évidemment, sauf à considérer n infini, les sommets "au bord" du graphe seront reliés à moins de 6 autres sommets, donc c'est toujours un peu moins.
oui j'avais vu pour 3n et j'ai mis 3(n - 2) à cause des pb de "bords" ....
on remarquera qu'avec ma formule le majorant est le maximum lorsque n = 3 ....
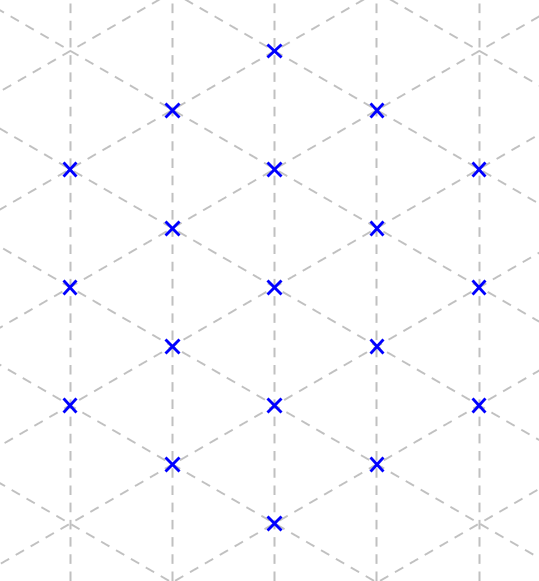
Pour trouver un majorant on peut penser que le maximum est atteint quand on a un hexagone complet.
Si c'est bien le cas le nombre de paires à distance 1 pour n points est inférieur ou égal à
Et ce majorant est atteint une infinité de fois.
En regardant des petites valeurs de n, je me demande si le nombre maximum de paires(1) pour n points n'est pas la partie entière du majorant.
Si quelqu'un veut se lancer dans une démonstration...
Annuler
connectez vous