Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Niveau exercices
Un sacré équivalent !
Posté par gui_tou
Bonjour à tous,
Je vous propose un exercice de mon TD, tel quel (bon c'est quand même une exo de l'ENS, donc il est brut  )
)
Citation :
Soit un réel strictement positif. On considère la fonction
un réel strictement positif. On considère la fonction =\Bigsum_{k=1}^n{4$\fr{1}{x-k) définie sur
définie sur ![3$]n,+\infty[](https://latex.ilemaths.net/ile_tex.cgi?3$]n,+\infty[) .
.
On appelle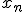 le réel supérieur à
le réel supérieur à 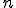 tel que
tel que =a) .
.
Donner un équivalent de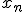 .
.
Soit
On appelle
Donner un équivalent de
Comme il n'est vraiment pas fastoche, je donne quelques pistes (à lire dans l'ordre)
Piste 1
 Cliquez pour afficher
Cliquez pour afficherPiste 2
 Cliquez pour afficher
Cliquez pour afficherPiste 3
 Cliquez pour afficher
Cliquez pour afficherVoilà, bonne réflexion

Bonjour gui_tou,
C'est un exercice "classique" intéressant qui se résout très simplement si on pense à:
 Cliquez pour afficher
Cliquez pour afficheron prend et on pose
en suite on pose
et on en deduit que
.

(a ete demontré sur ce site:

) et

(f'=-f^2) ;on a lors
.
Bonjour Elhor,
La démonstration que je propose n'est pas très éloignée de la tienne:
 Cliquez pour afficher
Cliquez pour afficher

 sauf erreur bien entendu
sauf erreur bien entendu

