Inscription / Connexion Nouveau Sujet
Une drôle de monnaie dans une drôle de contrée
Bonjour,
Désolé pour l'avance à l'allumage, des impératifs de dernière minute. Mille excuses ! 
Dans cette contrée lointaine on ne dispose pas de pièces de monnaie ni de billets, uniquement de « coupures » de 84 centimes, 132 centimes, 231 centimes et 308 centimes d'euros, mais en quantité infinie.
Alors évidemment les habitants ne peuvent pas faire l'appoint pour certaines sommes, comme 85 centimes par exemple, mais bon ça ne semble pas les déranger plus que ça.
En revanche ils affirment qu'à partir d'une certaine somme ils peuvent tout payer très exactement.
- Quelle est la plus grande somme d'argent S exprimée en centimes d'euro qu'ils ne peuvent pas payer exactement ?
- Comment payer exactement S+1 ? Même question pour S+2, S+3, S+4 et S+5.
bonjour
la plus grande somme non payable exactement: 2017
ensuite:
84* 7 + 132* 5 + 231* 2 + 308* 1 = 2018
84* 4 + 132* 4 + 231* 1 + 308* 3 = 2019
84* 4 + 132* 4 + 231* 5 + 308* 0 = 2019
84* 4 + 132* 11 + 231* 1 + 308* 0 = 2019
84* 15 + 132* 4 + 231* 1 + 308* 0 = 2019
84* 1 + 132* 3 + 231* 0 + 308* 5 = 2020
84* 1 + 132* 3 + 231* 4 + 308* 2 = 2020
84* 1 + 132* 10 + 231* 0 + 308* 2 = 2020
84* 12 + 132* 3 + 231* 0 + 308* 2 = 2020
84* 9 + 132* 2 + 231* 3 + 308* 1 = 2021
84* 6 + 132* 1 + 231* 2 + 308* 3 = 2022
84* 6 + 132* 1 + 231* 6 + 308* 0 = 2022
84* 6 + 132* 8 + 231* 2 + 308* 0 = 2022
84* 17 + 132* 1 + 231* 2 + 308* 0 = 2022
Bonjour,
Une fois qu'on a vu que le millésime de l'année en cours est candidat à la solution, on se dit qu'on l'a plus que probablement trouvée...et c'est d'autant plus frustrant quand on n'arrive pas à le prouver.
Je propose quand même :
S = 2017
2018 = 1 * 308 + 2 * 231 + 5 * 132 + 7 * 84
2019 = 0 * 308 + 1 * 231 + 4 * 132 + 15 * 84
2020 = 2 * 308 + 0 * 231 + 3 * 132 + 12 * 84
2021 = 1 * 308 + 3 * 231 + 2 * 132 + 9 * 84
2022 = 0 * 308 + 2 * 231 + 1 * 132 + 17 * 84
Mais je suis curieux de voir si ceci peut être prouvé mathématiquement.
Merci et bon weekend, littleguy !
Bonjour à tous.
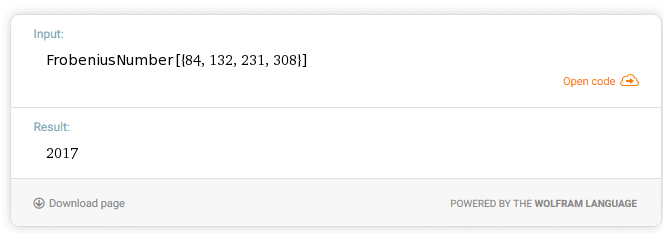
S = 2017 centimes d'euro.
Les sommes suivantes s'obtiennent ainsi :
| Somme | 84 | 132 | 231 | 308 |
| 2018 | 7 | 5 | 2 | 1 |
| 2019 | 15 | 4 | 1 | 0 |
| 2020 | 12 | 3 | 0 | 2 |
| 2021 | 9 | 2 | 3 | 1 |
| 2022 | 17 | 1 | 2 | 0 |
Merci pour l'énigme.
Bonjour,
Plus facile que la géométrie !!!
Je trouve S=2772 centimes
Pour payer 2773 centimes, il faut 8 coupures de 84 centimes, 6 coupures de 132 centimes, 3 coupures de 231 centimes et 2 coupures de 308 centimes.
Pour payer 2774 centimes, il faut 5 coupures de 84 centimes, 5 coupures de 132 centimes, 2 coupures de 231 centimes et 4 coupures de 308 centimes.
Pour payer 2775 centimes, il faut 2 coupures de 84 centimes, 4 coupures de 132 centimes, 1 coupure de 231 centimes et 6 coupures de 308 centimes.
Pour payer 2776 centimes, il faut 10 coupures de 84 centimes, 3 coupures de 132 centimes, 4 coupures de 231 centimes et 2 coupures de 308 centimes.
Pour payer 2777 centimes, il faut 7 coupures de 84 centimes, 2 coupures de 132 centimes, 3 coupures de 231 centimes et 4 coupures de 308 centimes.
Nota : parfois, les possibilités de payer ne sont pas uniques....mais comme il n'était demandé de toutes les indiquer .....!!!
Damned !!!!
J'ai oublié qu'il était possible de ne pas utiliser une ou plusieurs coupures..
Pour 2772 centimes il suffit d'utiliser 21 coupures de 132 centimes ..
La bonne réponse est 2017 !!!
Voilà ce qui arrive quand on veut répondre dans un demi sommeil !!! 
Bonsoir
S=2772
2773=8x84+6x132+3x231+2x308
2774=16x84+5x132+2x231+1x308
2775=13x84+4x132+1x231+3x308
2776=10x84+3x132+4x231+2x308
2777=18x84+2x132+3x231+1x308
La plus grande somme que l'on ne peut pas payer est S=2017.
Et pour payer de 2018 à 2022 : voir tableau
Bonjour
J'étais parti de l'idée complètement saugrenue qu'il fallait au moins une pièce de chaque.
Bien sûr S=2017
La plus grande somme d'argent S exprimée en centimes d'euro qu'ils ne peuvent pas payer exactement est 2017 centimes.
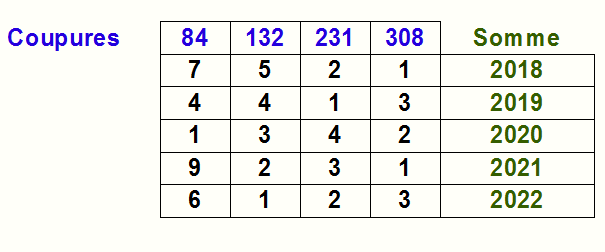
On peut payer :
S+1 = 2018 = 7*84 + 5*132 + 2*231 + 308
S+2 = 2019 = 15*84 + 4*132 + 231
S+3 = 2020 = 12*84 + 3*132 + 2*308
S+4 = 2021 = 9*84 + 2*132 + 3*231 + 308
S+5 = 2020 = 17*84 + 132 + 2*231
J'ai déduit ces résultats en calculant les sommes de 0 à 10000 (c'est faisable en O(rn) où r est le nombre de coupons et n la somme la plus grande). Mais aurait-on pu déduire le 2017 de manière plus mathématique? Comment cet exercice a-t-il été construit? Cela reste un mystère pour moi 
.
On peut vérifier que les 84 sommes de 2018 incluse à 2101 incluse sont payables exactement; c'est donc le cas aussi pour toutes les sommes supérieures à 2101, puisque la différence avec l'une des 84 sommes est multiple de 84.
Par exemple 7000=2044+59*84
Et pour (clic mauvais ..)
84 132 231 308
S+1 = 1850 5 5 2 1
S+2 = 1851 13 4 1 0
S+3 = 1852 10 3 0 2
S+4 =1853 7 2 3 1
S+5 = 1854 4 1 6 0
Bonsoir,
Merci pour cet exercice...
Je propose :
S=1885
S+1= 1886=308 + (2*231) + (4*132 )+ (7* 84)
S+2 = 1887 = (3*308) + 231 +(3*132) + (4*84)
S+3= 1888= (2*308)+(4*231) + (2*132) +84
S+4 = 1889 = 308 +(3*231)+ 132 + (9*84)
S+5 =1890 = (3*308)+(2*231)+ (6*84) (par exemple)
Comme 3*308=4*231=7*132=11*84=924, 1890 est réalisable sous diverses formes
Bonjour,
Apparemment il s'agit du problème de Frobenius 
pour lequel il existe des algorithmes de résolution. Je n'ai pas essayé de comprendre un algorithme, mais j'ai pu vérifier ma réponse, me voilà rassuré
S=2017
2018=7*84 +5*132+2*231+308
2019=4*84+4*132+1*231+3*308
2020=1*84+3*132+0*231+5*308
2021=9*84+2*132+3*231+1*308
2022=6*84+1*132+2*231+3*308
2019=15*84+4*132+1*231=4*84+11*132+1*231=4*84+4*132+5*231
2020=12*84+3*132+0*231+2*308=1*84+10*132+0*231+2*308=1*84+3*132+4*231+2*308
2022=17*84+1*132+2*231=6*84+8*132+2*231=6*84+1*132+6*231
bonjour,
Merci Littleguy
Clôture de l'énigme.
On trouve cet exercice sous une formulation très légèrement différente dans la finale internationale 2007-2008 du site de la fédération suisse des jeux mathématiques
Merci pour votre participation.
Bonjour,
trapangle et littlefox se posent la question d'une méthode mathématique .
Je donne quelques réflexions qu'ils ne manqueront pas d'exploiter:
ppcm(84,132,231,308) =924
produit des facteurs 11x7x4x3=924
somme des nombres 84+132+231+308 =755
924-755 =169
Et curieusement 2017 = 924+924+169 
> dpi
Curieusement ta formule ressemble au minorant de Davidson pour 3 "coupures" :
La tienne peut s'écrire :
, si
La Fédération suisse (problème 18 de la finale du 22ème championat) donne une explication qui tient compte des facteurs des coupures (après avoir prouvé que 2017 ne peut pas être atteint) :
Supposons que N > 2017. Il est classique (Bezout) que l'on peut écrire
N = a · 3 · 4 · 7 + b · 3 · 4 · 11 + c · 3 · 7 · 11 + d · 4 · 7 · 11
avec 0 ≤ a ≤ 10, 0 ≤ b ≤ 6, 0 ≤ c ≤ 3 et d un entier relatif
quelconque. On a alors
N = a · 3 · 4 · 7 + b · 3 · 4 · 11 + c · 3 · 7 · 11 + d · 4 · 7 · 11
≤ 3 · (11 · 3 · 4 · 7) − 3 · 4 · 7 − 3 · 4 · 11 − 3 · 7 · 11 − 4 · 7 · 11
+ (d + 1) · 4 · 7 · 11 = 2017 + (d + 1) · 4 · 7 · 11
donc d ≥ 0 ce qui prouve que N peut être atteint. Le plus grand
nombre à ne pas pouvoir être atteint est finalement 2017.
Pas simple tout ça
.
Au final, 2017 est un résultat particulier et l'exercice n'a pas été construit pour produire cette valeur particulière. On dirait que LittleGuy a sa petite liste de problèmes dont le résultat est 2017
.
Oups, il faut lire :
Pour la formule de dpi.
J'ai essayé cette formule avec les facteurs (2,5,7,11) au lieu de (3,4,7,11). Elle continue de fonctionner. 
La formule ci dessus peut être développée comme ceci :
Soit avec
alors :
Je pense que cette formule peut être prouvée d'une façon similaire à la solution de la Fédération Suisse. Mais c'est compliqué 
.
Les 20 premières sommes trouvées de cette façon sont :
383, 619, 737, 871, 893, 973, 1063, 1091, 1289, 1403, 1573, 1591, 1669, 1715, 1847, 1893, 2017, 2077, 2201 et 2263.
Il faudra donc attendre un peu avant la prochaine année : 2077 = g(2*5*9,2*5*11,2*9*11,5*9*11) 
Cette série n'est pas dans l'oeis.org
Merci pour ces brillantes démonstrations.
J'ai longtemps buté sur 1849=924x2+1 d'où mon poisson ,2017 étant effectivement à la mode ,j'aurais dû aller jusque là.
Peut-on aller jusqu'à dire que la solution est 3 ppcm-somme?
Oui mais seulement quand gcd = 1 et que les facteurs sont de la forme abc,abd,acd et bcd.
Nombre de participations : 11
63,64 %36,36 %
4Temps de réponse moyen : 120:18:26.
Annuler
connectez vous