Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Niveau exercices
Partager :

Une équation

Posté par
Sylvieg Moderateur 24-07-23 à 18:10

Bonjour,
C'est un sujet déjà posé non résolu ; mais je ne l'ai pas retrouvé.
Résoudre dans l'équation suivante :
x2 + 23 = 2y

J'ai trouvé des solutions, mais sans savoir si ce sont les seules.

Posté par
dpire : Une équation 24-07-23 à 19:29

Bonjour,

 Cliquez pour afficher

Posté par
Sylvieg Moderateurre : Une équation 24-07-23 à 20:27

Les mêmes que moi

Posté par
thetapinch27re : Une équation 24-07-23 à 22:05

Bonsoir,

 Cliquez pour afficher

Posté par
thetapinch27re : Une équation 24-07-23 à 22:14

Erreur dans mon précédent message.

 Cliquez pour afficher

Peut-on éditer nos messages ?

Posté par
Sylvieg Moderateurre : Une équation 24-07-23 à 22:15

Bonsoir,
@thetapinch27,

Citation :
J'ai trouvé des solutions
Et dpi a trouvé les mêmes

Posté par
Sylvieg Moderateurre : Une équation 24-07-23 à 22:18

Messages croisés
Non, on ne peut pas éditer ses messages.
Seuls les modérateurs peuvent éditer un message. Ils le font par exemple si on oublie de blanker ou si un code LateX ou un lien a été mal tapé.

Je regarderai demain ce que tu proposes. Ça doit pouvoir aboutir.

Posté par
dpire : Une équation 25-07-23 à 08:18

Bonjour,
Je pense en observant les puissances de 2 que 11 est la dernière car ensuite l'écart de 23 sera constant pour les meilleurs scores
exemple  x=2^26  =67 108 864  ---> 67 108 864²+23
--->4 503  599 627 370 519
à rapprocher de   x^52 =4 503 599 627 370 496
il n'y a aucune chance de contrer cet handicap.

Posté par
LittleFoxre : Une équation 26-07-23 à 00:32

Aucune chance? Je ne suis pas aussi catégorique

Les solutions de l'équation x^2+a=2^y sont aussi solutions de la congruence x^2+a \equiv 0 \pmod{2^y}.

Il y a des méthodes pour calculer cette congruence. Par exemple (en anglais):

On y montre que a \equiv -1 \pmod{8}, en effet le seul résidu quadratique modulo 8 est 1.
On y montre aussi que pour 3 \le y, il y a exactement 4 racines. Si x est une racine alors -x, 2^{y-1}+x et 2^{y-1}-x sont les 3 autres.
Et finalement que ces racines peuvent être générées récursivement. En effet, si x^2 + a \equiv 0 \pmod{2^y} alors soit x^2+a \equiv 0 \pmod{2^{y+1}}, soit (x + 2^{y-1})^2 + a \equiv 0 \pmod{2^{y+1}}.

Voici un graphique de x^2+23 pour chaque racine x.

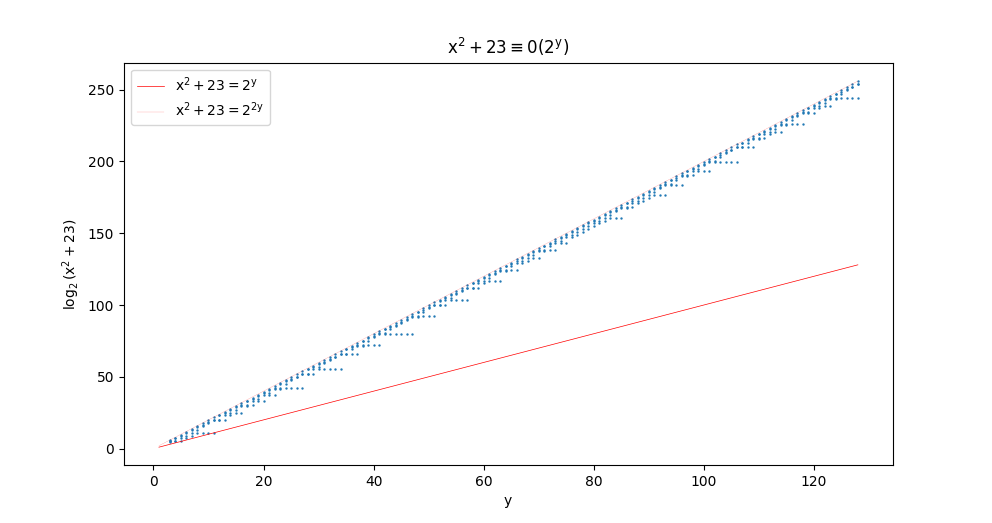
Une équation

On voit que x^2+23 reste très proche de 2^{2y}. En particulier x^2+23 \ge 2^{2(y-16)} pour y \le 25000. Les plus grand écarts étant donnés par :
x^2+23 \approx 2^{2(2949 - 15.29 )}
x^2+23 \approx 2^{2(7057- 15.09)}
x^2+23 \approx 2^{2(16874- 15.80)}
x^2+23 \approx 2^{2(20740- 15.73) }

Si x^2+23 = 2^y \ge 2^{2(y-16)} alors y \le 32 et les solutions sont relativement petites.

Ça a l'air vrai pour tous les a. Par exemple x^2+7=2^y a 5 solutions:
1^2 + 7 = 2^3
3^2 + 7 = 2^4
5^2 + 7 = 2^5
11^2 + 7 = 2^7
181^2 + 7 = 2^{15}

L'écart le plus important (pour y \le 25000) étant x^2+7 \approx 2^{2(15792-15.75)}.

Ce n'est pas une preuve que ce sont les seules solutions. Mais si on prouvait que cet écart est relativement petit (<<y/2) alors on aurait une limite sur la taille des solutions.

Posté par
dpire : Une équation 26-07-23 à 08:14

Pratiquement avec 23 on voit bien que 45²+23 = 2048 = 2^11
Observons les puissances de 2 suivantes et leur racine entière:
12  ---> 64   pas de reste  ainsi que toutes les puissances paires...
13 ---->90    reste 92  
15----->181 reste 7
17----->362  reste 28
19---->724   reste 112
21---->1448 reste  448
En  extrapolant  on ne trouve plus de reste =23

Posté par
dernyre : Une équation 26-07-23 à 13:20

Bonjour
J'avais étudié plusieurs cas mais pas celui là. Si on remplace 23 par 7 j'ai toutes les solutions. Il y en a une infinité et toutes les solutions se calculent par récurrence en partant de la première solution.

Posté par
LittleFoxre : Une équation 26-07-23 à 15:32

Je suis intéressé de voir ça. Je ne trouve que 5 solutions si on remplace 23 par 7.

Posté par
dernyre : Une équation 26-07-23 à 16:03

Je dois m'absenter mais à ce soir.
Pour 23 je ne suis pas sûr qu'on trouve. Par contre il y a une infinité de solutions du genre :
4995² - 2*3532² = - 23
8935² - 2*6318² = - 23

Posté par
dpire : Une équation 26-07-23 à 19:38

Pour 7 je suis d'accord avec

 Cliquez pour afficher

Posté par
dpire : Une équation 26-07-23 à 19:40

blanké au lieu de gras

Posté par
dernyre : Une équation 26-07-23 à 21:14

Bonsoir
En fait j'avais étudié l'équation Pell-Fermat x² - 2y² = - 7 qui a une infinité de solutions. Effectivement seuls quelques cas donnent pour y une puissance de 2.  J'ai 4 cas et non 5. Pouvez-vous les donner ?

Posté par
dernyre : Une équation 26-07-23 à 21:40

Elles sont plus haut

Posté par
dpire : Une équation 27-07-23 à 09:07

Bonjour,
Les nombres premiers ajoutés à un carré pour donner une puissance de 2 sont assez rares.
Voici pour n<100
Une équation

Posté par
Sylvieg Moderateurre : Une équation 27-07-23 à 10:20

Intéressant.
7-3, 23-7, 31-23, 47-31, 79-47 et 79-71 sont des puissances de 2
71-47 fait exception.
Une coquille : 512 = 29.

Posté par
jandri Correcteurre : Une équation 27-07-23 à 10:24

@dpi

je suis d'accord avec ta liste de nombres premiers mais j'ai relevé deux coquilles :
pour p=7 c'est la puissance 3
pour p=71 c'est la puissance 9

Les nombres premiers obtenus sont congrus à 7 modulo 8 (excepté le premier égal à 3).
On peut continuer avec p=103, p=127 et p=151.
Mais pour p=167 je ne trouve pas de solution (je n'ai pas démontré qu'il n'y en a pas).

Posté par
dpire : Une équation 27-07-23 à 12:28

Merci pour vos corrections.
En remerciements
Jusqu'à 5000:

Une équation

Posté par
dpire : Une équation 27-07-23 à 12:33

un zéro de trop....500
éventuellement je peux essayer

Posté par
LittleFoxre : Une équation 28-07-23 à 03:57

Voici la liste des solutions pour a=p < 5000 et y < 1000:

 Cliquez pour afficher


Je préfère 'a' à 'p'. Il n'y a aucune raison que ce terme soit premier.  J'ai par exemple des solutions pour 135, 175, 399.
Il ne doit même pas être impair.
Mais s'il est pair, alors il est soit 2 et la seule solution est 0^2 + 2 = 2^1, soit un multiple de 4 et les solutions de x^2 + a = 2^y  sont celles de (\frac{x}{2})^2 + \frac{a}{4} = 2^{y-2}. On peut dire que les solutions primitives ont a impair ou égal à 2.
S'il est impair et que y \ge 3, alors a \equiv -1 \equiv 7 \pmod{8}.

Il semble en effet qu'il n'y ait pas de solution pour a=167. En tout cas, il n'y en a pas pour y < 10000 (pas de typo, c'est bien quatre zéros ).
On voit aussi qu'il n'y a pas de solution avec y > 22 (pour a < 5000 sinon, il y a le trivial (2^{y'}-1)^2 + (2^{y'+1} - 1) = 2^{2y'} qui permet de faire monter y d'autant que l'on veut).

Comme d'habitude, le code est disponible ici:

Posté par
dpire : Une équation 28-07-23 à 08:02

Bon,
Sylvieg va être satisfaite ,on a fait le tour de la question

Comme on s'était intéressé à 23 e 7 je suis resté sur les premiers...
Pour +5000
5503  
11 585²=134 212 225--->+5503=134 217 728 = 2^27

Posté par
Sylvieg Moderateurre : Une équation 28-07-23 à 10:22

Bonjour,
Merci pour toutes vos réponses.
Cependant, je ne suis pas totalement satisfaite
Il semble confirmé que les seules solutions entières de x2 + 23 = 2y soient celles données par dpi au début du sujet.
Mais... ce n'est pas démontré me semble-t-il.

@LittleFox,
Quelque chose m'échappe sans doute dans ton tableau car il y a au moins une solution non nulle pour 4, 16, 64, 256, 1024 et 4096.
Le tableau la donne pour 4, mais pas pour les autres.

Posté par
LittleFoxre : Une équation 28-07-23 à 11:27

@Sylvieg
Bien vu, il y avait un bug

(2^{t-1}x)^2 + 2^{t}a = 2^{t}2^y au lieu de (2^{t/2}x)^2 + 2^{t}a = 2^{t}2^y.
J'ai codé les a pairs à 3h du matin

Le code est corrigé, voici la liste (70 solutions en plus):

 Cliquez pour afficher

Posté par
jandri Correcteurre : Une équation 28-07-23 à 11:41

Pour le problème initial je ne sais pas démontrer qu'il n'y a que deux solutions dans \N.

Pour la généralisation à l'équation x^2+a=2^y on peut se limiter aux solutions non nulles.
Comme l'a dit LittleFox le cas où a est pair est sans intérêt car il n'y a pas de solution pour a=2 et sinon on peut tout diviser par 4 un certain nombre de fois pour arriver au cas où a est impair.

A part les cas triviaux a=1 et a=3 on voit alors que pour qu'il y ait une solution il faut a\equiv7\pmod8.

La première valeur de a\equiv7\pmod8 telle qu'il n'y a pas de solution est a=95 et c'est facile à démontrer car il n'y a pas de solution avec y pair (on écrit une différence de deux carrés) et pas de solution avec y impair car 2 n'est pas un carré modulo 19.

Posté par
LittleFoxre : Une équation 28-07-23 à 14:50


Une preuve de la non existence de solution pour a=519 est donnée sur le site de l'oeis: . On peut l'étendre à tous les a.

Soit y = 2y':
\\ \Rightarrow x²+a=(2^{y'})^2 \\ \Rightarrow (2^{y'})^2 - x^2 = a \\ \Rightarrow (2^{y'})^2 - (2^{y'}-1)^2 \le a \\ \Rightarrow 2^{y'+1} - 1 \le a \\ \Rightarrow y' \le \log_2(a + 1) - 1 = \log_2(\frac{a}{2} + \frac{1}{2}) \\ \Rightarrow y \le 2\log_2(\frac{a}{2} + \frac{1}{2}) \\

Il y a donc un nombre (très) limité de y possibles, qu'il suffit de tester.

Pour a=519, y est pair puisqu'on a x^2 + 519 \equiv 2^y \equiv 1 \pmod{3}

Pour a=23, au contraire, y est impair puisqu'on a x^2+23 \equiv 2^y \equiv 2 \pmod{3}

Il reste a étendre la majoration de y à y impair. Mais je coince

Posté par
dpire : Une équation 28-07-23 à 16:41

De mon coté je cherche de "grands" y avec toujours mes nb premiers.
Littlefox  cherchait  y>23  , pour  n<5000 non , mais en suivant

5503-->y=27 avec 11585²

J'ai testé les premiers >10 000
j'ai 10567 et 10663
149²+10567 =32768=2^15
347²+10663 =131072=2^17
je laisse le chantier ouvert  pour chercher de temps en temps...

Posté par
LittleFoxre : Une équation 28-07-23 à 17:01

@dpi
Voici des nombres premiers avec y "grand" à toi de trouver le lien entre eux 


4095² + 8191 = 2^24
65535² + 131071 = 2^32
262143² + 524287 = 2^36

Posté par
jandri Correcteurre : Une équation 28-07-23 à 17:09

Littlefox

Les cas où a est impair et possède un diviseur premier congru à 3 ou 5 modulo 8 sont très simples puisque 2 n'étant pas un carré modulo a il en résulte que y est pair et il suffit de factoriser a pour trouver toutes les solutions.

Quand a a tous ses diviseurs premiers congrus à 1 ou 7 modulo 8 je ne sais pas faire.

Posté par
dpire : Une équation 29-07-23 à 11:51

>Littlefox ,
Je dirai p²-1+2p-1
Dans mon choix de 2p-1  premier, le suivant sera:
1 073 741 823²+2 147 483 647 =2^60

Posté par
LittleFoxre : Une équation 29-07-23 à 12:33

Effectivement, ce sont des nombres premiers de Mersenne et donc de la forme 2^p-1 😉


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !