Inscription / Connexion Nouveau Sujet
Une intersection.
Bonjour,
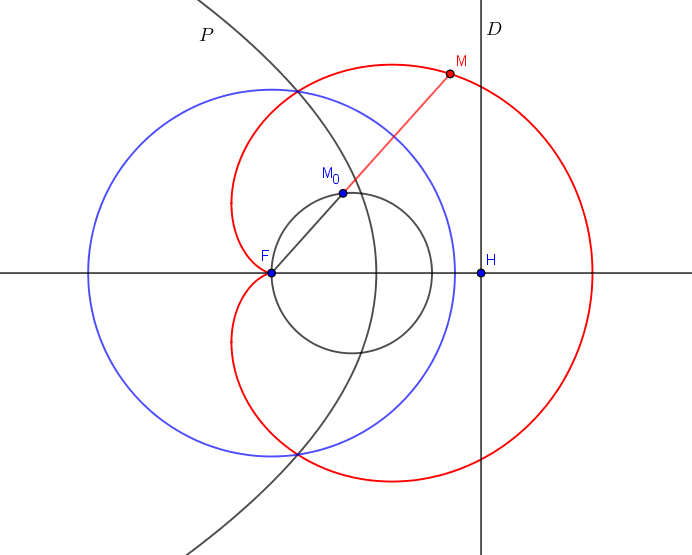
La figure représente la section d'un cône de révolution de sommet et d'une sphère de centre
par le plan défini par l' axe du cône et le centre de la sphère.
La sphère est tangente à une génératrice du cône.
On projette la courbe intersection cône/sphère sur un plan perpendiculaire à l'axe du cône.
Quelle est la courbe obtenue?

Plusieurs approches sont possibles:
- Le tout analytique.
- La géométrie descriptive.
- La géométrie dite synthétique.
J'avais trouvé la solution géométrique très belle. C'est pour elle que je partage cet exercice avec vous 
Bonjour veleda, bonjour mathafou,
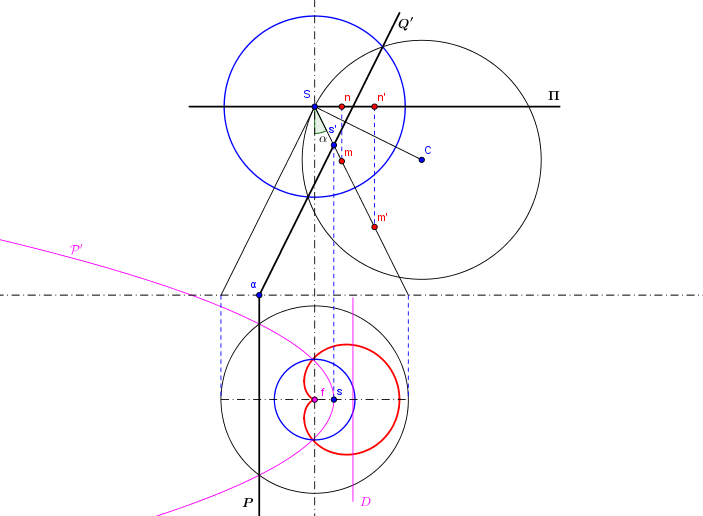
Oui, des inversions: votre "instinct" ne vous trompe pas.
Une solution avec un petit bémol dont je viens de me rendre compte à l'instant:
 Cliquez pour afficher
Cliquez pour afficherbonsoir lake
merci pour la solution que je la lirai demain,
comme je n'avais pas terminé la démonstration géométrique j'ai calculé,c'est assez simple mais pas très joli
je posterai l'équation trouvée demain car ce soir la touche blank ne marche plus
Bonjour veleda,
Oui avec une petite erreur de frappe; un à la place d'un
:
Qui est bien l'équation d'une cardioïde.
A quoi correspond ton ? J'imagine qu'il dépend du rayon de la sphère...

Finalement, je pense qu'il n'y avait pas d'erreur (échange et
); tout dépend de ton repère de départ: échanger
et
revient à une rotation d'un quart de tour autour de l'origine.
Néanmoins, je tombe, avec tes notations sur l'équation suivante:
avec
des puissances de sinus qui différent.
J' ai pu me tromper bien sûr mais ça colle avec Geogebra 
Moi j'étais partit sur des coordonnées cartésiennes, ça se passe bien et ça ressemble à une cardioïde mais de là à le prouver... ^^
Soit un cône d'équation et la sphère d'équation
.
La sphère est bien tangente au cône.
Leur intersection est donnée par les équations :
En faisant varier z on obtient une cardioïde mais c'est pas évident à partir des équations 
Bonjour Littlefox,
la sphère d'équation
Oui, tu développes pour obtenir:
Avec l' équation du cône, tu élimines
Puis élévation au carré pour obtenir:
qui est une équation de la projection de la courbe intersection sur
Avec tes
On a

bonjour,
>>lake
c'est certainement moi qui ai fait une erreur,je n'aime guère les calculs
as-tu trouvé une démonstration pour la propriété que tu utilises relative à la projection d'une parabole?

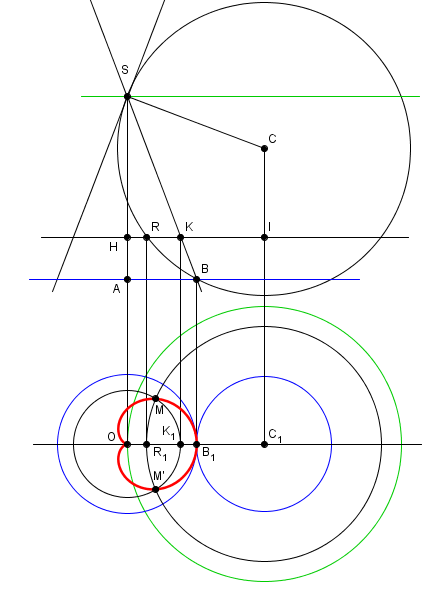
 )son plan tangent en S' diamétralement opposé à S
)son plan tangent en S' diamétralement opposé à S