Niveau algorithmique

Variations de liste de nombre

Posté par
NervaL928 11-11-15 à 17:11

Bien le bonjour
J'ai actuellement un problème d'info assez basique en soi mais avec lequel j'ai un peu de mal ^^"

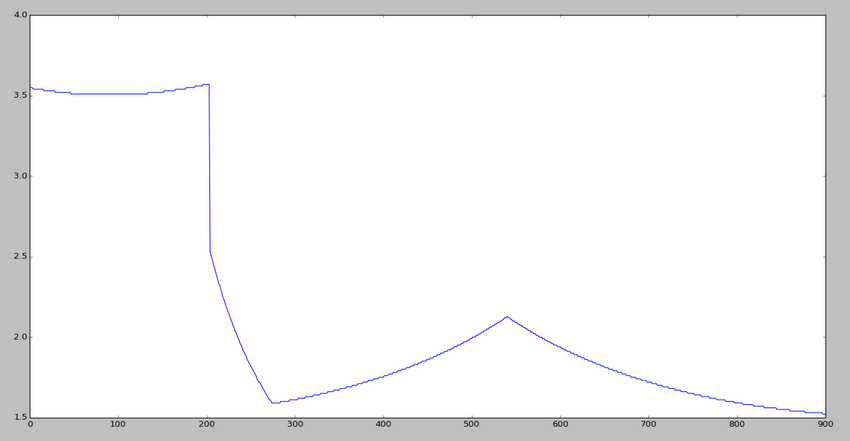
J'ai une liste de (beaucoup de) nombres que je peux tracer (cf image). On voit que vers $x=200$ on a une espèce de discontinuité. Je voulais donc savoir si c'était possible de détecter les changements de variation (par exemple en $x=270,535$ ) sans se faire avoir par les discontinuités ? Hélas (et mon cliché n'est pas assez bien pour ce problème), il se peut que "ça" soit croissant puis après "encore plus croissant" (ou décroissant et décroissant++)... Mon but final est en fait de faire une espèce de "linéarisation" de la liste, c'est-a-dire qu'elle soit en fait des segments de droites accolés (donc de la transformer en ligne brisée, continue par morceaux).

Merci de vos conseils

Variations de liste de nombre

Posté par re : Variations de liste de nombre 12-11-15 à 20:07

Coucou !
Pour détecter les changements de variation peut être que tu peut t'y prendre de cette manière :
Il y a changement de variation en $x_i$ si

$x_{i-1} \leq x_i$ et $x_{i-2} \geq x_{i-1}$

OU

$x_{i-1} \geq x_i$ et $x_{i-2} \leq x_{i-1}$

ET

$x_i \leq x_{i+1}$

OU

$x_i \geq x_{i+1}$

La première condition impose un changement de monotonie entre deux valeurs consécutives et la seconde impose que cela vaut sur au moins deux points. (Donc sur un morceau de courbe)

Tu peux par exemple commencer par utiliser un booléen qui vaudra True si la fonction était croissante jusqu'à présent et False sinon. Ainsi les condition 1 et 2 devrait être facile à écrire.

Bien sûr n'étant absolument pas informaticien, il doit exister des solutions bien plus efficaces, mais celle-ci a au moins le mérite de marcher. (enfin je crois)

Posté par re : Variations de liste de nombre 15-11-15 à 15:49

Oui j'avais essayé ça mais je me suis heurté à deux problèmes majeurs :
- la liste a tendance à être constante localement (dû à la façon dont elle est générée) ; pour mieux m'exprimer, voici la liste qui a généré le graphique d'au-dessus : http://pastebin.com/vwqfjm0r
- surtout, si j'interpolais tous ces points par une fonction continue (dérivable), cette méthode ne détecterait pas les variations de la dérivée elle-même ! (j'ai d'ailleurs pensé à une interpolation lagrangienne, mais un polynôme de degré 900 ça fait lourd à calculer, surtout qu'ici j'ai des discontinuités...)