Inscription / Connexion Nouveau Sujet
voile
bonjour
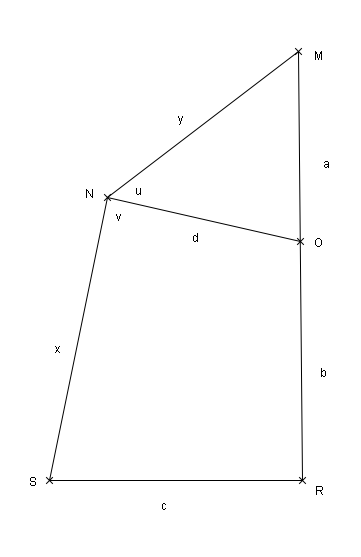
le quadrilatère symbolise une voile
les longueurs a, b, c et d sont données et le triangle ROS est rectangle en R
déterminer x et y en fonction de a, b, c et d de façon que les angles u et v soient égaux
il n'est pas nécessaire de blanker ...
merci par avance ...
Bonjour,
Sur ma figure,je ne trouve pas de possibilités
que u = v ce qui veut dire que a doit déja
avoir un rapport élevé par rapport à b et c par exemple>leur moitié
on m'a posé ce pb et je n'ai pas la réponse ...
Al-Kashi dans les triangles NOM et SON permet d'obtenir une relation entre x et y si on veut que u = v (donc cos u = cos v) (certe pas linéaire...)
mais je ne vois pas d'aurtres relations "simples" entre x et y ...
on peut remarquer que N appartient au cercle de centre O et de rayon d donc en faisant "tourner N autour de O" il semblerait qu'il y ait pourtant une solution ...
je n'ai d'autre part aucune idée des valeurs respectives de a,b,c et d ...
mais en supposant des conditions nécessaires sur ces longueurs peut-on répondre à ma question ....
to be continued ....
à carpediem
Oui j'ai des solutions géométriques si le rapport a/b
et a/c est supérieur à 0.5,mais pas encore trouvé de
relations (c'est un pb pour frenicle )
)
Bonjour carpediem
Je donne des dimensions qui conviennent
pour construire une figure qui pourra servir
à trouver les ratios.
Mais à priori,il y a une impossibilité de
trouver x et y avec a b c et d donnés au hasard,le problème exige que a,b,c,et d soient déja "compatible".
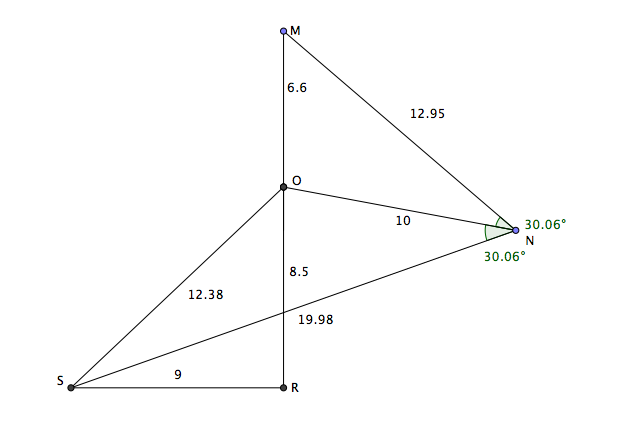
Ma figure : a=6 b=5 c= 4 d= 4.222-->x=y=61°61
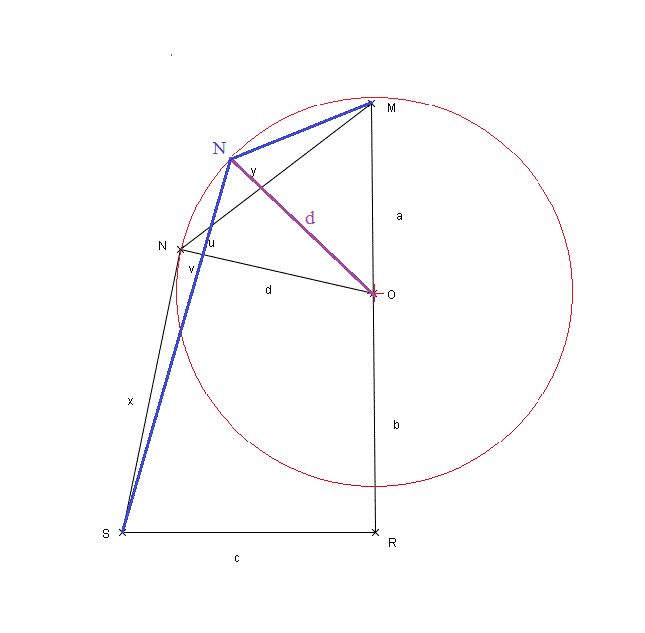
Al Kashi dans les triangles NOM et SON.
a² = d² + y² - 2.d.y.cos(u)
c²+b² = d² + x² - 2dx.cos(u)
(d² + y² - a²)/(2dy) = (d² + x² - c² - b²)/(2dx)
x.(d² + y² - a²) = y.(d² + x² - c² - b²)
---
Al Kashi dans le triangle SNM :
(a+b)² + c² = x² + y² - 2xy.cos(2u)
cos(u) = (d² + x² - c² - b²)/(2dx)
cos(2u) = 2cos²(u) - 1
cos(2u) = (d² + x² - c² - b²)²/(2d²x²) - 1
(a+b)² + c² = x² + y² - 2xy.[(d² + x² - c² - b²)²/(2d²x²) - 1]
---
On a donc le système de 2 équations à 2 inconnues x et y :
(a+b)² + c² = x² + y² - 2xy.[(d² + x² - c² - b²)²/(2d²x²) - 1]
x.(d² + y² - a²) = y.(d² + x² - c² - b²)
(a+b)² + c² = x² + y² - 2xy.(d^4 + x^4 + c^4 + b^4 + 2d²x² - 2c²d² - 2b²d² -2c²x² - 2b²x² + 2b²c² - 2d²x²)/(2d²x²)
x.(d² + y² - a²) = y.(d² + x² - c² - b²)
(a+b)² + c² = x² + y² - xy.(d^4 + x^4 + c^4 + b^4 - 2c²d² - 2b²d² - 2c²x² - 2b²x² + 2b²c²)/(d²x²)
x.(d² + y² - a²) = y.(d² + x² - c² - b²)
d²x²((a+b)² + c²) = d²x^4 + d²x²y² - xy.(d^4 + x^4 + c^4 + b^4 - 2c²d² - 2b²d² - 2c²x² - 2b²x² + 2b²c²) (1)
x.(d² + y² - a²) = y.(d² + x² - c² - b²) (2)
Il reste à regrouper les termes en puissance de y dans l'équation (1)
L'équation (1) sera du second degré en y et on pourra donc exprimer y en fonction de x.
Et puis en remplaçant y par ce qui sera trouvé dans (2) ...
-----
Je n'ai évidemment rien vérifié dans ce que j'ai écrit.

à JP
Quel courage !
en me relisant bien sûr u=v =61°607
pour mémoire x=8.878 et y =3.493
Al Kashi confirme t-il,
salut et merci J-P
que suis-je bête, hé oui Al-Kashi dans le triangle MSN, j'y avais pensé mais je n'avais pas poursuivi l'idée (trop fugace  )...
)...
je vais reprendre cela et essayer de finir proprement
merci encore 
Bonjour à tous,
Félicitations JP 
(sur le site Wolfram, ils ne pourraient pas expliciter ce 'petit' système ? )
J'ai pris la même voie avec le trinagle SMN, mais je n'ai pas eu ton courage pour aller jusqu'au bout....
J'examine la piste par les aires : SRM (facile) + SNM (avec x,y et 2u) = SOR (facile) + SNO (avec x, d et u)+ NMO (avec y, d et u)
On verra ce week-end...
Ca vaut un **** dans les énigmes !!!
Je suis curieux de voir si une formulation explicite 'simple' pourra être dégagée par l'un d'entre nous !!!
De même qu'une formulation des conditions d'existences de solutions...
A+ et bon courage
bonjour,
>>rumbafan j'ai cherché moi aussi avec les aires et sauf erreur de calcul je trouve la relation
mais comme le soleil était revenu je suis sortie et j'en suis restée là et je n'ai pas beaucoup de courage pour reprendre les calculs
Bonsoir,
considérons la figure suivante:
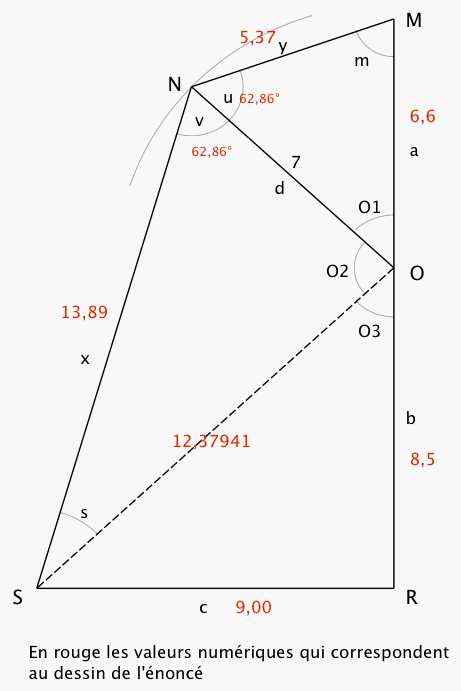
suivant la loi des sinus pour les triangles quelconques nous avons
x/sin(O2) = OS/sin(v) = d/ sin(s) dans le triangle SNO
et y/sin(O1) = a/ sin(u) = d/ sin(m) dans le triangle NMO
u = v (condition de l'énoncé) La somme des angles du quadrilatère SNMR vaut 2 donc u+v+m+s+(
donc u+v+m+s+( /2-O3)=3/2*
/2-O3)=3/2* ou 2u+v+s-O3=
ou 2u+v+s-O3= (relation 1)
(relation 1)
sin(s)=d*sin(u)/OS on a s=arc sin(d*sin(u)/OS) et sin(m)=d*sin(u)/a ou m= arc sin (d*sin(u)/a)
O3 = arc tg (c/b)
Remplaçons dans la relation 1:
2u + arc sin(d*sin(u)/OS)+ arc sin (d*sin(u)/a)- arc tg (c/b) = 
avec OS = (b2+c2)
(b2+c2)
Avec les valeurs de l'énoncé on fait varier u dans un tableur et l'on trouve u= 62,86°
on déduit sin(O1)= sin( -u-m) donc y=a*sin(O1)/sin(u)
-u-m) donc y=a*sin(O1)/sin(u)
et sin(O2)= sin( -u-s) donc x = OS*sin(O2)/sin(u)
-u-s) donc x = OS*sin(O2)/sin(u)
Pour les conditions de l'énoncé y=5,374 et x=13,891
Bien à vous
à veleda,
Ta formule ne fait pas apparaitre b
est-ce normal?
à castoriginal,
Beau travail (comme toujours).
J'ai bâti une figure qui semble aussi convenir,
Il suffit de prolonger SO jusqu'à S' symétriquee de S
et de mettre N dans l'alignement de MS'sur la pependiculaire
en O.
Mais j'avoue ne pas avoir trouvé la formule
qui relie abcd x et y pour avoir u=v
bonjour,
>>dpi,
j'ai calculé de deux façons l'aire du quadrilatère SOMN
1)S=aire SOMN=aireSON+ aireNOM si u= v ces deux triangles ont pour hauteur d.sin(u) relativement aux côtés NS et NM donc
S=
2)S=aireSMN+aireSOM
aireSNM=
aireSOM=
d'où
S=
d'où
c'est bien ce que j'avais trouvé hierj'espère ne pas faire deux fois la même erreur
Bonjour,
la formule de veleda est bonne, et avec les trois al Kashi dans SON, NOM et SOM (données par JP), on obtient le système suivant (partant du principe que les deux angles sont égaux à u):
(x+y)d cos(u) = d²- ab + xy cos (2u) -> avec Al Kashi
(x+y)d sin(u) = ac + xy sin (2u) -> avec les aires
On ne peut que remarquer la beauté et la similitude de ces deux égalités.
Je n'ai pas encore trouvé de façon de faire disparaitre les angles, mais je cherche encore. Peut-être dans les complexes ?
Juste pour lancer d'autres pistes. 
Bonjour à tous,
c'est bien de se poser la question de " je cherche encore mais je vais peut-être bientôt trouver " alors que je viens de vous montrer la solution qui est irréfutable !
Quid est ?
Castoriginal (dernier message Posté le 20-07-11 à 20:50)
Bonjour,
J'ai commencé comme suit :
Dans un système d'axes Oxy j'ai placé O en O(0;0) et N (-d;0) ces deux points étant considérés comme fixes
M décrit alors un cercle de rayon a et de centre O et en prenant MON =  on a
on a
M(-a cos ;a sin
;a sin )
)
et R (b cos ;-b sin
;-b sin )
)
S peut en être déduit car SR  RO et longueur RS = c
RO et longueur RS = c
==> la pente de NM étant connue, celle de SN est exactement l'opposée ==> on connait l'équation de la droite NS et on exprime que S lui appartient
Reste à éliminer  .... sans réintroduire u ou v
.... sans réintroduire u ou v 
J'ai déjà essayé... sans succès...peut-être que des expressions explicites
x= f1(a;b;c;d) sans u ou v
y= f2(a;b;c;d) sans u ou v
n'existent pas car j'ai toujours des termes contenant de la trigono et d'autres qui n'en contiennent pas !!!
Je continue mes recherches
A+
Bonjour Castoriginal,
Ta (très logique) démarche fait appel au tableur sur une valeur paticulière pour pouvoir continuer...
Un goal seek en faisant varier  dans les relations que J-P a données ou que d'autres ont gardé jalousement sur leur feuille de papier devrait également permettre de trouver une solution pour a b c d donné (dans certains cas, si ça foire ==> c'est qu'on n'est pas dans le cadre des conditions d'existence)
dans les relations que J-P a données ou que d'autres ont gardé jalousement sur leur feuille de papier devrait également permettre de trouver une solution pour a b c d donné (dans certains cas, si ça foire ==> c'est qu'on n'est pas dans le cadre des conditions d'existence)
Une application numérique ou la recherche d'une valeur particulière par un tableur ne répond pas tout à fait à l'énoncé ...aussi méritoire que ce soit
Pour répondre à l'énoncé, il faudrait trouver les fonctions explicites f1(a;b;c;d) et f2(a;b;c;d) (+ éventuellement les conditions d'existence  )
)
==> cela clôturerait magistralement ce sujet et nous pourrions nous attaquer à un autre  ... le plaisir est sans fin
... le plaisir est sans fin
Bonjour Veleda,
J'ai la même relation et c'est pour cela que je parle de termes avec et sans trigono qui empêchent d'expliciter...
Peut-être que pour la fin du week-end l'un d'entre nous aura eu l'IDEE simple que nous cherchons tous...
Trigonométriquement vôtre 
A+
Bonjour à tous,
J'ai cru comprendre que carpediem
voulait obtenir des angles u et v égaux en ayant
comme seules données a,b,c et d;alors
comme j'ai vu que cela était impossible
si a n'avait pas une valeur compatible,
j'ai comme castoriginal cherché 4 valeurs compatibles
et ensuite il est facile de trouver
x,y,u et v.
Bonjour à tous,
je comprends votre désir à tous de trouver des relations mathématiques explicites déterminant les inconnues x et y en fonction de a,b,c,d avec la contrainte d'angle u = v.
La méthode que j'ai expérimentée, malgré les commentaires de rejet de plusieurs d'entre vous, fait partie intégrante du domaine des mathématiques. Elle fait partie du domaine des mathématiques supérieures et j'en ai reçu les principes lors de mes années de candidature à l'Ecole Polytechnique de Bruxelles (ULB) dans les années 1960.
Les ordinateurs permettent de rapidement calculer les valeurs itératives qui autrefois étaient calculées à la main et prenaient beaucoup de temps.
Elles s'appliquent notamment à des équations de degré supérieur dont les racines sont multiples et difficiles à trouver ou à des équations trigonométriques complexes.
De grands mathématiciens tels Newton ou Gauss ont mis au point des méthodes itératives.
Si vous voulez en savoir plus voici quelques liens:![]() et
et
![]()
Amitiés
merci à tous pour vos efforts
juste qq rappels :
les points M, O et R sont alignés
la consigne (enfin ce qu'on m'a demandé) est d'exprimer x et y en fonction de a, b, c et d pour que u = v
d'autre part je plussoie aux propos de l'original castor qui propose une solution même si elle fait intervenir des valeurs particulières aux constantes a,b,c et d
l'important n'est-il pas d'exercer sa sagacité et sa réflexion sur un problème (tout à fait concret puisqu'il s'agit d'une voile (de bateau) mais je n'en sais pas plus))

à J-P : dans l'utilisation de la formule cos(2u) = ... n'y aurait-il pas une erreur dans le dénominateur (le carré conduit à 4d²x² ? ...)
bonsoir,
je fais remarquer à Carpediem que la solution que j'ai avancée n'est pas particulière aux valeurs a,b,c,d mentionnées qui n'ont été citées qu'à titre d'exemple.
Mes 3 équations sont valables pour tous les quadruplets a,b,c,d possibles.
Je rappelle ici mes 3 relations :
1)2u + arc sin(d*sin(u)/OS)+ arc sin (d*sin(u)/a)- arc tg (c/b) =
avec OS = (b2+c2)
(b2+c2)
2)sin(O1)= sin( -u-m) donc y=a*sin(O1)/sin(u)
-u-m) donc y=a*sin(O1)/sin(u)
3) sin(O2)= sin( -u-s) donc x = OS*sin(O2)/sin(u)
-u-s) donc x = OS*sin(O2)/sin(u)
PS: je vous signale que je suis sur une autre piste basées sur 2 théorèmes de la bissectrice
Amitiés, bonne nuit
Bonjour,
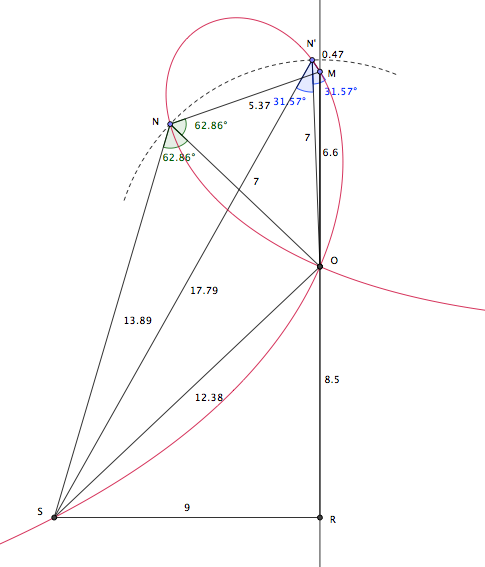
Le lieu des points d'où l'on voit les segments OM et OS sous un même angle est la strophoïde représentée en rouge sur le dessin.
Il se trouve qu'avec les données numériques de castoriginal, la boucle de cette strophoïde qui nous intéresse recoupe le cercle de centre O et de rayon 7 en deux points : le point N indiqué par castoriginal et un deuxième point N' très proche de M (voir le dessin).
Cela donne une approche géométrique des conditions de compatibilité : selon les positions respectives de la boucle de strophoïde et du cercle de centre O et de rayon d, il peut y avoir 0, 1 ou 2 solutions.
Bonjour,
J'avais bien dit que c'était un problème pour frenicle..
Cela confirme aussi qu'il n'y a pas toujours de solution
Comment cela pas de solution ?
Le chemin est tout à fait tracé dans ma réponse.
Il suffit de le suivre.
Elémentaire ... même si un peu ennuyeux.

Voici une formule explicite (en principe  )
)
A partir des longueurs données a, b, c, d (dans l'exemple de castoriginal a = 6,6, b = 8,5, c = 9, d = 7) on forme l'équation du quatrième degré :
Si t est une solution de l'équation (qu'on peut calculer en principe avec la formule de Ferrari...), on a :
et
Avec les données numériques ci-dessus, on obtient quatre solutions à l'équation dont deux correspondent au graphique de ce matin :
t = 0,018848765 x = 17,78812167 y = 0,475007027
t = 0,428963723 x = 13,89110820 y = 5,374032082
Les deux autres solutions correspondent à des points du mauvais côté de la voile.
Heureusement qu'il pleuvait ce matin 
> J-P
Il n'y a pas toujours de solution correspondant au problème posé par carpediem, qui précise la forme de la voile (le point N est à gauche de OM et au dessus de OS).
Par exemple, si a = 6,6, b = 8,5, c = 9 mais d = 10, on a cette solution où le point N est du mauvais côté :
C'est bien une voile, mais après un empannage un peu violent 
à JP
Ce que je veux dire peut s'expliquer ainsi:
soit b=7,c=4 et d=3
impose une seule dimension pour a
 3.5 et donc si l'énoncé
3.5 et donc si l'énoncé
donne a= 5 par exemple ,il n'y a pas de soluition
donc a,b,c,d doivent être compatibles
à frenicle
Nos réponses se sont croisées.
Merçi.
Il serait astucieux de trouver une table de compatibilité...
> dpi
Oui, mais j'ai un peu la flemme...
Par contre, ton exemple est mal choisi.
Avec a = 5, b = 7, c = 4 et d = 3 il y a une solution : x = 8,220252899 y = 4,765368318

>frenicle
Je voulais dire SO ce qui est plus
proche mais aussi idiot..
Ce n'est pas les lunettes mais Alz...mer
Bonjour à tous,
Dans la solution que j'avais donnée, je n'avais pas envisagé que l'angle m soit obtus. Grâce au dessin de frenicle, j'ai trouvé la modification de ma formule pour la deuxième solution.
1) m angle aigu
2u + arc sin(d*sin(u)/OS)+ arc sin (d*sin(u)/a)- arc tg (c/b) =
avec OS =(b2+c2)
sin(O1)= sin(-u-m) donc y=a*sin(O1)/sin(u)
sin(O2)= sin(-u-s) donc x = OS*sin(O2)/sin(u)
2) m angle obtus
2u + arc sin(d*sin(u)/OS)+ -arc sin (d*sin(u)/a)- arc tg (c/b) =
-arc sin (d*sin(u)/a)- arc tg (c/b) =
avec OS =(b2+c2)
sin(O1)= sin(-u-m) donc y=a*sin(O1)/sin(u)
sin(O2)= sin(-u-s) donc x = OS*sin(O2)/sin(u)
Bien à vous
on trouve alors u=v=31,574°



