Inscription / Connexion Nouveau Sujet
Le champ triangulaire.

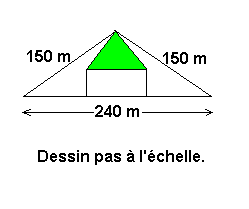
Un père veut partager un de ses champs entre ses 4 fils. Le champ est en forme de triangle isocèle.
Chaque enfant recevra, une partie ayant un aire représentant exactement le quart de l'aire totale du terrain.
Le plus vieux reçoit une parcelle rectangulaire, le plus jeune reçoit lui une parcelle en forme de triangle isocèle (en vert sur le dessin).
Question: Quel est le périmètre de la parcelle du plus jeune ?
-----
Bonne chance à tous. 
Clôture de l'énigme dimanche.


 L'aire du champ etant egale a 10800m² chaque enfant aura 2700m².
L'aire du champ etant egale a 10800m² chaque enfant aura 2700m².
En notant x la longueur de la base du triangle vert et est egalement la longueur du rectangle,y la larguer du rectangle et z la hauteur du triangle vert,on a un systeme a trois equations et trois inconnues :
y+z=90
xy=2700
(x+z)/2=2700
qui donne x = 90, y=30 et z=60.
donc le triangle vert a une base de 90m et une hauteur de 60m.
Donc en ramenant à un triangle rectangle en se servant de la hauteur on trouve la longueur du dernier coté :
par consequent le perimetre du triangle vert est :
90+2*75=240m!!
Voila voila, un petit exo pour bien debuter la journee!!
Miaouw


Le périmètre cherché vaut 240 m
Preuve
L' aire de la parcelle du plus jeune = m2 = 2700 m2
Appelons 2.a la longueur de la base du triangle isocèle-parcelle et b sa hauteur
On a donc a.b = 2700
Or, par Pythagore, la hauteur du champs vaut 90 m
la hauteur du rectangle est alors de 90 - b
L'aire du rectangle est de 2.a.(90 - b)
 2.a.(90 - b) = a.b
2.a.(90 - b) = a.b
2.(90 -b) = b d'où on tire b = 60
de là, a = 45
Le périmètre cherché vaut 2.a + 2.x où x est la longueur des côtés égaux de la parcelle du plus jeune
Pythagore : x =  [60² + 45²] = 75
[60² + 45²] = 75
Donc le périmètre = 90 m + 150 m = 240 m
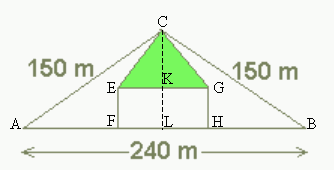
 Avec les notations de la figure ci-dessous
Avec les notations de la figure ci-dessous
en applelant l'aire du rectangle IJKL, chaque fils a une parcelle d'aire
et l'aire du triangle initial vaut
CIB est un triangle rectangle en I donc
L'aire de ABC vaut (1)
L'aire de IJKL vaut
L'aire de CJK vaut
Donc
Donc
L'aire du rectangle IJKL vaut
En combinant l'équation précédante avec l'équation (1) on aboutit à
La distance
Le périmètre de la parcelle du plus jeune fils vaut donc
 Ma réponse est : périmètre de la parcelle du plus jeune = 240 m
Ma réponse est : périmètre de la parcelle du plus jeune = 240 m
Voilà comment:
On calcule la surface totale, pour cela il nous faut la hauteur h. On sais que +
=
donc h = 90 m
Surafce totale = ()/2 = 10800
Donc surface de chaque part est 10800/4 = 2700
D'après le dessin, la base du triangle du plus jeune = longueur du rectangle du vieux = x
hauteur du triangle du plus jeune = 90 - largeur du rectangle du vieux = 90 - y
On = 2700
et /2 = 2700
-
= 5400
d'où x = 90 m et y = 30 m
La parcelle du plus jeune est un triangle isocèle de base 90 m et de hauteur 60 m. Donc le côté isocèle c = = 75 m
D'où périmètre = 75 + 75 + 90 = 240 m


 Soit S la surface du grand triangle. Son demi périmètre est égale à P=540/2 = 270
Soit S la surface du grand triangle. Son demi périmètre est égale à P=540/2 = 270
D'après Héron.
S =  (270*(270-240)*(270 -150)2) = 10800
(270*(270-240)*(270 -150)2) = 10800
La hauteur du grand triangle est donc égale à H = 2*S/240 = 90.
Soient L et l les dimensions du rectangle et h la hauteur du petit triangle .L*h/2 = L*l donc h= 2*l et comme h+l = H=90, on a h = 60.
L = (S/4) * 2/h = 90
Soit a la longueur du côté égal du petit triangle, et p' son demi périmètre, ona :
p' = 1/2 (2a + 90) = a + 45
J'utilise à nouveau la formule d'Héron dans le petit triangle s = 10800/4 = 2700 =  [(a+45) (a-45) 452] = 45 *
[(a+45) (a-45) 452] = 45 *  (a2- 452]
(a2- 452]
a2- 452 = 602
a2= 152 (42+32).
a = 15*5 = 75
Le périmètre du petit triangle est donc égal à 2 p' = 2a +90 = 240


 Le périmètre de la parcelle du plus jeune est de 240 m.
Le périmètre de la parcelle du plus jeune est de 240 m.
 On part avec la formule de Heron :
On part avec la formule de Heron :
où a,b,c sont les longueurs des côtés du triangle, p le demi-périmètre et S l'aire.
Dans le grand triangle, p = 540/2 = 270 m (demi-périmètre) puis S = 10800
Ainsi, chaque parcelle aura pour aire 2700 ( en divisant par 4, avec des parts égales ).
D'autre part, l'aire du grand triangle se calcule aussi via S =
ce qui nous permet de trouver la hauteur h relative au côté mesurant 240 m. h =
( résultat qu'on peut aussi aisément trouver par Pythagore dans le demi-triangle ).
Notons enfin x la longueur du rectangle et y la largeur.
L'aire du rectangle est : xy = 2700
L'aire du triangle vert est :
D'où le système :
L'unique solution est x = 90 et y = 30.
Ainsi la base du triangle vert est x = 90 m et sa hauteur relative est 90-y=60 m.
Reste à appliquer une fois le théorème de Pythagore dans un demi-triangle vert pour prouver
que les deux autres côtés du triangle mesurent 75 m ( )
Les côtés du triangle vert ( parcelle du plus jeune ) sont donc : 90m, 75m et 75m.
Conclusion: Le périmètre vaut ( 90 + 75 + 75 )
Bon, c'est fort peu élégant mais ça marche.
Par contre, il existe peut-être une solution donnant directement le périmètre
(sans le calcul des trois longueurs des côtés, mais je n'ai pas trouvé l'astuce...)
 La hauteur du champs à partager vaut
La hauteur du champs à partager vaut
L'aire totale à partager est donc 90*120=10800 et la part à chaque fils sera de 2700.
Si le champs rectangulaire a comme côtés x (sur la face du triangle de longueur 240) et y, on a xy=2700.
L'aire du triangle vert vaut (90-y)x/2=45x-xy/2=45x-1350=2700
D'où on en tire que la base du triangle vert vaut x=90 et que sa hauteur vaut 90-30=60. Par Pythagore on a son côté: c²=60²+45² => c=75
Finalement le périmètre du triangle vaut P=2c+x=240.
Mes calculs sont tout sauf beaux, mais je viens de rentrer de vacances  et j'ai du retard sur les énigmes, alors je fais un peu à la va-vite...
et j'ai du retard sur les énigmes, alors je fais un peu à la va-vite...
Isis


Bonjour
Périmètre du triangle : 2*75+90 = 240 m .


 Etant donné que le périmètre de la parcelle totale du terrain est de 150m+150m+240m, ce qui est égal à 540m, et que le père donne 1/4 de cette parcelle de terrain à chacun de ses quatre fils, le calcul est donc de 540/(1/4)= 540/4=135m. Le périmètre que chacun des fils, le plus jeune y compris est de 135m
Etant donné que le périmètre de la parcelle totale du terrain est de 150m+150m+240m, ce qui est égal à 540m, et que le père donne 1/4 de cette parcelle de terrain à chacun de ses quatre fils, le calcul est donc de 540/(1/4)= 540/4=135m. Le périmètre que chacun des fils, le plus jeune y compris est de 135m
 Je calcule la surface du grand triangle à l'aide de la formule de Héron
Je calcule la surface du grand triangle à l'aide de la formule de Héron
S= 10 800..Chaque part fera donc 2 700.
Le petit triangle et le rectangle ayant même surface, la hauteur du triangle est égale à deux fois la largeur du rectangle.
Comme la hauteur du grand triangle est égale à 90, la hauteur du petit triangle est égale à 60 et sa base 90.
Pour calculer les côtés égaux du petit triangle, j'utilise à nouveau la formule de Héron et je trouve que chaque côté est égal à 75.
Le périmètre de la parcelle du plus jeune (le petit triangle) est donc égal à :
90 + 75 + 75 = 240


 le périmètre de la parcelle du plus jeune est de 200 m.
le périmètre de la parcelle du plus jeune est de 200 m.


Réponse =240m
explications:
AL=240/2=120
AL²+CL²=AC²
Donc
CL=(150²-120²) ^ 0,5=(22500-14400)^0,5= 90
CL=90 m
L'aire GEFH=L'aire CEG
EF*FH=EG*CK
Ou
EF*FH=FH*(90-KL)/2=FH*(90-EF)/2
Donc
2EF=90-EF
ou
EF=30m
Donc
CK=90-30=60
L'aire ACEF=L'aire ACL/2=L'aire ACL-L'aire CKE -L'aire EFKL
L'aire ACL=90*120/2= 5400 m²
L'aire CKE=EK*CK/2=EK*60/2=30EK
L'aire EFKL=EF*EK=30EK
Donc:
5400/2=2700=5400-30EK-30EK
donc EK=45
FH=EG=45*2=90
CE²=CK²+EK²
CE=(60²+45²)^0,5=75
Périmètre CEG=EG+CG+CE=75*2+90=240m

Je nomme les trois sommets: B celui de gauche, A celui du haut, et C celui de droite
L'aire d'un triangle dont on ne connait que la mesure des trois cotés a, b et c est :
Ce qui donne pour le terrain du vieux:
= 10800
La hauteur issue de A va s'écraser en face sur [BC] en H
AH =
AH = 90m
Donc chaque parcelle a une aire de A/4 = 2700
Je nomme ensuite x la largeur du rectangle et y sa hauteur
h est la hauteur du triangle inscrit dans le premier
Les quatres parcelles ont la même aires:
Ce qui donne le système d'équation suivant:
(1) x*y = 2700
(2) = 2700
(3) y+h = 90
de (3), on tire: y = 90-h
En remplacant dans (1): x(90-h) = 2700
Et enfin en remplacant dans (2):
= 2700
Ce qui donne h = 60m
De la on en déduit y et x;
y = 90-h = 90-60
y = 30m
x = 2700/30
x = 90m
la base de la parcelle du plus jeune vaut donc:
= 75m
il ne reste plus que le coté du triangle:
Avec ce brave Pythagore qui ne c'était pas lever pour rien ce matin la:
= 75m
Et voila, le périmère final est donc:
150+75+30+75 = 330 mètres
Je suis désolé j'aurais bien utiliser LATEX pour le système d'équations mais je n'ai absolument pas compris les exemples !
 Aire du grand triangle = 18000 m², donc chacun aura 2700 m².
Aire du grand triangle = 18000 m², donc chacun aura 2700 m².
En exprimant l'aire du petit triangle en fonction de x (base) et y (hauteur) :
At = 1/2*x*y = 2700
Aire rectangle = x(90-y)=2700
=> x = 90 m, et y = 60 m.
Le perimètre est donc de 240 m.


 j'ai trouvé un perimetre de 180m...
j'ai trouvé un perimetre de 180m...
g droit a 1 smyley ? =)
 voila la reponse
voila la reponse
posons x hauteur du triangle isocele en vert
y le plus petit coté du rectangle
z le plus grand coté du rectangle
Premierement, sachant que la base du grand triangle isocele vaut 240 (donc 1/2*base = 120) et que les cotes de ce meme triangle vallent 150, en utilisant Pythagore on en deduit que la hauteur du grand triangle isocele est 90 (120²+ x² = 150², soit x=90).
Puis, avec les inconnus ainsi posés on doit resoudre le systeme suivant :
x+y (hauteur du triangle isocele en vert+le plus petit coté du rectangle)= 90
xz (hauteur du triangle isocele en vert*le plus grand coté du rectangle)= 5400
yz (le plus petit coté du rectangle*le plus grand coté du rectangle) = 2700
le systeme alors resolu donne :
x = 60
y = 30
z = 90
cherchant le perimetre du triangle vert, on utilise une nouvelle fois Pythagore (z/2)²+x² = w² avec w cote du triangle isocele vert
l'application numerique donne w = 75 soit le perimetre du triangle isocele : 2w + z = 240
voila ciao


 hauteur du grand triangle isocèle,Pythagore:
hauteur du grand triangle isocèle,Pythagore:
 150²-120²=90
150²-120²=90
Aire totale du champ:b*h/2=90*240/2=10800u²
Aire de la parcelle de chacun des frères:10800/4=2700u²
Soit x la longueur du rectangle
soit y la largeur du rectangle
xy=2700
aire du triangle vert=(x(90-y))/2=90x/2-xy/2
45x-xy/2=2700
or xy=2700 donc 45x-2700/2=2700
45x=4050
x=90
xy=2700
90y=2700
y=30
Donc la hauteur du traingle vert h=90-30=60
la moitié de la longueur du rectangle est égale à 45.
D'après pythagore dnas le trinagle formé par la hauteur du traingle vert,l'un des ses 2 côtés j et de la moitié de la longueur du rectangle
j= 45²+60²=75
45²+60²=75
Donc le périmètre du rectangle P=2*75+90=240


 grace a pythagore on trouve que l'aire totale du champ est de 10800m²
grace a pythagore on trouve que l'aire totale du champ est de 10800m²
il faut donc partager le champ en 4 parties de 2700m²
le seul cas permettant au rectangle et au triangle isocèle d'avoir une aire égale de 2700m² est une largeur de 30m pour le rectangle (et donc une hauteur de 60m pour le triangle) et une longueur de 90m pour le rectangle (une base de 90m pour le triangle)
avec ces dimensions, le triangle isocèle a pour périmètre : P=90+ (60²+45²)+
(60²+45²)+ (60²+45²)
(60²+45²)
P=240m
en espérant ne pas m'etre trompé


 H= hauteur du grand triangle isocèle = 90 (via Pythagore)
H= hauteur du grand triangle isocèle = 90 (via Pythagore)
Surface d'une part = (240.90/2).4=2700 m²
S(rectangle) = L.l
S(petit triangle) = L.h/2
Or, h=90-l
D'où 2.L.l = L.(90-l) <=> l=30m
D'où h= 60m et L=90m
Par ailleurs, si on note c côté du petit triangle isocèle alors h²+(L/2)² = c² d'où c=75m
Le périmètre du petit triangle isocèle est donc de 2.75+90=240m


Le périmètre de la parcelle du plus jeune est : 240 m


 le perimettre du champs du plus jeune et de 240 m
le perimettre du champs du plus jeune et de 240 m
Bravo, beaucoup de bonnes réponses.
La réponse attendue était 240 m.
Certaines réponses sont assez détaillées pour m'exempter d'explications complémentaires.

Je me suis trompé de parcelle a calculer !!! 


J'ai calculé celle en forme de faucille, l'une des deux extremes, ca revient au même et il y avait quelques calculs suplémentaires même.
Vous pouvez pas faire un petit geste ... mais je pense que ca sera 
Mais si ca pouvait être le cas, ca serait 
Je suis dégouté, mais peut importe remarque ...
Tu as bien deviné Fabien, je ne peux pas t'accorder un Smiley puisque tu n'as pas répondu à la question posée.
C'est clair que cela est du uniquement à la distraction, mais ...

Nombre de participations : 0
Temps de réponse moyen : 32:09:58.



