Challenge n°131:*:

Posté par puisea puisea

Bonjour,

Dans l'unique lycée de l'île des mathématiques, tous les élèves sont internes bien entendu. À leur arrivée, Tom_Pascal les accueille en leur disant qu'ils ne pourront accéder à l'avion qui doit les ramener dans leurs foyers aux prochaines vacances scolaires, qu'à l'aide d'un code secret. Ce code est la partie entière de la somme:



Quel est le code qui vous permettra de rentrer au bercaille ?

Bonne chance à tous !

Posté par Pookette Pookette

652 ?

Excel a eu du mal à tout calculer ...

Pookette

Posté par goupi1 (invité)

Devant m'absenter et n'ayant pas beaucoup de temps j'ai fait un rapide calcul simple qui me donne 2005 (sans garantie)

Posté par kyrandia (invité)

bonjour,

je propose le code 2004

Posté par piepalm piepalm

En découpant en n-1 intervalles [k,k+1] l'intervalle [1,n] d'intégration de la fonction 1/x on obtient les inégalités:
1/2+...+1/n<2n-2<1+1/2+...+1/(n-1)
soit 2n-2+1/n<1+1/2+...+1/n<2n-1
comme 21007000=2006,99, la partie entière cherchée est 2005

Posté par Nofutur2 Nofutur2

Je trouve 2005, sans gloire c'est à dire sans me passer de l'outil informatique.

Posté par CJ2005 (invité)

Bonjour,

Voici ma réponse : 2005 !

Salut !

Posté par philoux (invité)

Bonjour,

réponse proposée : 2005

Méthode ( ) : au bruit de calcul près d'excel...

j'attend une méthode "propre"...

Merci pour l'énigme,

Philoux

Posté par Dal (invité)

673679404 peut-être ?

Posté par Ptit_belge Ptit_belge

Bonjour,

Je trouve 2005 en utilisant les techniques de la NSA (force brute)

Posté par merrheim (invité)

Notons N=1007000
Notons S= somme(i=1 à N)1/racine(N)
Pour tout x
1/racine(x)>=racine(x+1)-2racine(x)
donc S>=racine(N+1)-2>2005

2racine(x+1)-2racine(x)+1/8xracine(x)>=1/racine(x)

donc S<=racine(N+1)-2+1/8.somme(i=1 à infini)[1/(i*racine(i))]

or somme(i=1 à infini)[1/(i*racine(i))<=1+integrale(1à infini)1/(x*racine(x))=3/8
donc
or 1/8.somme(i=1 à infini)[1/(i*racine(i))]<3/8
donc S<=racine(N+1)-2+1/3<2006
donc 2006>S>2005

La valeur recherchée est 2005

Posté par franz franz

  

Posté par jacques1313 jacques1313

2005 !

Posté par borneo borneo

Bien plus dure que celle des poules que j'ai faite en trois minutes.... bref, quand n est très grand, la somme tend vers le double de la racine du dernier terme. Je trouve 2006,99...
donc la réponse est

2006

merci pour l'énigme.

Posté par manpower manpower

Bonsoir,

La fonction étant continue, positive et décroissante sur , on a l'encadrement intégral suivant :

Ainsi,
soit .
Arff.. l'encadrement un poil trop large ne permet pas exactement de conclure, je suis (encore) allé trop vite
mais si à la place d'approximer par la méthode des rectangles on prend celle du point milieu on passera outre ce petit désagrément.

La partie entière de la somme demandée est .
(je suis peut-être passé à côté d'une évidence... une seule étoile?)

Merci pour l'énigme.

Posté par peej (invité)

Posons
Comme f est décroissante on a :



Or :



d'où

et

Or

donc

donc je dirai que selon toutes probalités, E(S)=2005 (oui je sais, c'est pas très rigoureux...)

Posté par Youpi Youpi

N'ayant pas de quoi programmer j'ai fais avec Excel et franchement c'est pas super pratique !
Et je trouve 2005.

Posté par caylus caylus

Bonsoir,

2005.

Posté par RickThomas (invité)

Bonjour

avec un programme informatique, le code secret est :

2005


Merci pour l'enigme

Posté par hervé (invité)

Merci pour ce casse tête.
J'obtiens une somme de 2005.52794.
Ainsi, le code est 2005.
A+

Posté par Nofutur2 Nofutur2

Bon sang !!! mais c'est bien sûr...J"avais oublié d'utiliser nos chères intégrales ...(ah je suis vraiment rouillé !).
L'intégrale de la fonction f(x) =1/x est égale à 2x.

En centrant les intervalles des petits rectangles de largeur 1 et de hauteur f(n), n, j'obtiens S 2(1007000,5 -0,5) = 2(1003,49 - 0,70) = 2005,58
Réponse  : 2005

Posté par geo3 geo3

Bonjour
J'ai juste employé le logiciel Derive. En tapant Sum(1/rac(n),n,1,1007000) qu'il suffit de simplifier et de choisir approximation. On peut aussi s'en sortir avec Excell pour trouver d'un côté comme de l'autre comme partie entière 2005.
A plus.

Posté par kaiser kaiser

Le code permettant de rentrer au bercaille est 2004.

Posté par chris13010 (invité)

503500

Posté par paulo paulo

bonjour,

je n'ai pas trouve de solutions tres elegantes . enfin bref

ce doit etre 2005


et comme cela correspond a l'annee en cours cela a une petite chance d'etre un resultat possiblement bon

merci et a plus tard

Paulo

Posté par Bcracker Bcracker

Bonjour,

Je trouve que le code secret est : 712056

Merci pour l'énigme

Bcracker

Posté par zackary0 (invité)

Ouf! J'ai fini de calculer la somme de avec ma calculatrice, c'était tellement long que j'ai dû changer 3 fois les piles de ma calculette ! Apres tant d'effort, je trouve , l'année mondiale de la physique.

Posté par BeauBrius (invité)

J'ai fait un petite code en php afin de me donner le resulta
mon code :

<?PHP
$r = '0'; //la variable de resulta est initialiser
for($l=1;$l<1007000;$l++) // boucle qui va se repeter jusca $l soit a 1007000
{
  $ll =(1/sqrt($l)); // $ll =
  $r = ($r + $ll ); // ajoute de $ll au resulta
}
echo floor($r) ; // affichage de la partie entier du resulta
?>
ainsi ce code va ajouté 1/racine(1) ... jusca 1/racine(1007000)

le resulta est : 2005

Posté par sebisp (invité)

2004

Posté par Tobi (invité)

2005

Posté par puisea puisea

Enigme clôturée...
Merci à tous de votre participation
Prochaine énigme entrain d'être étudiée

Posté par borneo borneo

Bonjour, y a des choses qui m'échappent... d'abord, je n'ai pas de poisson pour une mauvaise réponse, et puis il y a quelqu'un qui a le même raisonnement que moi et la même réponse et qui a bon...
Et surtout, je ne vois pas où j'ai pu me planter. Ou alors je n'ai pas compris ce qu'est une partie entière ?

Posté par borneo borneo

Oups, le même raisonnement, mais pas la même réponse. Ce qui fait que je ne comprends pas... Mais je ne suis peut-être pas bien réveillée

Posté par J-P J-P

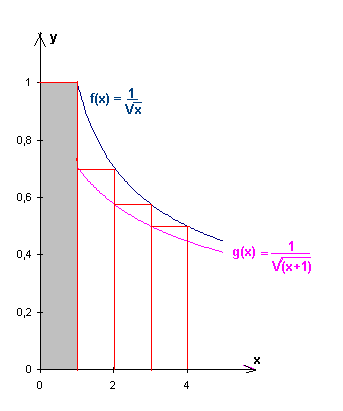
Une approche possible:

La somme cherchée est équivalente à l'aire de tous les rectangles rouges pour x jusque 1007000

Cette aire = A = aire en gris + (une aire plus petite que l'aire sous la courbe en bleu).
ce qui donne :


On a aussi A > aire en gris + (une aire plus petite que l'aire sous la courbe en mauve).
soit:



On a donc:






Donc la solution est 2005.
-----

Posté par Pookette Pookette

un poisson ...

comment excel a-t-il pu me faire faux-bond

la prochaine fois je réfléchirai un peu

Pookette

Posté par J-P J-P

Ce n'est pas Excel pookette, c'est une distraction de ta part.
Je parierais que tu as utilisé 107000 au lieu de 1007000

Remarque que pour introduire 1007000 en n'utilisant Excel qu'en simple tableur sans utiliser de la programmation Visual Basic, il fallait vraiment beaucoup de cellules.

Posté par Pookette Pookette

J-P ... J'avoue ! Je me suis trompée d'un zéro quelque part ...
en fait je suis un peu bête j'aurai pu utiliser de la programmation effectivement
une petite boucle et c'était réglé !

Merci pour ton explication en tous cas

Pookette

Posté par goupi1 (invité)

Bonjour
Dans ce challenge sympa mensuel d'énigmes à résoudre, on a aucune chance de l'emporter dès qu'on a un "poisson". Par la suite, quitte à faire faux, je réponds rapidement car de multiples tâches m'attendent par ailleurs. C'est ma philosophie. Par contre, sur les problèmes qui me semblent intéressants j'essaie d'y revenir.
Pour ce problème j'avais trouvé rapidement une formule qui est une borne supérieure à la vraie valeur.
Comme l'a fait par la suite Nofutur, il suffit d'intégrer et on remplace la somme des surfaces des rectangles par la surface sous la courbe qui passe par le milieu des faces supérieures des rectangles. Pour améliorer le résultat je suis parti après 30 car la différence entre les 2 sommes s'amortit plus n est grand. La courbe forme avec les faces supérieures des rectangles des "triangles curvilignes". Du fait de la pente de la courbe qui diminue, pour chaque rectangle, la surface du triangle curviligne supérieur est supérieure à la surface du triangle curviligne inférieur (ce qu'un calcul confirme) d'où la formule trouvée est une borne supérieure. On obtient : Borne supérieure =
Cte + 2  (n > 30)
avec Cte = ++...+ - 1,460230841
Pour notre problème cela donne 2005,52806

Après avoir envoyé ma solution, j'ai cherché une borne inférieure histoire de confirmer mon résultat et surtout histoire d'améliorer grandement le résultat. J'ai évalué en fonction de n la différence de surface des triangles curvilignes. J'ai comme dans la première étape intégré cette fonction. On obtient : Borne inférieure =
Cte + 4[(n + 1/2)^1/2 + 1/3 (n^3/2 - [n+1]^3/2)]
avec Cte = Cte précédente - 40 - 2 + 4/3 31   - 1,460354528
Pour notre problème cela donne 2005,516227

Mais la somme cherchée est beaucoup plus près de la borne inférieure que de la borne supérieure. Je pense que la somme cherchée vaut environ 2005,517 ou 2005,518. Si on continue le processus sur une seule étape on aura au moins 6 décimales exactes quelquesoit n. Impressionnant !!!

Posté par goupi1 (invité)

JP, en partant de la courbe qui passe par le milieu des faces sup des rectangles, on est d'emblée beaucoup plus précis que de faire la moyenne des 2 courbes que tu as tracée.

Posté par goupi1 (invité)

...tracées.

Posté par J-P J-P

Salut goupi1

Il n'y a aucune raison de vouloir être plus précis que les courbes que j'ai tracées si on veut juste résoudre le problème.

Ces 2 courbes permettent d'encadrer le résultat de telle manière que la solution est incontestablement 2005.

Toute précision supplémentaire est de "l'overdesign" dans le cadre du problème posé. Mais cela peut être intéressant hors cadre du problème posé.

:à

Posté par borneo borneo

Mon mon !!!!!

et surtout comprendre pourquoi je me suis plantée

Posté par J-P J-P

borneo, seul puisea auteur de l'énigme ou un webmaster peuvent te remettre ton , cela viendra sûrement.

Essaie de comprendre le dessin de ma réponse et tu verras que en comptant de "double de la racine carrée" comme du tis, tu comptes en trop une multitude de petits triangles, d'où ta réponse est trop grande.

Posté par puisea puisea

Bonjour, voila mon oubli est corrigé :s

Posté par goupi1 (invité)

Rebonjour JP
Mon étude ne concerne plus ce problème bien sûr mais l'étude en général d'une telle somme avec le plus de précision possible. Ce qui est remarquable également c'est qu'on peut l'appliquer mutatis mutandis à des sommes d'exposants quelconques.

Posté par borneo borneo

Merci... je vais essayer de comprendre. Mon approximation était... trop approximative, 1007000 n'est pas l'infini. Too bad. N'empêche que pour une énigme d'une étoile, je trouve ça salé

ps je préfère réclamer mon poisson moi-même que d'avoir les réclamation d'un autre candidat, car mieux on est classé, plus les autres sont attentifs. Normal, ce qui compte, c'est de gagner

Posté par Pookette Pookette

borneo, nous n'avons pas trouvé le code donc on va devoir rester ensemble à l' pour les prochaines vacances

Pookette

Posté par J-P J-P

Oui borneo, cette énigme aurait mérité plus qu'une étoile, je suppose que ce qui a fait hésiter puisea dans le nombre d'étoile(s) à attribuer, c'est que l'énigme pouvait être résolue avec 2 ou 3 lignes de programmation.

Si une démonstration mathématique avait été demandée, alors ...

Mais il fallait dans ce cas avoir le temps et le courage pour puisea de corriger toutes des différentes démonstrations possibles.

Posté par borneo borneo

Pookette, moi, de toute façon, je ne prends pas l'avion, j'ai trop peur... je l'ai pris très souvent, et puis d'un seul coup, la phobie. Si je décide d'aller à New York, ce sera sur le Queen Mary

J-P, pour moi, le nombre d'étoiles n'a pas vraiment d'importance, j'essaie toujours. Mais quand il y a trois étoiles et que je trouve en 5 minutes, comme la poule et les oeufs, j'ai peur de me tromper. Et quand il me faut des heures pour une seule étoile, je me dis que je vieillis !!!

Posté par Tom_Pascal Tom_Pascal

Effectivement une étoile car un bon langage de script, on peut faire une ligne de code pour obtenir le résultat :

En perl :
for ($i=1;$i<=1007000;$i++) {$nb+=1/sqrt($i)} ; print int($nb);
donne directement : 2005