Bonjour Youssouf ,
n'as tu pas oublié des parenthèses pour f(x)? réponds vite pour pouvoir t'aider.

Attention , Youssouf , f n'est pas définie pour x=1 et 3 (qui annuleraient le dénominateur ):donc ,pour le a) tes résultats sont corrects si tu précises que les intervalles ]-°°,1[ et ]3,+°°[ sont
"OUVERTS" .
b) Un max et un min donc dans l'intervalle ]1,3[ (ouvert).

Attention , j'ai dit des bétises :
il s'agit des valeurs de a ,pas de x!
tu as donc raison pour le a).

1)
a)

f(x) = (x²-ax)/(x²-4x+3)

Df: R/{1 ; 3}

f '(x) = ((2x-a)(x²-4x+3)-(2x-4)(x²-ax))/(x²-4x+3)²
f '(x) = (2x³-8x²+6x-ax²+4ax-3a-(2x³-2ax²-4x²+4ax))/(x²-4x+3)²
f '(x) = (-4x²+6x+ax²-3a)/(x²-4x+3)²
f '(x) = (x²(a-4)+6x-3a)/(x²-4x+3)²

Pour avoir des extrema dans la représentation de f(x), il faut que f(x) esite et que f '(x) = 0.

f '(x) = 0  -->
x²(a-4)+6x-3a = 0

x = (-3+/- V(9+(a-4)(3a))]/(a-4)  (V pour racine carrée)
x = (-3+/- V(9+3a²-12a)]/(a-4)
x = (-3+/- V(3a²-12a+9)]/(a-4)

Il faut donc que 3a²-12a+9 >= 0
3(a-1)(a-3) >= 0
donc a dans [-oo ; 1] U [3 ; oo[

Mais si a = 1 --> f '(x) = 0 pour x = 1 et c'est interdit --> a= 1 ne convient pas.
Et si a = 3 --> f '(x) = 0 pour x = 3 et c'est interdit --> a= 3 ne convient pas.

--> finalement  a dans [-oo ; 1[ U ]3 ; oo[ permettra des extrema pour f(x)

Et donc pour a dans [1 ; 3], f n'admet ni maximum ni minimum
-----
b)
f '(x) = (x²(a-4)+6x-3a)/(x²-4x+3)²
(x²-4x+3)² > 0 quel que soit x dans Df et donc f'(x) a le signe de x²(a-4)+6x-3a.

f '(x) = 0 pour x = (-3 +/- V(9+(a-4)(3a))]/(a-4)
x1 = (-3 - V(9+(a-4)(3a))]/(a-4)
x2 = (-3 + V(9+(a-4)(3a))]/(a-4)

f '(x) est de signe différent de part et d'autre de x1 et de part et d'autre de x2.

x1 = (-3 - V(9+(a-4)(3a))]/(a-4)
x2 = (-3 + V(9+(a-4)(3a))]/(a-4)

Si a est dans [-oo ; 1[ U ]3 ; 4[ , on a x2 < x1
f '(x) < 0 pour x dans ]-oo ; x2[ -> f(x) est décroissante.
f '(x) = 0 pour x = x2
f '(x) > 0 pour x dans ]x2 ; x1[ -> f(x) est croissante.
f '(x) = 0 pour x = x1
f '(x) < 0 pour x dans ]x1 ; 3[ -> f(x) est décroissante.
Il y a un minimum de f(x) pour x = x2
Il y a un maximum de f(x) pour x = x1

Si a est dans ]4 ; oo[ , on a x2 > x1
f '(x) > 0 pour x dans ]-oo ; x1[ -> f(x) est croissante.
f '(x) = 0 pour x = x1
f '(x) < 0 pour x dans ]x1 ; x2[ -> f(x) est décroissante.
f '(x) = 0 pour x = x2
f '(x) > 0 pour x dans ]x1 ; 3[ -> f(x) est croissante.
Il y a un maximum de f(x) pour x = x1
Il y a un minimum de f(x) pour x = x2

Donc pour a dans [-oo ; 1[ U ]3 ; 4[ U ]4 ; oo[, f a un max et un min.

Il reste à montrer que M et m ont les mêmes signes et donc que Mm > 0
(Je n'ai pas le courage de le faire)
-----
c)
f '(x) = (x²(a-4)+6x-3a)/(x²-4x+3)²

Si a = 4, on a:
f '(x) ne s'annule que pour 1 et 1 seule valeur de x qui est x = 2.

Dans Df:
f '(x) < 0 pour x < 2
f '(x) = 0 pour x = 2
f '(x) > 0 pour x > 2

Il y a donc un minimum de f(x) pour x = 2.

Il y a un minimum seul pour f(x) pour a = 4
-----
Sauf distraction. Vérifie.  

--> finalement a dans [-oo ; 1[ U ]3 ; oo[ permettra des extrema pour f(x)

Et donc pour a dans [1 ; 3], f n'admet ni maximum ni minimum

Tout le monde semble oublier un truc.
Ok, dans [1,3] il n'y a pas d'extremum, mais qui dit qu'il y,en aura ailleurs?

Bonjour,

Il est bon de remarquer aussi que :
a=1 f(x)=x(x-1)/(x-1)(x-3) = x/(x-3) point A(1;-1/2) exclus
a=3 f(x)=x(x-3)/(x-1)(x-3) = x/(x-1) point B(3;3/2) exclus

Est-ce celà que Otto veut dire ?

Par ailleurs, la famille de courbes paramétrées ci-dessous montre le cas a=3,5 présentant aussi un minimum seul...

Philoux

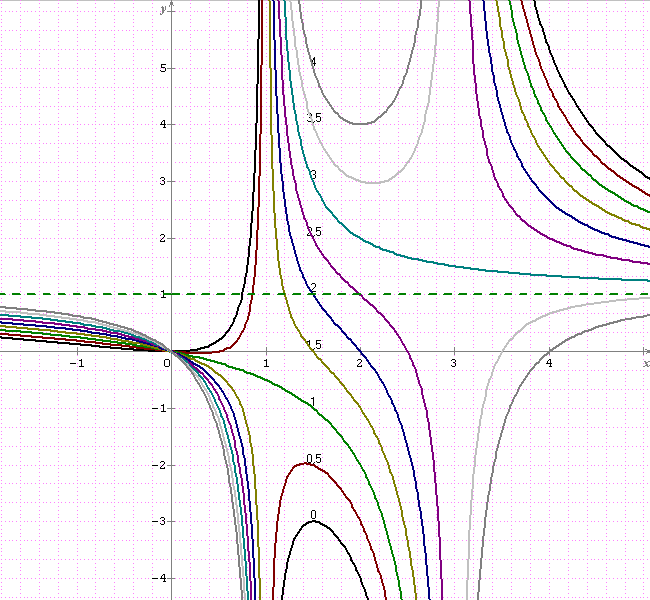
Otto

Il me semblait que ma réponse montrait sans ambiguïté l'existence d'extrema en dehors de [1 ; 3] et même pour quelles abscisses ils existaient et aussi leur type (max ou min).

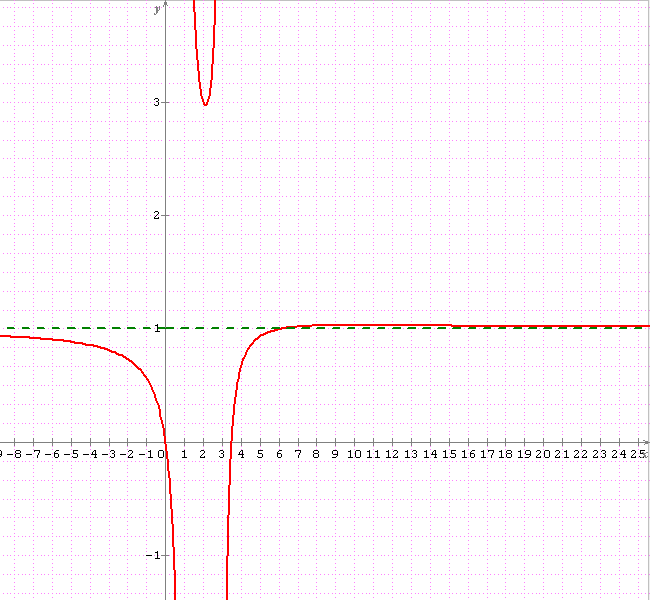
Non philoux, pour a = 3,5 , on a:

Un minimum de f pour x = 2,12701665379
et un maximum de f pour x = 9,87298334621.

Le maximum n'est peut-être pas très marqué, mais il existe bel et bien.
-----
Les graphes, c'est bien mais attention aux échelles.

Bien vu J-P

J'avais pas envisagé que la courbe coupait son asymptote y=1...

En image, pour a=3,5

Philoux

bein je vous remerci vous tous

Est-ce celà que Otto veut dire ?
Non, ce que je veux dire c'est que l'on enlève les valeurs ou f'(x)=0 possède une solution. (sauf si j'ai mal compris)
Mais le fait que f'(x)=0 n'implique pas que f admette un extremum...

tu as raison otto le fait que f'(x)=o n'implique pas que f admette un extremun mais c'est  une condition necessaire pour avoir un extremun