Inscription / Connexion Nouveau Sujet
aire d'un triangle
Bonjour
Je dois calculer l'aire d'un triangle ABC sachant que :
- Périmètre (ABC) = 9.5cm
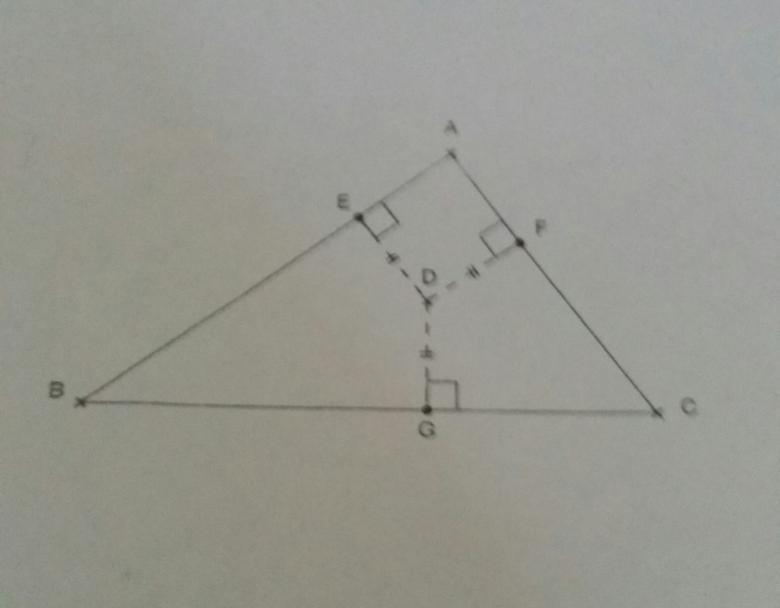
- Il y a un point D (d'après la figure dans le triangle) tel que DE=DF=DG=1.8cm, E, F, G étant des points des côtés du triangle ABC, respectivement AB, BC, AC avec (DE)perpendiculaire à (AB), (DF) perpendiculaire à (BC), (DG) perpendiculaire à (AC).
J'ai essayé d'utiliser A(triangle) = c x h/2 mais je n'ai ni de hauteur ni un coté...
J'ai essayé de partir du périmètre AB+BC+AC = 9.5cm mais je ne vois pas quoi en faire
J'ai essayé de prouver que le triangle ABC était rectangle mais rien de moins sûr.
Je n'ai pas de mesure d'angle (à part les angles droits) donc je ne peux pas utiliser la trigonométrie.
Pas de parallèle pour utiliser Thalès
Merci d'avance pour les pistes de réflexion que vous pourriez me donner pour me décoincer.
Bonjour,
L'aire demandée est égale à l'aire de trois triangles/:
Joignons BD et DC. L'aire du triangle BDC = (1,8 *BC)/2
Joignons DA. L'aire du triangle CDA = (1,8*AC)/2
L'aire du triangle ADB = (1,8*AB)/2
L'aire demandée =(1,8*BC)/2 + (1,8*AC)/2 + (1*8*AB)/2 =
L'aire demandée = 1,8*(BC+AC+AB)/2 c'est-à-dire ( 1,8*périmètre)/2
(1,8 *9,5)/2
Annuler
connectez vous