Inscription / Connexion Nouveau Sujet
calcul d'aire
Abdou874
aider moi à trouver l'aire de la portion indiquée sur cette figure.Merci
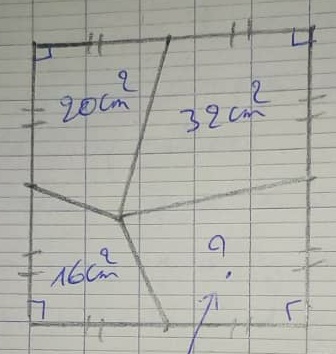
Bonjour,
Commence par déterminer la longueur du côté de ce carré.
Une fois que tu auras trouvé, trouver l'aire qui te manque ne posera plus aucun souci.
Bonjour à toi aussi
Bien qu'inscrit en décembre 2018, je me demande si tu as pris la peine de consulter A LIRE AVANT DE POSTER. Merci.
Tu dois écrire ton énoncé textuellement et en entier.
Le problème est que il n'y a aucune donnée a part les aires des différentes portions,avec ces données c'est presque impossible de trouver la mesure d'un côté.
la FAQ du forum
équivalences des systèmes de niveaux scolaires
Bonjour
Après la question reste quand même vague...
Car plusieurs solutions sont possibles...
elle est précise et il n'y a qu'une seule solution et il ne manque aucune donnée,
maintenant est elle du niveau ??
c'est uniquement sur la formule de l'aire d'un triangle, et du calcul tout en littéral
rien d'autre.
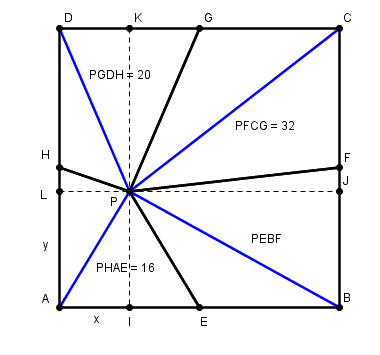
j'appelle c le côté du carré
x la distance de P au coté AD
y la distance de P au coté AB
ainsi l'aire de PHAE = aire de PHA + aire de PAE = 1/4 cx + 1/4 cy = 16
et pareil pour PFCG et PGDH
en moulinant ces 3 égalités, on trouve la 4ème (celle de l'aire de PEBF)
et comme résultat annexe, la mesure unique du côté du carré et la position unique du point P (les valeurs de x et y)
normal :
3 inconnues c, x, y et 3 équations : les 3 aires données.
la figure Geogebra a été faite avec ces valeurs là des dimensions, et les valeurs affichées par Geogebra des aires confirment
(pour ne pas déflorer la recherche, l'aire de PEBF n'a pas été affichée)
Nota :
le moulinage des expressions littérales conduit à démontrer que l'aire coloriée est toujours égale à la moitié de l'aire du carré quel que soit la position de P
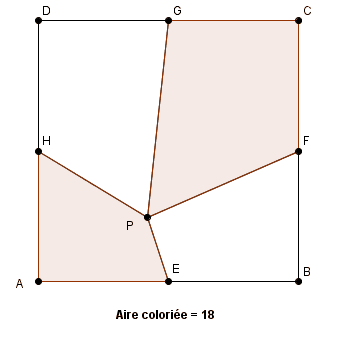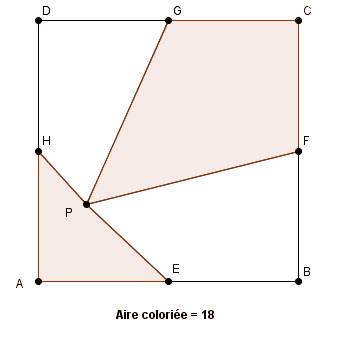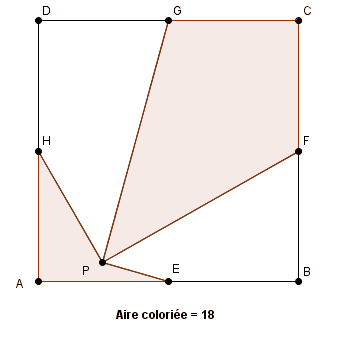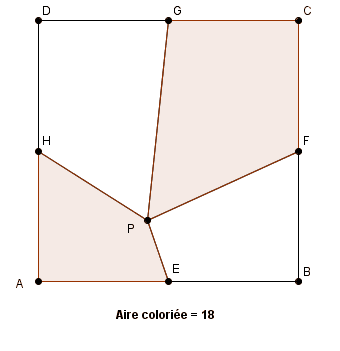
ce résultat remarquable (bien entendu il faut le démontrer !!) doit sans doute pouvoir être démontré autrement que pas des relations algébriques !
doit sans doute pouvoir être démontré autrement que pas des relations algébriques !
sur la 1ère figure on remarque sans aucun calcul que l'aire de PAE =aire de PEB
etc
en découpant ainsi le carré en 8 triangles et en les regroupant ainsi par paires on aboutit instantanément au résultat remarquable cité.
dont la solution de l'exo découle en une demi ligne.
sans avoir besoin d'invoquer un quelconque calcul du côté du carré, et encore moins de la position de P
Bonjour,
avec d'autres triangles, et sauf erreur !
Aire HPGD= aire HGD + aire HPG
Aire
Aire EBFP= aire EBF + aire EFP
Aire
Aires
Aires = moitié aire du carré ABCD
de même
Aires = moitié aire du carré
d'où l'égalité des aires
si x est l'aire cherchée 20+x = 16 + 32 soit x= 28 cm2
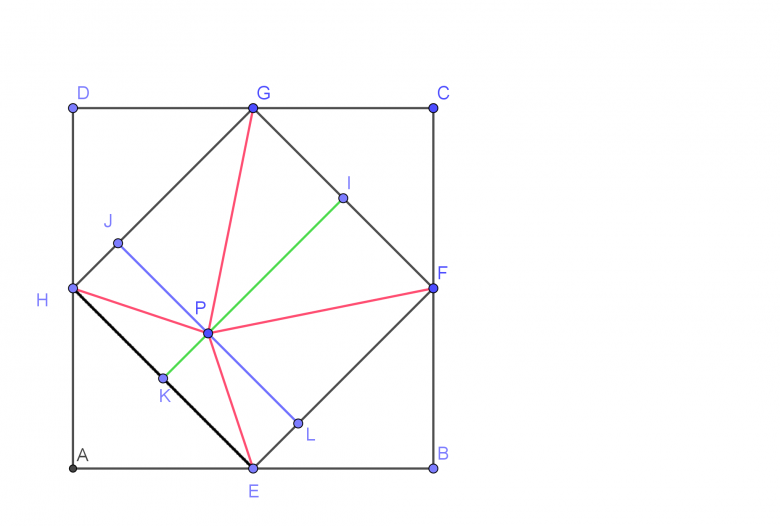
On peut effectivement aussi découper comme ça mais
• laisser le demandeur faire les calculs effectifs était plus dans l'esprit du forum
• il me semble plus naturel de justifier que cette aire rouge est une certaine fraction de l'aire du carré, indépendante de la position de P :
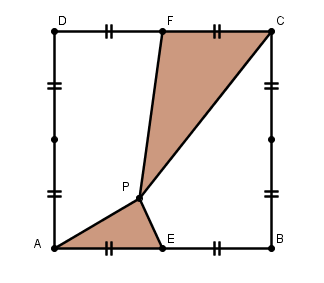
et tout le reste en découle "immédiatement" sans invoquer des racines carrées de quoi que ce soit.
mathafou
laisser le demandeur faire les calculs effectifs était plus dans l'esprit du forum
tout le reste en découle "immédiatement" sans invoquer des racines carrées de quoi que ce soit.
mais en mettant les hauteurs et les bases parallèles aux côtés du carré, il n'y a même pas d'hypoténuses, c'est ce que je voulais dire.
Annuler
connectez vous