Inscription / Connexion Nouveau Sujet
calcul d'angle et de surface dans un cercle
Bonjours,
c'st un problème de symétrie d'un cercle par rapport à une de ses cordes DB.
c'est pour un peut mieux comprendre pi et le segment.
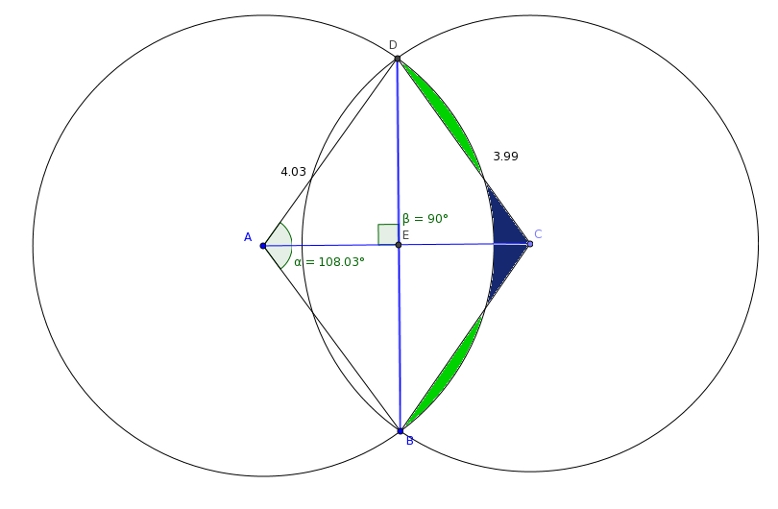
quel est l'angle α nécessaire pour que la surface verte et la surface bleu soit les même?
j'avais trouvé 108 à 115 par la mesure des pixels mais es ce que cela peut avoir un rapport avec un pentagone?
Merci
En effet, il y a bien une ressemblance avec sin(x) et x/2 sur le graphe de cet exercice.
https://www.ilemaths.net/sujet-objectif-resoudre-l-equation-e-sin-10-x-2-330051.html
j'aurais peut être due commencer par demander comment calculer les surfaces en fonction du rayon?
Je ne comprends pas ce que tu dis à propos de la "ressemblance".
Par ailleurs, il n'y a pas besoin de calculer les surfaces bleues et vertes.
Indication : il suffit de comparer l'aire du losange avec l'aire du secteur de disque. Ceci conduit à l'équation .
je parle de "ressemblance", x=2sin x =108.6038216°
je m'attendais vraiment pas avoir une réponse en trigonométrie.
c'est surement en utilisant les propriétés du losange et dans mon esprit cela ne reste qu'un arc de cercle et deux rayons contrairement a ce qui est déssiné, c'est possible.
en ce qui concerne les surfaces:
aire du losange= Aire secteur -vert+ bleu et comme vert et bleu sont egaux donc
aire du losange= Aire du secteur
le problème reste de savoir quand vert et bleu sont égaux.
Merci pour ta patience.
ça ferra pas de mal
R*
donne la longueur de l'arc de cercle
R**R /2 donne l'aire du secteur
pour l'aire du losange le théorème est d*D/2 mais ça ne m'arrange pas, je préférerais l'équation R² avec un facteur de transformation corespondant à l'angle
peut être que comme cela et je comprend personnellement mieux A=pi R² ou P=2piR
donc le losange c'est ce même carré mais transformé
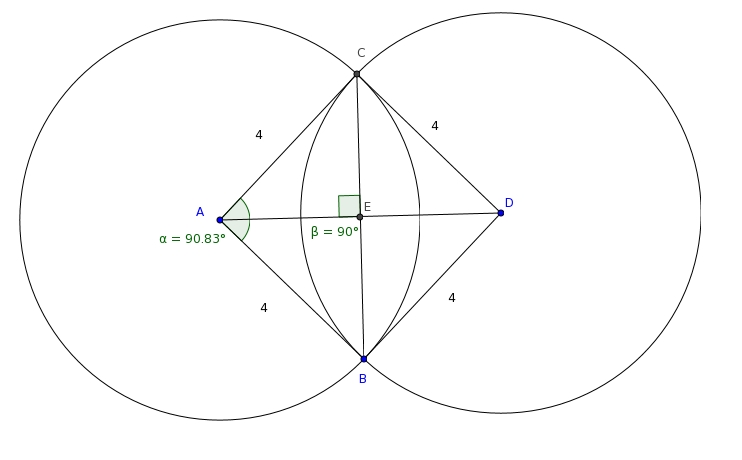
Vraiment, tu ne veux pas exprimer l'aire du losange en fonction de et de fonctions trigonométriques de
? C'est pourtant ultra-simple, je t'assure !
Bonjour.
Soit x l'angle ADC.
L'angle tangentiel qui sous-tend un arc vert est (pi/2)-(pi-2x) = 2x-(pi/2) et l'arc est 4x-pi..
Une zone verte mesure (4x-pi)/2pi - sin(4x-pi).
La moitié de l'arc bleu mesure x-(4x-pi) = pi-3x.
F étant le point de contact entre la zone bleue et une zone verte, l'aire du triangle ACF est cos(x).sin(pi-3x).
La moitié de la zone bleue mesure : cos(x).sin(pi-3x)-(pi-3x)/2pi.
x/2pi = cos(x).sin(pi-3x)+sin(4x-pi)
x 
0,957845808110279 radians 54,8805222290167 degrés
C'est incompatible avec la réponse 108.6038216° pour l'angle (la somme des deux doit faire 180°).
Et j'ai plutôt confiance en mon résultat.
Bonjour,
par la mesure des pixels
la figure initiale étant fausse (les deux cercles ne sont pas égaux) une telle "mesure des pixels" ne veut pas dire grand chose. il est vrai que de 108 à 115° il y a de la marge !
comme dit par GaBuZoMeu, et en partant d'une figure juste ça sera mieux, aucune des figure de godzylla n'étant représentative (la meillere est encore la première !), la condition est que l'aire du segment de cercle soit égale à celle du demi losange :
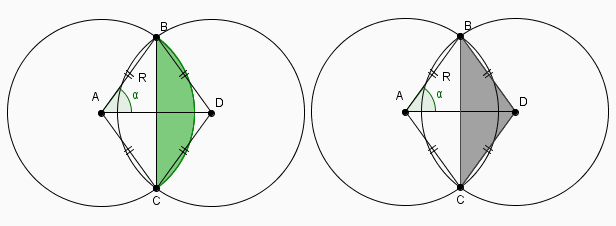
l'aire du segment étant l'aire du secteur moins ... précisément l'aire du demi-losange ! on aboutit à la condition, simple à écrire en fonction de
:
aire du secteur ABC = 2 * aire du triangle BCD
ou encore aire du secteur ABC = aire du losange ABDC
soit R²
= R² sin(2)
et l'équation
= sin(2) dont la solution, autre que 0, (approchée, c'est une équation transcendante) est bien
0.947747... radians me dit le solveur de Geogebra.
soit
= 54.3019... degrés
et donc 2
= 108.6038°PS : ça n'a donc aucun rapport avec un pentagone (régulier) qui donne des angles de 108.0 degrés
(à moins que "en mesurant les pixels", à quelques pixels près en plus ou en moins tu confondes l'angle de 108.6° avec l'angle de 108.0°)
pour la deuxième figure, j'ai été demandé sur le site http://www.les-mathematiques.net/ comment l'aire du losange pouvais se calculer en rapport d'aire de carré.ils sont dur, ils ont tendance à attaquer celui qui posent les question pour ne pas a avoir à répondre( snobisme).
en tout cas ils n'ont pas vu le problème de topologie et l'on m'a répondu que AB²*sin (α) étais bien l'équation permettant de chiffrer l'aire du losange.
Bonjours, mathafou , merci de venir participer à cette discussion.
sin(108,6)=0.947747
54 est différent de 0,94
donc ce n'est pas la solution α=sin (2α)
C'est peut être une figure géométrique expliquant l'utilisation de la trigonométrie dans un triangle rectangle.
sinus α = opposé / hypoténuse
il faut que je prennent le temps d'y repenser.
tu sais que dans la formule donnant l'aire du secteur, est exprimée en radians, pas en degrés ???
aire d'un secteur d'angle 
est (1/2)R²,
en radians (et avec = 2
radians cela donne le disque complet (1/2)R²*2 = R²)
ici = 2 (mon , celui de GaBuZoMeu c'est ici , mais le calcul est le même, et le résultat aussi)
54 degrés est bien égal à 0.94 radians
(je te passe les décimales qui sont exactes, ce n'est pas 54° mais 54.3019...)
@godzylla : vu la façon dont tu es intervenu ici 
sous le pseudo de Zosma, rien d'étonnant à ce que tu te sois fait rembarrer !
Bonjour à tous,
>>>godzylla
tu marque dans ton profil : "doctorat"
pouvons-nous savoir dans quelle spécialité ?
Merci pour la réponse édifiante
Amitiés
Je reviens car j'ai fait une faute de français dans mon texte précédent: il faut lire "tu marques"
Bien à vous
je comprend que pour vous ce soit limpide, j'en suis très heureux pour vous.
il va falloir que je trouve la relation entre
l'aire de l'arc de cercle par rapport aux deux rayons (positif et négatif)
et P/2R
peut être comme cela l'angle va varier et aussi la valeur positive ou négative de vert- bleu.
@castoriginal: comme tu ne peut m'obliger à répondre à une question, tu risques de ne pas pouvoir deviner.
les doctorats doivent oublier tout ce qui est enseigné avant bac+5.
>>> godzylla
merci beaucoup pour ta réponse à mon message.
Continuons, je pense que l'on va bien s'amuser ensemble. J'invite également à notre fiesta les spécialistes en maths que sont GaBuZoMeu et mathafou.
Il va y avoir de l'ambiance !
Cela deviens un dossier , je rajoute donc une vidéo explicitant un peut mieux les questions précédentes.
http://www.youtube.com/watch?v=ipGeKg5EM20
Une telle "explicitation" était inutile telle que.
Si encore tu avais affiché les valeurs des aires au cours de l'animation...
en plus de ça il n'y a plus de "dossier" le problème est résolu, terminé, fini. On t'a donné la mise en équation (niveau collège, si, si)
et la résolution de l'équation x = sin(2x) ne peut se faire que de façon numérique.
Il n'existe aucune expression explicite de la solution sous forme x = valeur exacte, avec valeur ne faisant intervenir que des fonctions usuelles (de celles qu'on enseigne à l'école)
si tu veux absolument une valeur exacte, elle fait intervenir la fonction LambertW sur des nombres complexes. Aucun intérêt pratique.
Enfin pour le fun une construction "exacte" avec Geogebra :
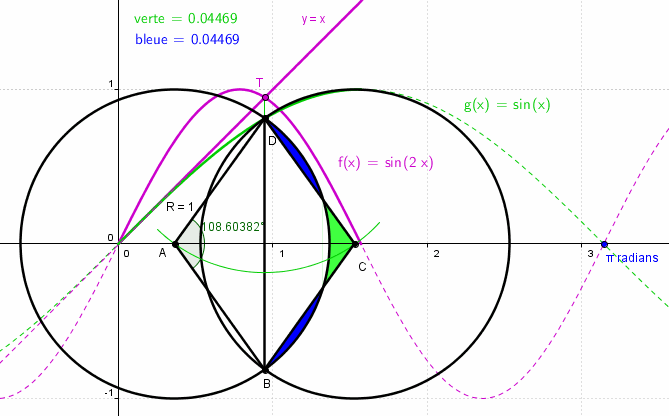
on "construit" l'intersection de la courbe y = f(x) = sin(2x) et de la droite y = x
(résolution de l'équation x = sin(2x))
qui donne le point T, d'abscise 0.94775 radians
on "calcule" sin(x) par renvoi sur la courbe g(x) = sin(x) ce qui donne le point D
le cercle de rayon R = 1 de centre D coupe l'axe des abscisses en A et C cherchés
On termine la figure avec les cercles de centres A et C, le losange et la "peinture" des aires bleues et vertes
On fait calculer et afficher par Geogebra les aires bleues et vertes
Finito.
Ici les rayons des cercles sont choisis = 1, ce qui n'a aucune espèce d'importance, si tu veux un rayon de 4, il suffit de modifier le tracé de y = sin(x) (courbe en vert) en y = 4sin(x) et de tracer le cercle de centre le point D obtenu et de rayon 4 au lieu de 1.
(à moins que tu ne penses que la valeur de dépend du rayon du cercle, ce qui ne m'étonnerait pas plus que ça de ta part)
merci beaucoup mathafou ,tu te débrouilles bien en mathématiques.
peut tu me mettre le .ggb sur http://www.geogebratube.org/ et me dire l'adresse. je n'est pas la meme version de geogébra et je ne pouvais pas réaliser la figure aussi bien que toi. c'est l'idéale.
Ensuite je ne contredit pas le fait que y = f(x) = sin(2x) , mais j'ai simplement l'impression que cette équation réduit en partis l'étendu du problème qui concerne les surfaces.
Je redemanderais dans 3 ans si tu veut mais pour l'instant, j'ai cette impression de calculer la vitesse une voiture quand se pose la question de son prix.
je n'ai pas de compte là bas pour y mettre mon ggb
il est "assez compliqué" parce qu'il y a pas mal de trucs planqués pour faire la peinture et le calcul des aires : le problème n'est pas la version de Geogebra mais l'habileté à lui faire faire des choses bizarres, les fonctions utilisées sont "des fonctions de base" dans Geogebra, même les vieux Geogebra. (de toute façon si tu en as un vieux il vaut mieux le mettre à jour !! c'est évident)
quant à
mais j'ai simplement l'impression que cette équation réduit en partis l'étendu du problème qui concerne les surfaces.
la démonstration du pourquoi de cette équation à partir justement des aires est dans les posts précédents, y compris même le tien quand tu écris :
en ce qui concerne les surfaces:
aire du losange= Aire secteur -vert+ bleu et comme vert et bleu sont egaux donc
aire du losange= Aire du secteur
le problème reste de savoir quand vert et bleu sont égaux.
aires vertes et bleues sont égales si et seulement si aire losange = aire secteur.
et aire losange = aire secteur si et seulement si l'angle (en radians) satisfait à l'équation.
pour sin(x) il faudra que soit des vecteurs ce doit être un cercle identité? et utiliser les complexes. donc peut etre f(x)=j*sin(x)
soit aire bleu appelé B
soit aire verte appelé V
soit l'angle DAB appelé α
quand 2B=V quel est la valeur de α?
Vous pouvez utiliser simplement l'équation y=sin(x)
@mathafou : ça te va comme question?
vecteurs, cercles identité, complexes, et puis quoi encore ??
ailleurs homéomorphisme, cercle qui est :
le carré symbolise l'ordre et le rond les sentiments, à un moment l'Humain leur associai(t) des éléments.
le segment e(s)t un symbole phallique qui symbolise la puissance, il a été remplacé par le vecteur.
Continues à délirer, tout a été dit et redit sur le sujet.
le calcul des aires est du niveau troisième, voire même 4ème (collège) point barre.
Rajouter là dedans des borborigmes est une perte de temps pure et simple. Apprends juste à penser
sans espoir ? au lieu de baratiner.montre un de tes trucs en mathématématiques.
j'ai plus de compte sur sitededébile.com, ils sont juste bon à réciter leur cours et à s'expliquer de travailler pour l’état sans être utile.
pose une question de géométrie de toi.
Edit jamo : insulte censurée.
Bonsoir,
>>>godzilla
tu es un peu gonflé quand tu dis " mathafou,tu te débrouilles bien en mathématiques."
As-tu conscience que tu parles à un vrai professionnel des mathématiques ? Va voir sur son site : je crois que tu en seras décoiffé !
Amitiés
si pi etais un nombre entier tu aurais surement vrai mai non donc utiliser sinus reviens mesurer sur la figure.
godzylla >> Que tu n'aimes pas le forum lesmathematiques.net est ton droit, mais les injurier et tenir des propos totalement déplacés envers eux, ça tu n'as pas le droit de le faire.
Te voilà exclu pour quelques jours du forum pour réfléchir.
D'ailleurs, tu avais déjà été exclu du forum pour un motif similaire, donc la durée d'exclusion est augmentée.
Annuler
connectez vous