S'il vous plais j'aurais besoin d'aide ...

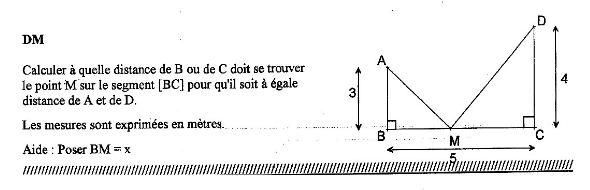
Bonsoir
Problème déjà traité ici
Va en haut à droite et cliques sur la loupe, puis tapes fontaine entre 2 tours niveau collège 3 ème, tu auras des solutions

Merci j'ai regardé mais les exercices ne correspondent pas totalement

Une aide de ta part ou d'une autre personne serait sympatique

Merci

Allez s'il vous plait je voudrais bien des réponses normalement vous etes efficaces u_u

On veut que AM=DM
Ce n'est pourtant pas très compliqué, il suffit d'appliquer le théorème de Pythagore aux triangles rectangles ABM et CDM
Dans ABM
AM²=AB²+MB²=3²+MB²=9+MB² =MB²+9(1)
Dans CDM
MD²=CD²+MC²=4²+MC²
Pour éliminer une inconnue, on exprime MC en fonction de MB
MC=BC-MB=5-MB, on a ainsi plus qu'une seule inconnue MB
Donc MD²=4²+(5-MB)²
(5-MB)² identité remarquable de type (a-b)²=a²-2ab+b²
(5-MB)²=25-10MB+MB²
MD²=16+25-10MB+MB²=41-10MB+MB²=MB²-10MB+41 (2)
Si AM=MD, on écrit (1)=(2) soit
MB²+9=MB²-10MB+41 les termes en MB² s'annulent, il reste
9=-10MB+41 ou 10MB=41-9=32
et MB=32/10=3,2 m
Je pense que tu sauras trouver MD
Vérifies avec
AM²=AB²+MB²=3²+3,2²=9+10,24=19,24 et AM=√19,24=4,38 m
AM²=AB²+MB²= ?

A enfin


Merci beucoup de ton aide car je n'avais pas tres bien compris


A bientot

De rien, si tu as compris maintenant c'est l'essentiel

Je répond au complet:[/u]

J'utilise le thm de Pythagore pour prouver que AM=MD

Pour cela, je vais l'appliquer aux triangles rectangles ABM et CDM sachant que BM=x.

Pour le triangle ABM je peux écrire AM²=AB²+BM²
                                                    AM²=AB²+x²

Pour le triangle CDM je peux écrire DM²=DC²+MC²
                                                    DM²=DC²+(BC-BM)²
                                                    DM²=DC²+(BC-x)²

Je relie ces deux équations:

AB²+x²=DC²+(BC-x)²
  3²+x²=4²+(5-x)²
  3²+x²=4²+(5²-10x+x²)
9+x²=16+25-10x+x²
9=41-10x
-10x=-41+9
-10x=-32
x=32/10
x=3.2

Sachant que x=BM, je peux dire que BM =3.2m et que CM =1.8m

Maintenant avec ces 2 mesures, je vérifie que AM=DM

Dans le triangle ABM rectangle en B, d'apres le thm de Pythagore on a :
AM²=AB²+BM²
      =3²+3.2²=9+10.24=19.24
Comme AM0 alors on a 19.244.38

Dans le triangle DCM rectangle en C, d'apres le thm de Pythagore on a :
DM²=DC²+MC²
     =4²+1.8²=16+3.24=19.24
Comme DM0 alors on a 19.244.38

Je viens de vérifier que si le point M se trouve a 3.2m du point B et à 1.8m du point C alors il sera bien à égale distance du ppint A et du point D c'est a dire à 4.38m

Et puis c'est tout ,c'est res court