Inscription / Connexion Nouveau Sujet
calculer la probabilité
bonsoir
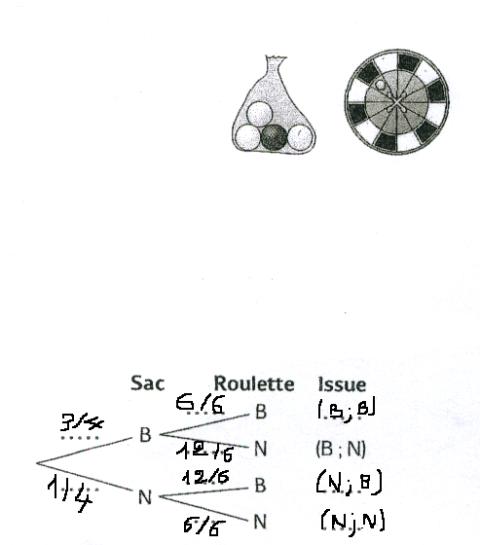
Un sac contient trois boules blanches et une boule noire.Une roulette comporte six cases blanches et six cases noires.On tire au hasard une boule du sac et on note sa couleur.Puis on lance au hasard cette boule sur la roulette et on note la couleur de la case sur laquelle elle s'arrête. Par exemple l'issue (B;N) signifie que l'on a lancé une boule blanche et qu'elle s'est arrêtée sur une case noire.
a)Compléter cet arbre des possibles et indiquer la probabilité correspondante sur chaque branche.
b)Calculer la probabilité de chaque issue.
c)Calculer la probabilité que la boule tirée s'arrête sur une case de même couleur que la boule.
mes reponses:
a)arbre compléter
b)P(B;B)=3/4*6/6= 3/4
P(B;N)=3/4*12/6= 3/2
P(N;B)=1/4*12/6= 1/2
P(N;N)=1/4*6/6= 1/4
c)P(N;N)=1-6/6=0
Bonsoir je ne comprends pas très bien ce que tu attends de nous. Tu veux qu'on te dise si tes résultats sont justes ? Car si tu penses qu'ils sont justes je ne vois pas l'intérêt de venir poster ton exercice.
je poste ceci car comme je ne suis pas sur que cela est correct car la leçon sur les probabilités j ai pas tous compris
donc est ce que mon exercice est correct car pour la question c) je ne suis pas sur merci
Bonsoir Camille.
La probabilité que la boule s'arrête sur une case blanche est 6/12, car il y a six cases blanches sur douze.
La probabilité qu'elle s'arrête sur une case noire est également 6/12.
Il faut rectifier en conséquence les fractions sur les branches secondaires de l'arbre et les fractions à droite des signes * dans les calculs.
3) P(BB) + P(NN)
On peut aussi répondre directement 1/2 car quelle que soit la couleur de la boule tirée, il y a une probabilité de 6/12 qu'elle s'arrête sur une couleur de la même couleur.


