Inscription / Connexion Nouveau Sujet
Carré excel
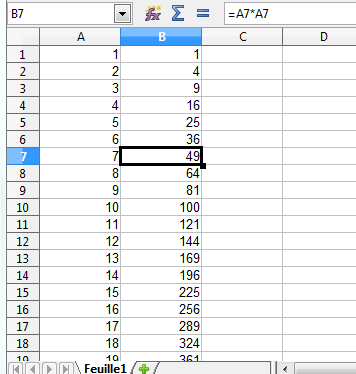
Je voudrais savoir quelle formule je dois rentrer dans B1 pour n'avoir qu'à "tirer" vers le bas et obtenir ce que j'ai commencé à écrire manuellement
Merci d'avance 
Bonjour,
j'ai le même exercice à faire et j'ai bien compris pour la colonne B, mais on nous demande quelle formule doit-on entrer en E12 pour obtenir la valeur en S(20) (qui se trouve en D15), sachant que S(n)= 1/(n^3)*(1²+2²+...+n²).
Merci d'avance de votre aide 
Justement, en E12, je n'ai rien et en D15, j'ai S(20)=?
Le but est de trouver quelle formule entrer en E12 pour obtenir la valeur de de S(20), mais je ne vois pas du tout comment faire..
Bonjour, j'ai eu cette même exercice à faire et on nous demande d'écrire un algorithme permettant d'obtenir en sortie une valeur approchée de l'aire, a partir de l'entrée n du nombre de subdivisions de l'intervalle [0;1] pour S(500) et S(1000).
Merci d'avance 
Alors on sait aussi que Sn est la somme des aires des rectangles que l'on obtient en divisant l'intervalle [0;1] en n intervalles de même longueur.
l'aire de ces rectangles peut être rapprochée par Sn et cette approximation est d'autant plus précise que n sera grand 
j'ai une longueur pour le rectangle il en manque encore une
ou quelle est la fonction pour laquelle vous voulez calculer l'aire du domaine délimité par la courbe , l'axe des abscisses, les droites x=0 et x=1 ?
On sait juste que Sn: (1/n^3)*(1²+2²+...+n²) et avec tout ça il faut écrire un algorithme pour calculer S500 et S1000 mais je ne vois pas du tout comment..
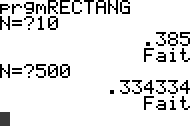
Oui vous avez raison, en fait plus le n.est grand plus le resultat se rapproche de 0.3333 (1/3) non? 
Bonsoir,
Le programme de hekla n'est pas judicieux, il fait n-1 calculs pour rien.
Je propose (à tester)
PROGRAM:RECTANG
: Promt N
: 0->S
: For (I,1,N)
: I^2+S->S
: End
: S/N^3->S
: Disp S
ou
à condition démontrer la formule :
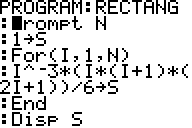
PROGRAM:RECTANG
: Prompt N
: N^(-3)*N*(N+1)*(2N+1)/6->S
: Disp S
Comment je fais pour programmer ce programme sur casio ? Puisque les manip' ne sont pas identiques ...
Bonjour
Quelle Casio ?
Pour le modèle le plus élémentaire
?->N exe
0-> S exe
For 1->I to N exe
I^2+S->S exe
next exe
S/N^3->S exe
pour le premier programme de Chatof
pour le second
?->N exe
N^(-3)*N*(N+1)*(2N+1)/6-> S exe
S(n) étant une somme de Riemann, il s'agit de la parabole, entre les verticales d'équations x=0 et x=1....